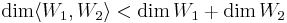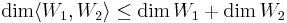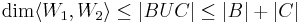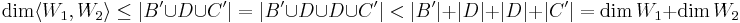Szerkesztő:Mozo/Linalg gyakorló 1.
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Alterek) |
||
| 12. sor: | 12. sor: | ||
:<math>\dim \langle W_1,W_2 \rangle \leq \dim W_1 +\dim W_2</math> | :<math>\dim \langle W_1,W_2 \rangle \leq \dim W_1 +\dim W_2</math> | ||
ha B bázis <math>W_1</math>-ben és C bázis <math>W_2</math>-ben BUC generátorrendszere <math>\langle W_1,W_2 \rangle</math>-nek, de nem nagyobb a számossága, mint |B|+|C| | ha B bázis <math>W_1</math>-ben és C bázis <math>W_2</math>-ben BUC generátorrendszere <math>\langle W_1,W_2 \rangle</math>-nek, de nem nagyobb a számossága, mint |B|+|C| | ||
| − | :<math>\dim\langle W_1,W_2\leq |BUC|\leq |B|+|C|</math> | + | :<math>\dim\langle W_1,W_2\rangle\leq |BUC|\leq |B|+|C|</math> |
| − | Most belátjuk, a szigorú egyenlőtlenséget. <math>W_1</math>∩<math>W_2</math> altér mindkét altérben, ezért ha a metszet nem 0, akkor egy D ⊆ <math>W_1</math>∩<math>W_2</math> bázis kiegészíthető <math>W_1</math> bázisává és <math>W_2</math> bázisává, | + | Most belátjuk, a szigorú egyenlőtlenséget. <math>W_1</math>∩<math>W_2</math> altér mindkét altérben, ezért ha a metszet nem 0, akkor egy D ⊆ <math>W_1</math>∩<math>W_2</math> bázis kiegészíthető <math>W_1</math> bázisává és <math>W_2</math> bázisává: B'UD és DUC'-vel. Feltehető, hogy B' elemei különböznek C' elemeitől, mert ha nem, akkor különbözőkkémeg nyújthatók. |
| − | :<math>\dim \langle W_1,W_2 \rangle\leq|B'\cup D\cup C'|=|B'\cup D\cup D\cup C'|<|B' | + | :<math>\dim \langle W_1,W_2 \rangle\leq|B'\cup D\cup C'|=|B'\cup D\cup D\cup C'|<|B'|+|D|+|D|+|C'|=\dim W_1 +\dim W_2</math> |
hiszen D elemeit kétszer számoltuk. | hiszen D elemeit kétszer számoltuk. | ||
A lap 2009. március 12., 18:33-kori változata
Alterek
1. Igazolja, hogy ha W1 és W2 altér V-ben, akkor
altér
Ugyanis, ha u,v ∈ W1∩W2, akkor u,v ∈W1 és u,v ∈ W2, de ezek zártak az összeadásra és a számmal való szorzásra, ezért: u+v ∈ W1 és u+v ∈ W2,, azaz u+v ∈ W1∩W2 és λ.u ∈ W1 és λ.u ∈ W2, azaz λ.u∈ W1∩W2,.
2. Igazoljuk, hogy ha W1 és W2 altér V-ben és W1∩W2, ≠ {0}, akkor
Először belátjuk, hogy
ha B bázis W1-ben és C bázis W2-ben BUC generátorrendszere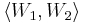 
-nek, de nem nagyobb a számossága, mint |B|+|C|
Most belátjuk, a szigorú egyenlőtlenséget. W1∩W2 altér mindkét altérben, ezért ha a metszet nem 0, akkor egy D ⊆ W1∩W2 bázis kiegészíthető W1 bázisává és W2 bázisává: B'UD és DUC'-vel. Feltehető, hogy B' elemei különböznek C' elemeitől, mert ha nem, akkor különbözőkkémeg nyújthatók.
hiszen D elemeit kétszer számoltuk.
