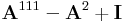Szerkesztő:Mozo/Linalg gyakorló 1.
Mozo (vitalap | szerkesztései) (→Egyenletrendszerek) |
Mozo (vitalap | szerkesztései) (→Egyenletrendszerek) |
||
| 69. sor: | 69. sor: | ||
Megoldások: inhomogén: (-1,0,1). Ker(A)={t(-2,1,1)} | Megoldások: inhomogén: (-1,0,1). Ker(A)={t(-2,1,1)} | ||
| + | |||
| + | ==Sajátértékfeladatok== | ||
| + | '''1.''' Legyen '''A''' az x+y=0 egyenesre tükrötés operátora. Számítsa ki az | ||
| + | :<math>\mathbf{A}^{111}-\mathbf{A}^2+\mathbf{I}\,</math> | ||
| + | leképezés sajátértékeit és sajátvektorait! | ||
A lap 2009. március 12., 19:15-kori változata
Alterek
1. Igazolja, hogy ha W1 és W2 altér V-ben, akkor
 altér
altér
Ugyanis, ha u,v ∈ W1∩W2, akkor u,v ∈W1 és u,v ∈ W2, de ezek zártak az összeadásra és a számmal való szorzásra, ezért: u+v ∈ W1 és u+v ∈ W2,, azaz u+v ∈ W1∩W2 és λ.u ∈ W1 és λ.u ∈ W2, azaz λ.u∈ W1∩W2,.
2. Igazoljuk, hogy ha W1 és W2 altér V-ben és W1∩W2, ≠ {0}, akkor
Először belátjuk, hogy
ha B bázis W1-ben és C bázis W2-ben BUC generátorrendszere 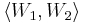 -nek, de nem nagyobb a számossága, mint |B|+|C|
-nek, de nem nagyobb a számossága, mint |B|+|C|
Most belátjuk, a szigorú egyenlőtlenséget. W1∩W2 altér mindkét altérben, ezért ha a metszet nem 0, akkor egy D ⊆ W1∩W2 bázis kiegészíthető W1 bázisává és W2 bázisává: B'UD és DUC'-vel. Feltehető, hogy B' elemei különböznek C' elemeitől, mert ha nem, akkor különbözőkkémeg nyújthatók.
hiszen D elemeit kétszer számoltuk.
Egyenletrendszerek
1.
Ax=b-nek pontosan akkor van megoldása, ha r(A)=r(A|b). r(A) az oszlopok által kifeszített altér dimenziója.
hisz egyrészt csak háromemeletesek, másrészt van három független (1.,2.,4. oszlop). r(A)=3 pontosan akkor, ha a=-1. Ezesetben pedig valóban 1 megoldás van, mert det(A) ≠ 0.
Megoldás: x_0+Ker(A), Ker(A)={0}, mert A invertálható:
x_0=(1,2,1)
2.
Megoldhatóság: b=0
Megoldások száma: végtelen, mert dimKer(A)=3-dimIm(A)=3-2=1
Megoldások: inhomogén: (-1,0,1). Ker(A)={t(-2,1,1)}
Sajátértékfeladatok
1. Legyen A az x+y=0 egyenesre tükrötés operátora. Számítsa ki az
leképezés sajátértékeit és sajátvektorait!
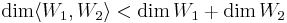
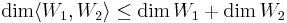
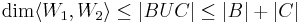
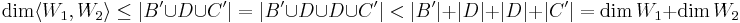
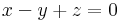
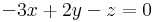
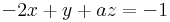
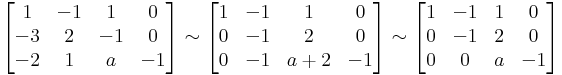
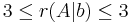
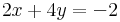
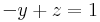
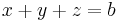
![[\mathbf{A}|\mathbf{y}]\sim\begin{bmatrix}
2 & 4 & 0 & -2\\
0 & -1 & 1 & 1\\
1 & 1 & 1 & b
\end{bmatrix}\sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & -1 & 1 & b+1
\end{bmatrix} \sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & 0 & 0 & b
\end{bmatrix}](/upload/math/2/d/3/2d31510649347ec9a67463a4faf92c74.png)