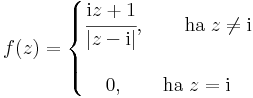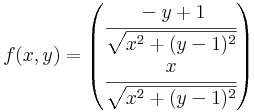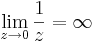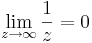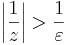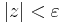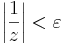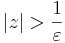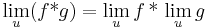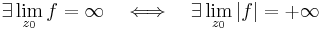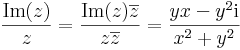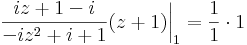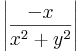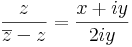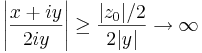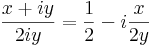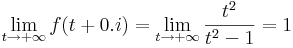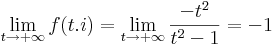Matematika A3a 2008/5. gyakorlat
Feladat folytonosságra
Feladat. Folytonos-e a z = i-ben az
Ha z = x + iy és (x,y) ≠ (0,1), akkor:
Már az első komponens határértéke sem létezik, hisz (x,y)=(0,y) mentén alulról a (0,1)-hez tartva a határérték -1, az x=y-1 mentén pedig -1/gyök kettő.
A második tényező szintén nem.
Határérték
Komplex függvény C-beli pontban vett C-beli határértéke ugyanúgy értelmezett, mint az R2 esetben. Itt is érvényes, hogy pontosan akkor látezik a határérték, ha a komponensfüggvényeknek létezik a határértéke és ekkor a határérték egyenlő lesz a valós és képzetes komponens határértékéből alkotott komplex számmal.
A ∞ miatt érdemes külön is megfogalmazni a határérték definícióját, bár az teljesen analóg a valós esettel. Legyen f egy az A ⊆ C halmazon értelmezett, C-be képező függvény. Legyen 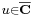 az A torlódási pontja, azaz minden r > 0 esetén legyen olyan a ∈ A, hogy a ∈ Br(u)\{u}. Azt mondjuk, hogy az f-nek a
az A torlódási pontja, azaz minden r > 0 esetén legyen olyan a ∈ A, hogy a ∈ Br(u)\{u}. Azt mondjuk, hogy az f-nek a 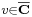 elem határértéke az u-ban, ha
elem határértéke az u-ban, ha
- minden ε > 0 esetén létezik olyan δ > 0, hogy minden z ∈ A ∩ Bδ(u)\{u}-re f(z) ∈ Bε(v)
ahol természetesen a ∞ környezetei a már említett módon értendők.
Feladat. Igazoljuk definíció szerint, hogy
1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| < δ esetén, hogy a függvényérték a ∞ ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
2. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| > 1/δ esetén, hogy a függvényérték a 0-nak ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| > 1/δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
A végtelen határérékkel történő számolás szabályai előtt definiálnunk kell néhány kibővített műveletet. Ezt a következők szellemében tesszük:
- Ha a és b valamelyike a ∞ szimbólum (a másik, ha nem ilyen, akkor komplex szám), akkor az a * b alapműveletet akkor értelmezzük a c szimbólumként (mely szintén vagy komplex szám, vagy az ∞), ha minden a határértékű f függvény esetén és minden b határértékű g függvény esetén a f*g szükségszerűen a c-hez tart. Ekkor mondjuk tehát, hogy az
- a * b = c
- definíció jó.
Például a ∞ + ∞ művelet feltétlenül értelmezett és értéke a ∞, mert könnyen látható, hogy bármely két, a ∞-hez tartó függvény összege is a ∞-hez tart. De a 0  ∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z))
∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z))  Re(z)
Re(z)  1, a z=0-ban, de (1/Re(z))
1, a z=0-ban, de (1/Re(z))  2 Re(z)
2 Re(z)  2 a z=0-ban.
2 a z=0-ban.
Definíció – Végtelen és alapműveletek – Az alábbi műveleti szabályokat vezetjük be a ∞, szimbólumra vonatkozóan, az alábbiakban z tetszőleges komplex szám, n tetszőleges nemnulla komplex szám:
-
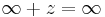 ,
,
-
 ,
,
-
 ,
,
-
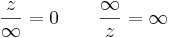 ,
,
továbbá a szorzás és az összeadás kommutatív.
Megjegyezzük még, hogy 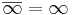 , azaz a végtelen konjugáltja saját maga.
, azaz a végtelen konjugáltja saját maga.
Definíció – Határozatlan esetek – Az alábbi alapműveletek nem értelmezhetők:
-
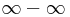 ,
,
-
 ,
,
-
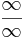 ,
,
-
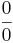
Tétel – Végtelen határérték és alapműveletek – Ha az f és g komplex függvényeknek létezik határértékük az 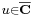 helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:
helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:
Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
A bizonyításról. Ennek a tételnek a bizonyítása minden nehézség nélkül elvégezhető vagy az R2-beli sorozatokra vonatkozó átviteli elv vagy a komponensfüggvények határértékére történő hivatkozás útján. Minenekelőtt azt kell szem előtt tartanunk, hogy a végtelenhez való tartás, a függvény abszolútértékének plusz végtelenhez tartását jelenti:
Feladat. Adjuk példákat arra, hogy a határozatlan alakú határértékeket valóban nem lehet definiálni.
Nézzük a 0-ban az alábbi függvényeket:
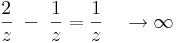 miközben
miközben 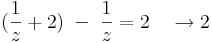
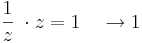 miközben
miközben 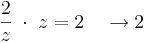
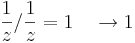 miközben
miközben 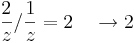
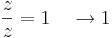 miközben
miközben 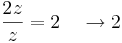
Feladat. Számítsuk ki az alábbi határértékeket, ha léteznek!
-
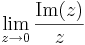 ,
,
-
 ,
,
-
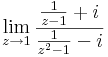 ,
,
-
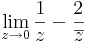 ,
,
-
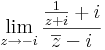 ,
,
Megoldás. 1. nemnulla z-re:
de ekkor például az első komponensfüggvény x = 0 felől közelítve 0, míg az x = y-felől:1/2, azaz nem létezik az első komponensnek a (0,0)-ban határértéke, azaz a komplex függvénynek sem.
2. 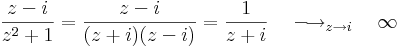
3. 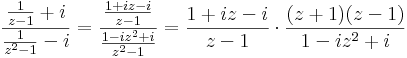
4. 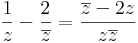 csak a valós részt nézve:
csak a valós részt nézve:
az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs határérték.
5. 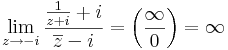 .
.
Feladat. Adjuk meg minden z0 ∈ C számra az alábbi függvény határértékét!
-
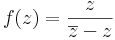 ,
,
-
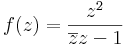 ,
,
1. 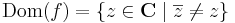
Folytonos az értelmezési tartományában. A határon:
z0 ≠ 0 esetén
z0 = 0 esetén:
ismert, hogy nincs határérték.
2. 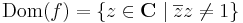
Az egységkör pontjaitól különbözőkre folytonos, az egységkörön a végtelen, a végtelenben pedig nincs határérték. Ugyanis:
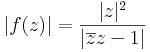 ,
,
így az egységkörön a számláló az 1-hez, a nevező a nullához tart. A végtelenben pedig t valóssal: