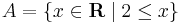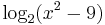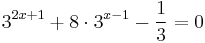Érettségi gyakorló 1.
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Exponenciális egyenlet) |
Mozo (vitalap | szerkesztései) |
||
| 32. sor: | 32. sor: | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
|- bgcolor="#efefef" | |- bgcolor="#efefef" | ||
| − | ||[[Érettségi gyakorló 1./Megoldások|Megoldás]] | + | ||[[Érettségi gyakorló 1./Megoldások#Exponenciális egyenlet|Megoldás]] |
|} | |} | ||
| + | |||
| + | Ha nem ment, akkor egyszerűbb: | ||
| + | |||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | ||[[Érettségi gyakorló 1./Megoldások#Exponenciális egyenlet gyakorló|Gyakorló]] | ||
| + | |} | ||
| + | |||
<center> | <center> | ||
A lap 2017. március 31., 22:07-kori változata
Halmazműveletek
Intervallumos feladat
Legyen
és B a
kifejezés értelmezési tartománya. Adja meg az
- a)
 és
és
- b)
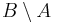
- c)
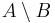
- d)

halmazokat!
| Megoldás |
Ha nem ment, akkor egyszerűbb:
| Gyakorló |
Exponenciális egyenlet
Oldja meg az
egyenletet a valós számok halmazán!
| Megoldás |
Ha nem ment, akkor egyszerűbb:
| Gyakorló |
| Középiskolás főlap | Érettségi gyakorló 2. |