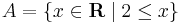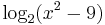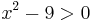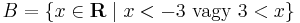Érettségi gyakorló 1./Megoldások
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Intervallumos halmazos) |
Mozo (vitalap | szerkesztései) (→Intervallumos halmazos) |
||
| 15. sor: | 15. sor: | ||
kifejezéssel kapcsolatban tudjuk, logaritmus mellett csak pozitív szám állhat, ezért | kifejezéssel kapcsolatban tudjuk, logaritmus mellett csak pozitív szám állhat, ezért | ||
:<math>x^2-9>0\;</math> | :<math>x^2-9>0\;</math> | ||
| − | <math>x^2-9</math> képe egy fölfelé nyitott parabola, <math>x=\pm 3</math> gyökökkel, ezért ez a kifejezés <math>x | + | <math>x^2-9</math> képe egy fölfelé nyitott parabola, <math>x=\pm 3</math> gyökökkel, ezért ez a kifejezés <math>x<-3</math> ill. <math>3<x</math> esetekben pozitív: |
:<math>B=\{x\in\mathbf{R}\mid x<-3\mbox{ vagy }3<x\} | :<math>B=\{x\in\mathbf{R}\mid x<-3\mbox{ vagy }3<x\} | ||
</math> | </math> | ||
| − | + | **************** ********************> | |
| + | -3 3 | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
|- bgcolor="#efefef" | |- bgcolor="#efefef" | ||
||[[Érettségi gyakorló 1.#Intervallumos feladat|vissza]] | ||[[Érettségi gyakorló 1.#Intervallumos feladat|vissza]] | ||
|} | |} | ||
A lap 2017. március 31., 20:24-kori változata
Intervallumos halmazos
Legyen
és 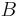 a
a
kifejezés értelmezési tartománya. Adja meg az
- a)
 ,
,
- b)
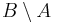 ,
,
- c)
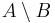 és
és
- d)
 .
.
halmazokat!
MO.: A
kifejezéssel kapcsolatban tudjuk, logaritmus mellett csak pozitív szám állhat, ezért
x2 − 9 képe egy fölfelé nyitott parabola, 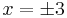 gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
**************** ********************>
-3 3
| vissza |