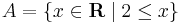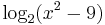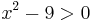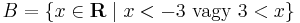Érettségi gyakorló 1./Megoldások
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Intervallumos halmazos) |
Mozo (vitalap | szerkesztései) (→Intervallumos halmazos) |
||
| 18. sor: | 18. sor: | ||
:<math>B=\{x\in\mathbf{R}\mid x<-3\mbox{ vagy }3<x\} | :<math>B=\{x\in\mathbf{R}\mid x<-3\mbox{ vagy }3<x\} | ||
</math> | </math> | ||
| + | Ami kell: | ||
| + | :<math>A\cap B</math> azaz ''A'' és ''B'' közös elemei, | ||
| + | :<math>B\setminus A</math> ''B''-ből kivéve ''A'' elemeit, | ||
| + | :c) <math>A\setminus B</math> ''A''-ból kivéve ''B'' elemeit, | ||
| + | :d) <math>A\cup B</math> azok az elemek, amik ''A'' ill. ''B'' közül legalább az egyikben benne vannak. | ||
| + | halmazokat! | ||
| + | |||
| + | |||
A: ----------------O O-------------------> | A: ----------------O O-------------------> | ||
-3 3 | -3 3 | ||
A lap 2017. március 31., 21:14-kori változata
Intervallumos halmazos
Legyen
és 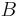 a
a
kifejezés értelmezési tartománya. Adja meg az
- a)
 ,
,
- b)
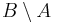 ,
,
- c)
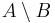 és
és
- d)
 .
.
halmazokat!
MO.: A
kifejezéssel kapcsolatban tudjuk, logaritmus mellett csak pozitív szám állhat, ezért
x2 − 9 képe egy fölfelé nyitott parabola, 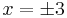 gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
Ami kell:
 azaz A és B közös elemei,
azaz A és B közös elemei,
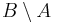 B-ből kivéve A elemeit,
B-ből kivéve A elemeit,
- c)
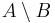 A-ból kivéve B elemeit,
A-ból kivéve B elemeit,
- d)
 azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
halmazokat!
A: ----------------O O------------------->
-3 3
B: *------------------->
2
A∩B: O------------------->
3
B\A: *-*
2 3
A\B: -------------O
-3
A∪B: --------------O *------------------->
-3 2
A grafikonokról a halmazok:
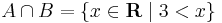 ,
,
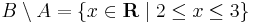 ,
,
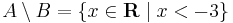 és
és
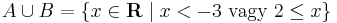 .
.
| vissza |