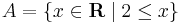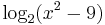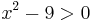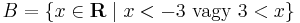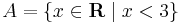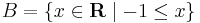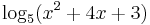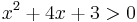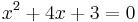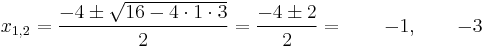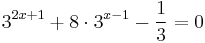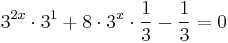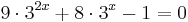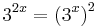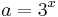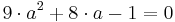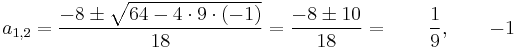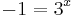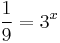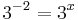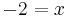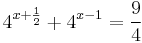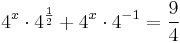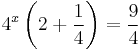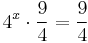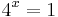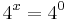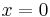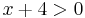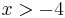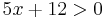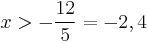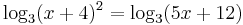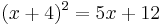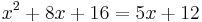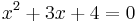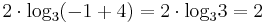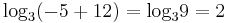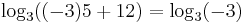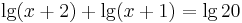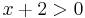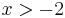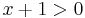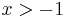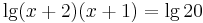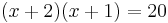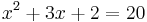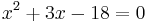Érettségi gyakorló 1./Megoldások
Mozo (vitalap | szerkesztései) (→Logaritmikus egyenlet) |
Mozo (vitalap | szerkesztései) (→Logaritmikus egyenlet) |
||
| 185. sor: | 185. sor: | ||
:<math>2\cdot\mathrm{log}_3(x+4)=\mathrm{log}_3(5x+12)\;</math> | :<math>2\cdot\mathrm{log}_3(x+4)=\mathrm{log}_3(5x+12)\;</math> | ||
a 2-t bevihetjük a logaritmus mellett álló kifejezés kitevőjébe az alábbi azonosság alapján: | a 2-t bevihetjük a logaritmus mellett álló kifejezés kitevőjébe az alábbi azonosság alapján: | ||
| − | :<math>n\cdot \mathrm{log}_a x=\mathrm{log}_a x^n</math> (ahol <math>x>0</math>, <math>a>0</math>, ''a''≠1) | + | :<math>\boxed{n\cdot \mathrm{log}_a x=\mathrm{log}_a x^n}</math> (ahol <math>x>0</math>, <math>a>0</math>, ''a''≠1) |
Tehát: | Tehát: | ||
:<math>\mathrm{log}_3(x+4)^2=\mathrm{log}_3(5x+12)\;</math> | :<math>\mathrm{log}_3(x+4)^2=\mathrm{log}_3(5x+12)\;</math> | ||
A lap 2017. április 1., 07:11-kori változata
Tartalomjegyzék |
Intervallumos halmazos
Legyen
és 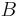 a
a
kifejezés értelmezési tartománya. Adja meg az
- a)
 ,
,
- b)
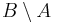 ,
,
- c)
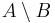 és
és
- d)
 .
.
halmazokat!
MO.: A
kifejezéssel kapcsolatban tudjuk, logaritmus mellett csak pozitív szám állhat, ezért
x2 − 9 képe egy fölfelé nyitott parabola, 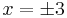 gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
gyökökkel, ezért ez a kifejezés x < − 3 ill. 3 < x esetekben pozitív:
Ami kell:
 azaz A és B közös elemei,
azaz A és B közös elemei,
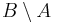 B-ből kivéve A elemeit,
B-ből kivéve A elemeit,
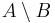 A-ból kivéve B elemeit,
A-ból kivéve B elemeit,
 azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
halmazokat!
A: ----------------O O------------------->
-3 3
B: *------------------->
2
A∩B: O------------------->
3
B\A: *-*
2 3
A\B: -------------O
-3
A∪B: --------------O *------------------->
-3 2
A grafikonokról a halmazok:
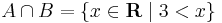 ,
,
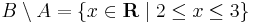 ,
,
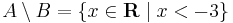 és
és
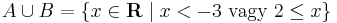 .
.
| vissza |
Intervallumos halmazos gyakorló
Intervallumokkal végzett műveletek
Legyen
és
Adja meg az
- a)
 ,
,
- b)
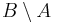 ,
,
- c)
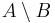 és
és
- d)
 .
.
halmazokat!
MO.: Ami kell:
 azaz A és B közös elemei,
azaz A és B közös elemei,
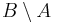 B-ből kivéve A elemeit,
B-ből kivéve A elemeit,
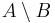 A-ból kivéve B elemeit,
A-ból kivéve B elemeit,
 azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
azok az elemek, amik A ill. B közül legalább az egyikben benne vannak.
halmazokat!
A: ----------------O
3
B: *------------------->
-1
A∩B: *----------O
-1 3
A\B: ------O
-1
B\A: *------------------->
3
A∪B: --------------------------------------->
A grafikonokról a halmazok:
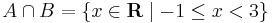 ,
,
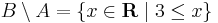 ,
,
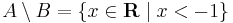 és
és
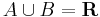 .
.
Logaritmusos függvény értelmezési tartománya
Mi az
kifejezés értelmezési tartománya?
MO.: Logaritmus mellett csak pozitív szám állhat:
ez egy felfelé nyitott parabola és két zérushelye:
Akkor pozitív a függvényérték, ha x < − 3 vagy − 1 < x:
----------------O O-------------------->
-3 -1
| vissza |
Exponenciális egyenlet
Oldja meg az
egyenletet a valós számok halmazán!
MO.: Ha a kitevőben összeg van, akkor érdemes a hatványok közötti szorzatot felírni:
3-mal beszorozva, hogy ne kelljen törtekkel számolni:
Itt felismerhetjünk, hogy
Bevezetve az
új ismeretlent:
Innen az új ismeretlent definiáló egynletbe visszahelyettesítve, egyfelől:
ami lehetetlen, továbbá:
exp. sz. m.
Exponenciális egyenlet gyakorló
Oldja meg az
egyenletet a valós számok halmazán!
MO.: Ha a kitevőben összeg van, akkor érdemes a hatványok közötti szorzatot felírni:
mivel 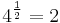 ezért kiemelve 4x-t
ezért kiemelve 4x-t
azaz
azaz
bármely szám nulladik hatvány 1,
exp. sz. m.
| vissza |
Logaritmikus egyenlet
Oldja meg a
egyenletet a valós számok halmazán!
MO.: Kikötések:
azaz
és
azaz
Számegyenesen ábrázolva:
O---------------------------------------->
-4
O-------------------------->
-2,4
A közös rész:
O-------------------------->
-2,4
azaz
a 2-t bevihetjük a logaritmus mellett álló kifejezés kitevőjébe az alábbi azonosság alapján:
- Értelmezés sikertelen (ismeretlen függvény\boxed): \boxed{n\cdot \mathrm{log}_a x=\mathrm{log}_a x^n}
(ahol x > 0, a > 0, a≠1)
Tehát:
hivatkozva szigorú monotonitásra, elhagyható a logaritmus:
aminek a gyökei a másodfokú egyenlet megoldóképlete alapján:
- -3 és -1
A -1 megoldás, mert behelyettesítve az eredeti egyenletbe:
De a -3 nem megoldás, mert ekkor a jobb oldal nincs értelmezve
| vissza |
Logaritmikus egyenlet gyakorló
Oldja meg az
egyenletet a valós számok halmazán!
MO.: Kikötések:
azaz
és
azaz
Számegyenesen ábrázolva:
O---------------------------------------->
-2
O-------------------------->
-1
A közös rész:
O-------------------------->
-1
azaz
a két tízes alapú logaritmust egyesíthetjük az alábbi azonosság alapján:
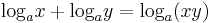 (ahol x,y > 0, a > 0, a≠1)
(ahol x,y > 0, a > 0, a≠1)
tehát:
hivatkozva a szigorú monotonitásra, elhagyható a logaritmus:
aminek a gyökei a másodfokú egyenlet megoldóképlete alapján:
- -6 és 3
amelyek közül a -6 nem felel meg az x > − 1 kikötésnek, de a 3 megoldás, mert:
| vissza |