7. házi feladat
| 1. sor: | 1. sor: | ||
| − | LKR megszerkesztése: | + | * LKR megszerkesztése: |
Az előadáson bemutatott lkr.py módosítása úgy, hogy az LKR hossza mellett határozzunk meg egy konkrét | Az előadáson bemutatott lkr.py módosítása úgy, hogy az LKR hossza mellett határozzunk meg egy konkrét | ||
| 5. sor: | 5. sor: | ||
feljegyezzük egy kétdimenziós tömbben, hogy a legjobb értéket honnan kaptuk. Miután c-t kitöltöttük, visszafelőlről | feljegyezzük egy kétdimenziós tömbben, hogy a legjobb értéket honnan kaptuk. Miután c-t kitöltöttük, visszafelőlről | ||
meghatározható egy LKR. | meghatározható egy LKR. | ||
| + | |||
| + | * Backtrack alkalmazása pénzváltásra: | ||
| + | |||
| + | A 8 vezér probléma megoldása alapján alkalmazzuk a backtrack algoritmust a pénzváltás problémára. | ||
| + | A probléma a következő: | ||
| + | |||
| + | Adott S pénzösszeg és P = {<math>p_1, ... , p_n</math>} pozitív egészek esetén keresem az összes olyan | ||
| + | S = {<math>s_1, ..., s_n </math>} nemnegatív szám n-est, melyre <math>\sum_{x=1}^{n} p_i*s_i</math> egyenlő S-sel. | ||
| + | A megoldás osztály a BackTrack-ből legyen leszármaztatva, és írjuk meg az ősosztály virtuális (pass-szal definiált) tagfüggvényeit. | ||
| + | |||
| + | Példa használatra:<br> | ||
| + | (amikor még 72 Ft volt egy kőrözöttes szendvics)<br><br> | ||
| + | |||
| + | c = Change([1,2,5,10], 72)<br> | ||
| + | c.main()<br><br> | ||
| + | |||
| + | Kimenet: | ||
| + | *[http://info.ilab.sztaki.hu/~kisstom/info2_2011/7het/hazi/out change_out] | ||
A lap 2011. március 23., 12:50-kori változata
- LKR megszerkesztése:
Az előadáson bemutatott lkr.py módosítása úgy, hogy az LKR hossza mellett határozzunk meg egy konkrét közös részsorozatot, melynek hossza maximális. Ez történhet például úgy, hogy a c[i][j] értékek meghatározásakor feljegyezzük egy kétdimenziós tömbben, hogy a legjobb értéket honnan kaptuk. Miután c-t kitöltöttük, visszafelőlről meghatározható egy LKR.
- Backtrack alkalmazása pénzváltásra:
A 8 vezér probléma megoldása alapján alkalmazzuk a backtrack algoritmust a pénzváltás problémára. A probléma a következő:
Adott S pénzösszeg és P = {p1,...,pn} pozitív egészek esetén keresem az összes olyan
S = {s1,...,sn} nemnegatív szám n-est, melyre 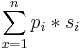 egyenlő S-sel.
A megoldás osztály a BackTrack-ből legyen leszármaztatva, és írjuk meg az ősosztály virtuális (pass-szal definiált) tagfüggvényeit.
egyenlő S-sel.
A megoldás osztály a BackTrack-ből legyen leszármaztatva, és írjuk meg az ősosztály virtuális (pass-szal definiált) tagfüggvényeit.
Példa használatra:
(amikor még 72 Ft volt egy kőrözöttes szendvics)
c = Change([1,2,5,10], 72)
c.main()
Kimenet: