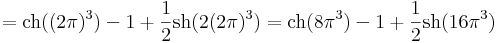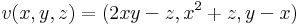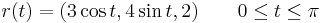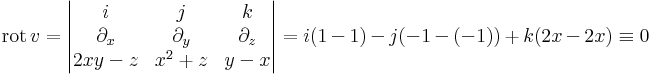A3 2009 gyak 1
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 17. sor: | 17. sor: | ||
:<math>+[t\cos t-\sin t]_0^{2\pi} +\frac{1}{6}[\sin^6t]_0^{2\pi}+[-t^2\sin t+2t\cos t-2\sin t]_0^{2\pi}=</math> | :<math>+[t\cos t-\sin t]_0^{2\pi} +\frac{1}{6}[\sin^6t]_0^{2\pi}+[-t^2\sin t+2t\cos t-2\sin t]_0^{2\pi}=</math> | ||
:<math>=\mathrm{ch}((2\pi)^3)-1+\frac{1}{2}\mathrm{sh}(2(2\pi)^3)=\mathrm{ch}(8\pi^3)-1+\frac{1}{2}\mathrm{sh}(16\pi^3)</math> | :<math>=\mathrm{ch}((2\pi)^3)-1+\frac{1}{2}\mathrm{sh}(2(2\pi)^3)=\mathrm{ch}(8\pi^3)-1+\frac{1}{2}\mathrm{sh}(16\pi^3)</math> | ||
| + | |||
| + | '''2.''' Integráljuk a | ||
| + | :<math>v(x,y,z)=(2xy-z,x^2+z,y-x)\,</math> | ||
| + | vektormezőt az | ||
| + | :<math>r(t)=(3\cos t,4\sin t,2)\quad\quad 0\leq t\leq \pi</math> | ||
| + | görbe mentén! | ||
| + | |||
| + | ''Mo.'' A vektormező rotációmentes: | ||
| + | :<math>\mathrm{rot}\, v=\begin{vmatrix}i & j & k\\ \partial_x & \partial_y &\partial_z \\ 2xy-z & x^2+z & y-x\end{vmatrix}=i(1-1)-j(-1-(-1))+k(2x-2x)\equiv 0</math> | ||
A lap 2009. október 27., 10:45-kori változata
1. Integrálja a
vektormezőt az
görbe mentén!
Mo.
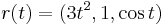
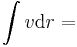
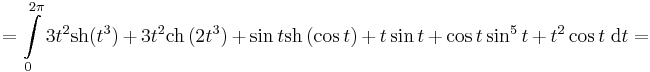
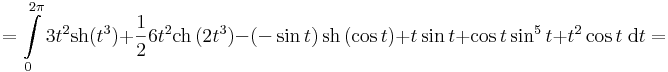
- itt
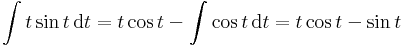
- és
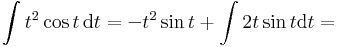
- itt
ezért
2. Integráljuk a
vektormezőt az
görbe mentén!
Mo. A vektormező rotációmentes:
![v(x,y,z)=(\mathrm{sh}(y^2\sqrt[3]{x})+\mathrm{ch}\,(x+y^3),z\,\mathrm{sh}\,(\cos y)+yz,z^5+y^2)](/upload/math/5/5/3/553ca9b8ca0bf5a814d1ada9892b7d07.png)
![r(t)=(t^3,t,\sin t),\quad\quad t\in[0,2\pi]](/upload/math/b/4/4/b44634145192b4ccc45c6423bf4a50ef.png)
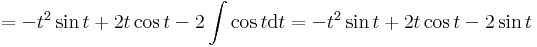
![=[\mathrm{ch}(t^3)]_0^{2\pi}+\frac{1}{2}[\mathrm{sh}\,(2t^3)]_0^{2\pi}-[\mathrm{ch}\,(\cos t)]_0^{2\pi}+](/upload/math/0/7/c/07cbc6914921034b3f7614bf4856fd22.png)
![+[t\cos t-\sin t]_0^{2\pi} +\frac{1}{6}[\sin^6t]_0^{2\pi}+[-t^2\sin t+2t\cos t-2\sin t]_0^{2\pi}=](/upload/math/1/c/1/1c17addd60523ef0c553f8578b9951b0.png)