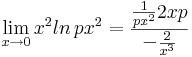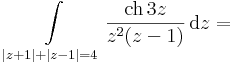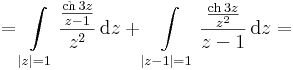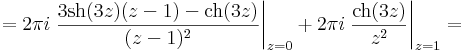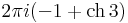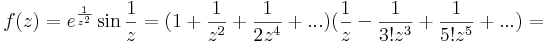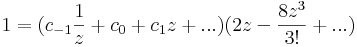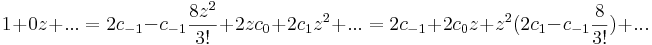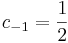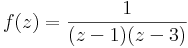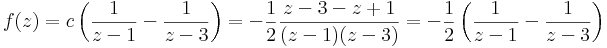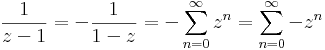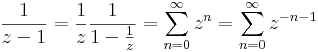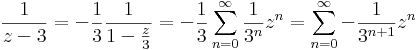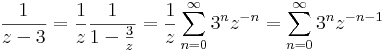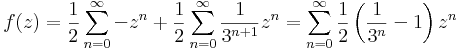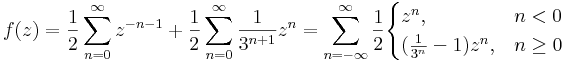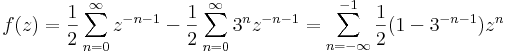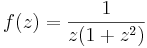A3 2009 gyak 2
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Homogén fokszámú egyenlet) |
||
| (egy szerkesztő 11 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
==Szeparábilis differenciálegyenlet== | ==Szeparábilis differenciálegyenlet== | ||
'''1.''' Oldjuk meg az | '''1.''' Oldjuk meg az | ||
| − | :<math>y'=x | + | :<math>y'=\sin(x)y\,\mathrm{ln}\,y</math> |
egyenletet az | egyenletet az | ||
| − | :a) <math> y(0)= | + | :a) <math> y(0)=1\,</math> |
| − | :b) <math>y(0)=\ | + | :b) <math>y(0)=e\,</math> |
| − | + | kezdeti feltételek mellett! | |
| − | ''Mo.'' a) | + | ''Mo.'' a) Az egyenlet konstans megoládsa az y(x)=1. Ez a kezdeti feltételnek megfelel. |
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást: | b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást: | ||
| − | :<math>\frac{ | + | :<math>\frac{1}{y\,\mathrm{ln}\,y}y'=\sin x </math> |
| − | :<math> | + | :<math>\frac{1}{y}\mathrm{ln}^{-1}(y)y'=\sin x</math> |
| − | :<math>\ | + | :<math>\mathrm{ln}\,|\mathrm{ln}\,y|=-\cos x+C</math> |
| − | + | ez az implicit egyenlet. Ha x=0 és y=e, akkor | |
| − | :<math> | + | :<math>0=-1+C\,</math>, <math>C=1\,</math> |
| − | + | ||
| − | + | ||
és | és | ||
| − | :<math>y(x)= | + | :<math>y(x)=e^{e^{(1-\cos x)}}</math> |
| − | + | ||
| + | ''Megjegyzés.'' Minden '''R'''× '''R'''<sup>+</sup>-beli kezdeti feltételre egyértelműen létezik a megoldás. | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Homogén fokszámú egyenlet== | ==Homogén fokszámú egyenlet== | ||
Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha | Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha | ||
| 30. sor: | 25. sor: | ||
A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az | A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az | ||
:<math>u=\frac{y}{x}\,</math> | :<math>u=\frac{y}{x}\,</math> | ||
| − | új változó bevezetésével, ahol ''u'' = ''u''(''x'') az ismeretlen függvény. Ekkor | + | új változó bevezetésével, ahol ''u'' = ''u''(''x'') az ismeretlen függvény. Tehát: |
| + | :<math>y=ux\,</math> | ||
| + | Ekkor | ||
:<math>(xu)'=u+xu'=y'\,</math> | :<math>(xu)'=u+xu'=y'\,</math> | ||
azaz | azaz | ||
:<math>y'=u'x+u\,</math> | :<math>y'=u'x+u\,</math> | ||
| − | '''2.''' Oldjuk meg az | + | '''2.''' Oldjuk meg az |
| − | :<math>y'xy=x^ | + | :<math>y'xy^3=x^4+y^4\,</math> |
egyenletet! | egyenletet! | ||
| + | ''Mo.'' Általános megoldás: | ||
| + | :<math>(u'x+u)xu^3x^3=x^4+u^4x^4\,</math> | ||
| + | :<math>u'xu^3+u^4=1+u^4\,</math> | ||
| + | :<math>u'u^3x=1\,</math> | ||
| + | :<math>u'u^3=\frac{1}{x}\,</math> | ||
| + | :<math>\frac{u^4}{4}=\mathrm{ln}\,|x|+C\,</math> | ||
| + | :<math>u=\pm\sqrt[4]{4\mathrm{ln}\,|x|+4C}\,</math> | ||
| + | :<math>y=\pm x\sqrt[4]{\mathrm{ln}\,px^4}\,</math> | ||
| − | + | A szinguláris megoldás: ha <math>x_0=0</math>, akkor y szükségképpen 0. Itt viszont nem reguláris a differenciálegyenlet: | |
| − | :<math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | :<math>\lim\limits_{x\to 0}x^2ln\,px^2=\frac{\frac{1}{px^2}2xp}{-\frac{2}{x^3}}</math> | |
| − | :<math> | + | azaz a 0-hoz tart, így legalább kettő (valójában végtelen) megoldás halad át a (0,0) ponton. |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Cauchy-típusú integrálok== | ==Cauchy-típusú integrálok== | ||
'''3.''' | '''3.''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:a) <math>\int\limits_{|z+1|+|z-1|=4}\frac{\mathrm{ch}\,3z}{z^3-z^2}\,\mathrm{d}z</math> | :a) <math>\int\limits_{|z+1|+|z-1|=4}\frac{\mathrm{ch}\,3z}{z^3-z^2}\,\mathrm{d}z</math> | ||
:(a görbe egy pozitívan irányított 0 középponttú ellipszis) és a | :(a görbe egy pozitívan irányított 0 középponttú ellipszis) és a | ||
| 93. sor: | 58. sor: | ||
:d) Adja meg a reziduumokat a z=0-ban! | :d) Adja meg a reziduumokat a z=0-ban! | ||
| − | + | ''Mo.'' a) | |
| − | '' | + | :<math>\int\limits_{|z+1|+|z-1|=4}\frac{\mathrm{ch}\,3z}{z^2(z-1)}\,\mathrm{d}z=</math> |
| − | : | + | :<math>=\int\limits_{|z|=1}\frac{\frac{\mathrm{ch}\,3z}{z-1}}{z^2}\,\mathrm{d}z+\int\limits_{|z-1|=1}\frac{\frac{\mathrm{ch}\,3z}{z^2}}{z-1}\,\mathrm{d}z=</math> |
| − | : | + | :<math>=2\pi i\left.\frac{3\mathrm{sh}(3z)(z-1)-\mathrm{ch}(3z)}{(z-1)^2}\right|_{z=0}+2\pi i\left.\frac{\mathrm{ch}(3z)}{z^2}\right|_{z=1}=</math> |
| − | : | + | :<math>2\pi i(-1+\mathrm{ch}\,3)\,</math> |
| + | az első másodfokú pólus, a második tagban egy elsőfokú pólust fedezhtünk föl. A reziduumok az integrálok a 2 pi i-k nélkül. | ||
| − | + | b) A nullabeli 99. deriváltra van szükségünk: | |
| + | :<math>(1-e^{2z})'=-2e^{2z}\,</math>, <math>n=1</math> | ||
| + | :<math>(-2e^{2z})'=-2^2e^{2z}\,</math>, <math>n=2</math> | ||
| − | + | :<math>(-2e^{2z})'=-2^{99}e^{2z}\,</math>, <math>n=99</math> | |
| − | :<math> | + | |
| − | + | ||
| − | </math> | + | |
| − | + | ||
| − | + | <math>\int\limits_{|z|=1}\frac{1-e^{2z}}{z^{100}}\,\mathrm{d}z=\frac{2\pi i}{99!}(-2^{99})</math> | |
| − | + | Ez egy 99-edfokú pólus, residuuma a 2pi i nélküli tényező. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | ==Reziduumszámítás== |
| + | '''4.''' Számítsuk ki az alábbi függvények 0-beli reziduumát, egységkörön vett integrálját és a szakadás jellegét! | ||
:a) <math>f(z)=e^{\frac{1}{z^2}}\sin \frac{1}{z}</math> | :a) <math>f(z)=e^{\frac{1}{z^2}}\sin \frac{1}{z}</math> | ||
:b) <math>g(z)=\frac{\cos z}{\sin ^2 z}</math> | :b) <math>g(z)=\frac{\cos z}{\sin ^2 z}</math> | ||
:c) <math>h(z)=\frac{e^z-1}{\sin z}</math> | :c) <math>h(z)=\frac{e^z-1}{\sin z}</math> | ||
:d) <math>r(z)=\frac{1}{\sin 2z}</math> | :d) <math>r(z)=\frac{1}{\sin 2z}</math> | ||
| − | + | ||
| + | ''Mo.''a) | ||
| + | :<math>f(z)=e^{\frac{1}{z^2}}\sin \frac{1}{z}=(1+\frac{1}{z^2}+\frac{1}{2z^4}+...)(\frac{1}{z}-\frac{1}{3!z^3}+\frac{1}{5!z^5}+...)=</math> | ||
| + | |||
| + | Tehát Res=1 | ||
| + | |||
| + | Lényeges szakadás. | ||
| + | |||
| + | c) Megszüntethető szakadású. Reguláris, res = 0 | ||
| + | |||
| + | d) másodfokú pólus. | ||
| + | :<math> | ||
| + | 1=(c_{-1}\frac{1}{z}+c_0+c_1z+...)(2z-\frac{8z^3}{3!}+...)</math> | ||
| + | :<math>1+0z+...=2c_{-1}-c_{-1}\frac{8z^2}{3!}+2zc_0+2c_1z^2+...=2c_{-1}+2c_0z+z^2(2c_1-c_{-1}\frac{8}{3!})+...</math> | ||
| + | :<math>c_{-1}=\frac{1}{2}</math> | ||
==Laurent-sorfejtés== | ==Laurent-sorfejtés== | ||
A lap jelenlegi, 2009. november 19., 21:31-kori változata
Tartalomjegyzék |
Szeparábilis differenciálegyenlet
1. Oldjuk meg az
egyenletet az
- a)
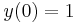
- b)
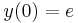
kezdeti feltételek mellett!
Mo. a) Az egyenlet konstans megoládsa az y(x)=1. Ez a kezdeti feltételnek megfelel.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
ez az implicit egyenlet. Ha x=0 és y=e, akkor
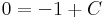 ,
, 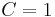
és
Megjegyzés. Minden R× R+-beli kezdeti feltételre egyértelműen létezik a megoldás.
Homogén fokszámú egyenlet
Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha
A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az
új változó bevezetésével, ahol u = u(x) az ismeretlen függvény. Tehát:
Ekkor
azaz
2. Oldjuk meg az
egyenletet! Mo. Általános megoldás:
A szinguláris megoldás: ha x0 = 0, akkor y szükségképpen 0. Itt viszont nem reguláris a differenciálegyenlet:
azaz a 0-hoz tart, így legalább kettő (valójában végtelen) megoldás halad át a (0,0) ponton.
Cauchy-típusú integrálok
3.
- a)
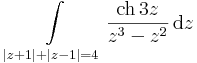
- (a görbe egy pozitívan irányított 0 középponttú ellipszis) és a
- b)
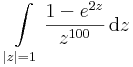
integrálokat!
- c) Milyen szakadások vannak z=0-ban?
- d) Adja meg a reziduumokat a z=0-ban!
Mo. a)
az első másodfokú pólus, a második tagban egy elsőfokú pólust fedezhtünk föl. A reziduumok az integrálok a 2 pi i-k nélkül.
b) A nullabeli 99. deriváltra van szükségünk:
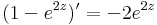 , n = 1
, n = 1
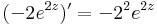 , n = 2
, n = 2
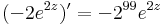 , n = 99
, n = 99
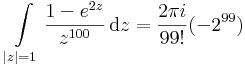 Ez egy 99-edfokú pólus, residuuma a 2pi i nélküli tényező.
Ez egy 99-edfokú pólus, residuuma a 2pi i nélküli tényező.
Reziduumszámítás
4. Számítsuk ki az alábbi függvények 0-beli reziduumát, egységkörön vett integrálját és a szakadás jellegét!
- a)
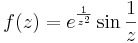
- b)
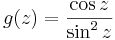
- c)
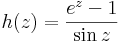
- d)
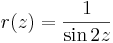
Mo.a)
Tehát Res=1
Lényeges szakadás.
c) Megszüntethető szakadású. Reguláris, res = 0
d) másodfokú pólus.
Laurent-sorfejtés
5. Határozzuk meg az
nulla körüli Laurent-sorait!
Mo.
alkalmas tehát a c=-1/2.
Ha |z|<1, akkor
Ha |z|>1, akkor
A másik tag:
Ha |z/3|<1, azaz |z|<3
Ha |z|>3 , akkor
Tehát a Laurent-sorok:
|z|<1 esetén reguláris:
1<|z|<3 esetén vegyes:
|z|>3 esetén csak főrész:
HF Fejtsük sorba a 0 körül az
függvényt!
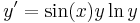
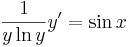
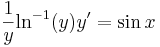
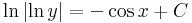
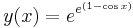
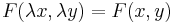
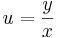
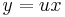
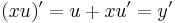
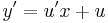
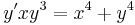
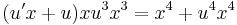
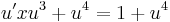
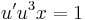
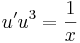
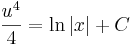
![u=\pm\sqrt[4]{4\mathrm{ln}\,|x|+4C}\,](/upload/math/9/2/c/92c828e446155e1571510d03bc9aa230.png)
![y=\pm x\sqrt[4]{\mathrm{ln}\,px^4}\,](/upload/math/c/5/2/c52a3cc885656d8c54e3886552790237.png)