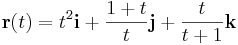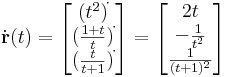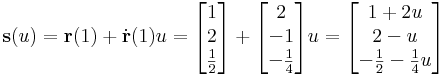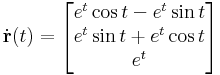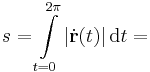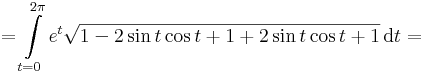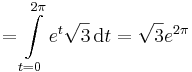A3 2009 vizsga 1
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2009. december 14., 20:51-kor történt szerkesztése után volt.
Differenciálgeometria
1. a) Határozza meg az
görbe azon pontjabeli érintőegyenesének egyenletrendszerét, mely a t=1 értékhez tartozik!
Mo. Az érintőegyenes irányvektora az r függvény t=1-beli deriváltvektora:
Az érintő egyenes vektoregyenlete
1. b) Határozzuk meg a
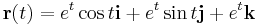 ,
, ![t\in[0,2]](/upload/math/9/f/1/9f15c2e21f34e562b5319f790363a5cd.png)
györbeszakasz ívhosszát!
Mo.