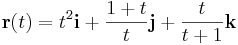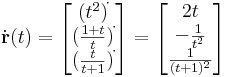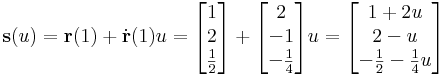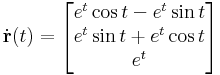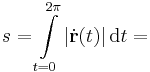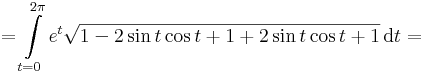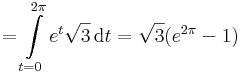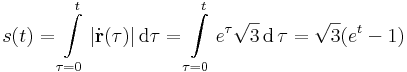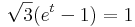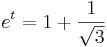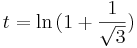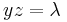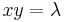A3 2009 vizsga 1
Differenciálgeometria
1. a) Határozza meg az
görbe azon pontjabeli érintőegyenesének egyenletrendszerét, mely a t=1 értékhez tartozik!
Mo. Az érintőegyenes irányvektora az r függvény t=1-beli deriváltvektora:
Az érintő egyenes vektoregyenlete
1. b) Határozzuk meg a
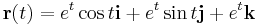 ,
, ![t\in[0,2]](/upload/math/9/f/1/9f15c2e21f34e562b5319f790363a5cd.png)
györbeszakasz ívhosszát! Mennyi t, ha a [0,t] intervallumon a görbe ívhossza 1 egység?
Mo.
A második kérdésre a választ az ívhossz paraméteres felításával tudhatjuk meg. Az integrálási változó legyen egy t-től különböző betű, mondjuk τ vagy t' vagy u. Ekkor
Innen t:
1. c) Mely pontokban párhuzamos az xyz=1 egyenletű felület érintősíkja az x+y+z=5 síkkal?
Mo. 1. mo) Legyen F(x,y,z)=xyz-1. Ekkor a felület egyenlete: F(x,y,z)=0. A felület normálvektorai: grad F = (yz,xz,xy). Kell, hogy grad F párhuzamos legyen az (1,1,1) vektorral, azaz létezzen λ, hogy grad F=λ(1,1,1), azaz
Ekkor x=y=z és λ=+1,-1. Tehát az F=0-t, azaz z=1/xy-t kielégítő megoldások (1,1,1), (-1,-1,1).