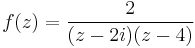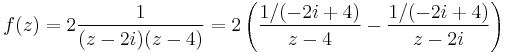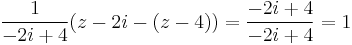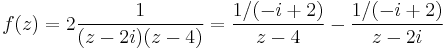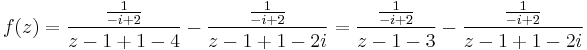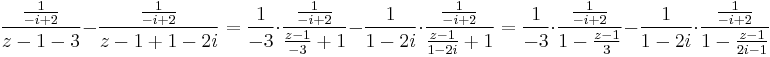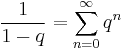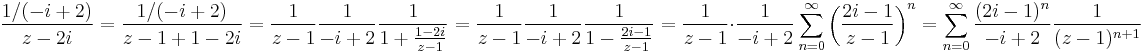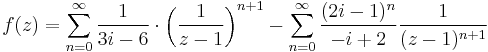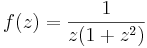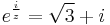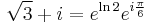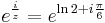A3 2016 gyak 2

A MathWikiből
(Változatok közti eltérés)
(→Laurent-sorfejtés)
36. sor: 36. sor:
 
'''2. a) ''' Oldjuk meg az  
 
'''2. a) ''' Oldjuk meg az  
 
:<math>e^{\frac{i}{z}}=\sqrt{3}+i</math>  
 
:<math>e^{\frac{i}{z}}=\sqrt{3}+i</math>  
−
Egyenletet!
+
egyenletet!
  
−
''Mo.''
+
''Mo.''  
 +
:<math>\sqrt{3}+i=e^{\ln 2}e^{i\frac{\pi}{6}}</math>
 +
mert a szöge 30 fok, a hossza 2. Ezért az egyenlet:
 +
:<math>e^{\frac{i}{z}}=e^{\ln 2 +i\frac{\pi}{6}}</math>
 +
azaz
 +
:<math>\frac{i}{z}=\ln 2 +i\frac{\pi}{6}+2\pi i k</math>
 +
:<math>z=\frac{\frac{\ln 2}{i} +\frac{\pi}{6}+2\pi i k}</math>

A lap 2016. május 2., 15:27-kori változata

Laurent-sorfejtés

1. Határozzuk meg az

f(z)=\frac{2}{(z-2i)(z-4)}

függvény 1 körüli Laurent-sorait!

Mo. Mivel z-2i-(z-4)=-2i+4, ezért

f(z)=2\frac{1}{(z-2i)(z-4)}=2\left(\frac{1/(-2i+4)}{z-4}-\frac{1/(-2i+4)}{z-2i}\right)

és valóban, mert

\frac{1}{-2i+4}(z-2i-(z-4))=\frac{-2i+4}{-2i+4}=1

azaz

f(z)=2\frac{1}{(z-2i)(z-4)}=\frac{1/(-i+2)}{z-4}-\frac{1/(-i+2)}{z-2i}

A sort a z0 = 1 körül kell sorba fejteni, azaz a z − 1 hatványai szerepelnek majd az összegben. Ehhez z-1-nek szerepelnie kell a nevezőkben:

f(z)=\frac{\frac{1}{-i+2}}{z-1+1-4}-\frac{\frac{1}{-i+2}}{z-1+1-2i}=\frac{\frac{1}{-i+2}}{z-1-3}-\frac{\frac{1}{-i+2}}{z-1+1-2i}

Két szingularitás: z = 4 és z = 2i. Ezeknek a távolsága a középponttól:</math> |1-4|=3 és 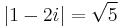|1-2i|=\sqrt{5}. Tehát három lehetőségünk van:

I. A 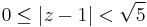0\leq|z-1|<\sqrt{5} körlap,

melyen belül a sor reguláris és z − 1-nek csak nemnegatív hatványai szerepelnek a sorban. Ilyenkor "z − 1 melletti tagból csinálunk mértani sort":

\frac{\frac{1}{-i+2}}{z-1-3}-\frac{\frac{1}{-i+2}}{z-1+1-2i}=\frac{1}{-3}\cdot\frac{\frac{1}{-i+2}}{\frac{z-1}{-3}+1}-\frac{1}{1-2i}\cdot\frac{\frac{1}{-i+2}}{\frac{z-1}{1-2i}+1}=\frac{1}{-3}\cdot\frac{\frac{1}{-i+2}}{1-\frac{z-1}{3}}-\frac{1}{1-2i}\cdot\frac{\frac{1}{-i+2}}{1-\frac{z-1}{2i-1}}

Alkalmazva a

\frac{1}{1-q}=\sum\limits_{n=0}^\infty q^n

formulát, ha | q | < 1 a

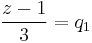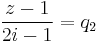
\frac{z-1}{3}=q_1 és \frac{z-1}{2i-1}=q_2

hányadosokra kapjuk:

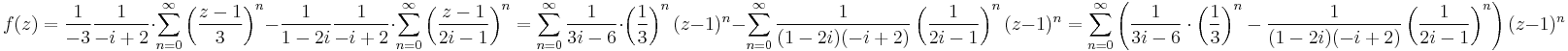
f(z)=\frac{1}{-3}\frac{1}{-i+2}\cdot\sum\limits_{n=0}^\infty\left(\frac{z-1}{3}\right)^n-\frac{1}{1-2i}\frac{1}{-i+2}\cdot\sum\limits_{n=0}^\infty\left(\frac{z-1}{2i-1}\right)^n=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n(z-1)^n-\sum\limits_{n=0}^\infty\frac{1}{(1-2i)(-i+2)}\left(\frac{1}{2i-1}\right)^n(z-1)^n=\sum\limits_{n=0}^\infty\left(\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n-\frac{1}{(1-2i)(-i+2)}\left(\frac{1}{2i-1}\right)^n\right)(z-1)^n
II. A 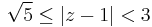\sqrt{5}\leq|z-1|<3 körgyűrű,

melyben az első tag reguláris, de a második már nem. Ilyenkor "a z-1-et emeljük ki a nevezőből":

\frac{1/(-i+2)}{z-2i}=\frac{1/(-i+2)}{z-1+1-2i}=\frac{1}{z-1}\frac{1}{-i+2}\frac{1}{1+\frac{1-2i}{z-1}}=\frac{1}{z-1}\frac{1}{-i+2}\frac{1}{1-\frac{2i-1}{z-1}}=\frac{1}{z-1}\cdot\frac{1}{-i+2}\sum\limits_{n=0}^{\infty}\left(\frac{2i-1}{z-1}\right)^n=\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}}

Tehát itt:

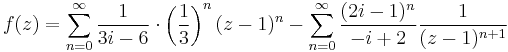
f(z)=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n(z-1)^n-\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}}
Végül a |z-1|>3 körgyűrűn
f(z)=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{z-1}\right)^{n+1}-\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}} 
HF Fejtsük sorba a 0 körül az
f(z)=\frac{1}{z(1+z^2)}\,

függvényt!

Egyenlet megoldás

2. a) Oldjuk meg az

e^{\frac{i}{z}}=\sqrt{3}+i

egyenletet!

Mo.

\sqrt{3}+i=e^{\ln 2}e^{i\frac{\pi}{6}}

mert a szöge 30 fok, a hossza 2. Ezért az egyenlet:

e^{\frac{i}{z}}=e^{\ln 2 +i\frac{\pi}{6}}

azaz

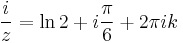
\frac{i}{z}=\ln 2 +i\frac{\pi}{6}+2\pi i k
Értelmezés sikertelen (formai hiba): z=\frac{\frac{\ln 2}{i} +\frac{\pi}{6}+2\pi i k}
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=A3_2016_gyak_2&oldid=11608”
Személyes eszközök