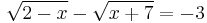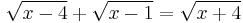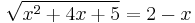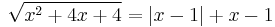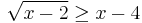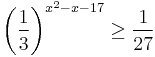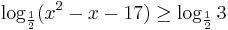Egyenletek
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Gyökös egyenletek és egyenlőtlenségek) |
Mozo (vitalap | szerkesztései) (→Gyökös egyenletek és egyenlőtlenségek) |
||
| 1. sor: | 1. sor: | ||
| − | ==Gyökös egyenletek és egyenlőtlenségek== | + | 2==Gyökös egyenletek és egyenlőtlenségek== |
'''1.''' | '''1.''' | ||
:<math>\sqrt{2-x}-\sqrt{x+7}=-3</math> | :<math>\sqrt{2-x}-\sqrt{x+7}=-3</math> | ||
| 10. sor: | 10. sor: | ||
'''5.''' | '''5.''' | ||
:<math>\sqrt{x-2}\geq x-4</math> | :<math>\sqrt{x-2}\geq x-4</math> | ||
| + | |||
| + | ==Exponenciális és logaritmikus egyenletek és egyenlőtlenségek== | ||
| + | |||
| + | '''6.''' | ||
| + | :<math>\left(\dfrac{1}{3}\right)^{x^2-x-17}\geq \dfrac{1}{27}</math> | ||
| + | |||
| + | '''7.''' | ||
| + | :<math>\log_{\frac{1}{2}}(x^2-x-17)\geq \log_{\frac{1}{2}}3</math> | ||
A lap 2020. október 27., 16:41-kori változata
2==Gyökös egyenletek és egyenlőtlenségek== 1.
2.
3.
4.
5.
Exponenciális és logaritmikus egyenletek és egyenlőtlenségek
6.
7.