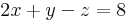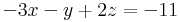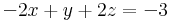Gauss-elimináció
| 1. sor: | 1. sor: | ||
A '''Gauss-elimináció''' egy eljárás, amivel megtalálhatjuk egy lineáris egyenletrendszer megoldásait, meghatározhatjuk egy mátrix rangját. | A '''Gauss-elimináció''' egy eljárás, amivel megtalálhatjuk egy lineáris egyenletrendszer megoldásait, meghatározhatjuk egy mátrix rangját. | ||
| − | Az eljárás során először a kibővített együtthatómátrixot elemi sorekvivalens átalakítások felhasználásával lépcsős alakúra hozzuk, majd a második lépésben redukált | + | Az eljárás során először a kibővített együtthatómátrixot elemi sorekvivalens átalakítások felhasználásával lépcsős alakúra hozzuk, majd a második lépésben redukált lépcsős alakra redukáljuk. |
==Az eljárás leírása== | ==Az eljárás leírása== | ||
| 13. sor: | 13. sor: | ||
* Egy sor konstansszorosának másikhoz való elemenkénti hozzáadása | * Egy sor konstansszorosának másikhoz való elemenkénti hozzáadása | ||
==Példa== | ==Példa== | ||
| + | Oldjuk meg az alábbi lineáris egyenletrendszert: | ||
| + | :<math>2x+y-z=8 \ </math> | ||
| + | :<math>-3x-y+2z=-11 \ </math> | ||
| + | :<math>-2x+y+2z=-3 \ </math> | ||
A lap 2008. február 2., 00:40-kori változata
A Gauss-elimináció egy eljárás, amivel megtalálhatjuk egy lineáris egyenletrendszer megoldásait, meghatározhatjuk egy mátrix rangját.
Az eljárás során először a kibővített együtthatómátrixot elemi sorekvivalens átalakítások felhasználásával lépcsős alakúra hozzuk, majd a második lépésben redukált lépcsős alakra redukáljuk.
Az eljárás leírása
A lineáris egyenletrendszereket rendezhetjük úgy, hogy az egyenlőség jobb oldalára írjuk a konstansokat, a bal oldalára pedig rögzített sorrendben az ismeretleneket és az együtthatókat. Ha ezeket az együtthatókat és konstansokat táblázatba rendezzük, akkor kapjuk a kibővített együtthatómátrixot.
A kibővített együtthatómátrix akkor lépcsős alakú, ha minden sor az első nemnulla eleme 1 (vezéregyes), valamint bármely vezéregyes alatt csak tőle jobbra lévő oszlopban vannak vezéregyesek. A redukált lépcsős alak az olyan lépcsős alak aminél minden vezéregyes az egyetlen nemnulla elem az oszlopában.
A lineáris egyenletrendszer megoldásait nem változtatják meg az elemi sorekvivalens átalakítások:
- Sorok felcserélése
- Egy sor elemeinek nullától különböző számmal történő végigszorzása
- Egy sor konstansszorosának másikhoz való elemenkénti hozzáadása
Példa
Oldjuk meg az alábbi lineáris egyenletrendszert: