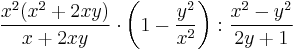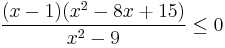Gyakorló első zh
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 9. sor: | 9. sor: | ||
'''4.''' Mennyi <math>\left(\dfrac{7}{\sqrt[4]{7}}\right)^{\log_{49}16}</math> | '''4.''' Mennyi <math>\left(\dfrac{7}{\sqrt[4]{7}}\right)^{\log_{49}16}</math> | ||
| − | '''5.''' <math>\dfrac{x^2(x^2+2xy)}{x+2xy}\cdot \left(1-\dfrac{y^2}{x^2}\right):\dfrac{x^2-y^2}{2y+1}</math> | + | '''5.''' Egy számtani sorozat 3., 7. és 9. tagjának összege öt, az 1., 8. és 10. tagjának összege nyolc. Melyik ez a számtani sorozat? |
| + | |||
| + | '''6.''' <math>\dfrac{x^2(x^2+2xy)}{x+2xy}\cdot \left(1-\dfrac{y^2}{x^2}\right):\dfrac{x^2-y^2}{2y+1}</math> | ||
A lap 2020. október 13., 22:33-kori változata
1. Oldja meg az alábbi egyenlőtlenséget!
2. Határozza meg az 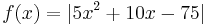 függvény szélsőértékeit és azok helyét!
függvény szélsőértékeit és azok helyét!
3. Határozza meg, hogy mely p értékre lesz az 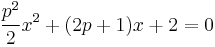 egyenletnek egyetlen megoldása! Mikor lesz mindkét gyök pozitív?
egyenletnek egyetlen megoldása! Mikor lesz mindkét gyök pozitív?
4. Mennyi ![\left(\dfrac{7}{\sqrt[4]{7}}\right)^{\log_{49}16}](/upload/math/d/0/e/d0ed523bbfbb4bc3002bae06920bc69a.png)
5. Egy számtani sorozat 3., 7. és 9. tagjának összege öt, az 1., 8. és 10. tagjának összege nyolc. Melyik ez a számtani sorozat?
6.