Haladó szintre hozó kurzus/1
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Kijelentéslogika) |
Mozo (vitalap | szerkesztései) (→Kijelentéslogika) |
||
| 8. sor: | 8. sor: | ||
:c) <math>q\Rightarrow (p\vee (\neg p))</math> (az "igaz" mindenből következik) | :c) <math>q\Rightarrow (p\vee (\neg p))</math> (az "igaz" mindenből következik) | ||
:d) <math>[(p\Rightarrow r) \wedge (q\Rightarrow r)\wedge (p\vee q)]\Rightarrow r</math> (az esetszétválasztás szabálya) | :d) <math>[(p\Rightarrow r) \wedge (q\Rightarrow r)\wedge (p\vee q)]\Rightarrow r</math> (az esetszétválasztás szabálya) | ||
| + | :e) <math>[\neg(p\Rightarrow q)\Rightarrow [(\neg q)\Rightarrow (\neg p)]</math> (a kontrapozíció szabálya) | ||
A lap 2016. június 28., 21:00-kori változata
- Ez az szócikk a Haladó szintre hozó szócikk alszócikke.
Kijelentéslogika
1. Igazoljuk igazságtáblázattal, hogy a következő kijelentések mindig igazak:
- a)
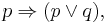
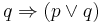 (a "vagy" alaptulajdonsága)
(a "vagy" alaptulajdonsága)
- b)
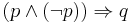 (a "hamisból" minden következik)
(a "hamisból" minden következik)
- c)
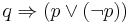 (az "igaz" mindenből következik)
(az "igaz" mindenből következik)
- d)
![[(p\Rightarrow r) \wedge (q\Rightarrow r)\wedge (p\vee q)]\Rightarrow r](/upload/math/a/f/6/af6a1f4b08d74a659f06d8ad51bd32e5.png) (az esetszétválasztás szabálya)
(az esetszétválasztás szabálya)
- e)
![[\neg(p\Rightarrow q)\Rightarrow [(\neg q)\Rightarrow (\neg p)]](/upload/math/a/f/5/af5abb1bb0c7446774b60049df2b93d6.png) (a kontrapozíció szabálya)
(a kontrapozíció szabálya)
| Haladó szintre hozó | 2. téma |