Informatics1-2019/Lab10
A MathWikiből
(Változatok közti eltérés)
a (→Server) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 23. sor: | 23. sor: | ||
## Use '''bool''' to convert to logical value | ## Use '''bool''' to convert to logical value | ||
## Is it true for real numbers? Positive numbers? ('''assume''') | ## Is it true for real numbers? Positive numbers? ('''assume''') | ||
| − | # Prove | + | # Prove <math>(x-y)(x+y) = x^2-y^2</math> |
| − | # Prove | + | # Prove <math>(-1)^{2n} = 1</math> where '''n''' is integer! |
=== Sage functions, methods === | === Sage functions, methods === | ||
| − | # Is | + | # Is 2019 a prime? (use the ''is_prime()'' function) |
| + | #* try to find a big prime number just by trial and error! | ||
# Were you born on a prime day? (use the D variable!) | # Were you born on a prime day? (use the D variable!) | ||
| − | # Solve the equation | + | # Solve the equation <math>Dx^2 + Mx - br = 0</math> using the ''solve(f, variable)'' function! |
| − | # Solve the equation numerically! Use the ''find_root( | + | #* ''x'' needs to be a symbolic variable! |
| + | #* ''f'' can be a function, formula or an equation. | ||
| + | # Solve the equation numerically! Use the ''find_root(f, min, max)'' function, where min and max defines an interval where Sage looks for the solution. | ||
| + | #* this only works is you have one variable! | ||
# Solve the above equation symbolically (make D, M, b, r symbolic variables, then use solve)! | # Solve the above equation symbolically (make D, M, b, r symbolic variables, then use solve)! | ||
| − | # Differentiate the function sin(x)cos(x)x^2. | + | # Differentiate the function <math>\sin(x)\cdot\cos(x)\cdot x^2</math>. |
# Integrate the previous function. | # Integrate the previous function. | ||
| − | # Calculate the limit of (1 + 3 | + | # Calculate the limit of <math>\lim_{n\to\infty}\bigg(1 + \frac{3}{n}\bigg)^{4n}</math> |
| − | # Let f be the following function: f = (x+2*y)^3 | + | # Let f be the following function: f(x,y) = (x+2*y)^3 |
# Substitute 3 into x; then 4 into x and 2 into y. What's the result? ( use the ''subs()'' method of f) | # Substitute 3 into x; then 4 into x and 2 into y. What's the result? ( use the ''subs()'' method of f) | ||
# Expand f! (''expand()'') | # Expand f! (''expand()'') | ||
| − | # Using the above, calculate the [https://en.wikipedia.org/wiki/Taylor_series Taylor series] of sin(x)cos(x)x^2 up until the 4th member. (you can differentiate and integrate a function '''f''' by '''f.diff(x)''') | + | # Using the above, calculate the [https://en.wikipedia.org/wiki/Taylor_series Taylor series] of <math>\sin(x)\cdot\cos(x)\cdot x^2</math> up until the 4th member. (you can differentiate and integrate a function '''f''' by '''f.diff(x)''') |
=== Plotting with Sage (plot) === | === Plotting with Sage (plot) === | ||
# Plot a cosine curve from 0 to 4*pi! | # Plot a cosine curve from 0 to 4*pi! | ||
| − | # Plot the (x-2)^2 + 3 polynomial from -2 to 4, color it green! | + | # Plot the <math>(x-2)^2 + 3</math> polynomial from -2 to 4, color it green! |
| − | # Plot next to the previous one (using the ''show'' function) the function x^3-3*x + 6 in red! | + | # Plot next to the previous one (using the ''show'' function) the function <math>x^3-3*x + 6</math> in red! |
# Plot a circle: ''cirlce((coordinates of the center), radius, optional)''. The "optional" can be: color, ''aspect_ratio=True'' so that the ratio of the x and y axis are kept, otherwise we might get an ellipse. | # Plot a circle: ''cirlce((coordinates of the center), radius, optional)''. The "optional" can be: color, ''aspect_ratio=True'' so that the ratio of the x and y axis are kept, otherwise we might get an ellipse. | ||
[[Informatics1-2019/Lab09|Previous]] - [[Informatics1-2019#Labs|Up]] - [[Informatics1-2019/Lab11|Next]] | [[Informatics1-2019/Lab09|Previous]] - [[Informatics1-2019#Labs|Up]] - [[Informatics1-2019/Lab11|Next]] | ||
A lap jelenlegi, 2019. december 2., 16:33-kori változata
Tartalomjegyzék |
Sage
Server
https://jupyter.math.bme.hu:8888/
You can log in with your leibniz username and password.
You can use this, or install it on your own from here: http://www.sagemath.org/
Tasks
Using variables
- Let Y be your year of birth, M the month, and D the day, create these variables.
- How much is Y divided by D? Associate this value with the b variable.
- Let r be the remainder of Y / M.
- What's the difference r - b?
Symbolic calculations
- Is it true that the square root of the square of a number is the number itself?
- Use bool to convert to logical value
- Is it true for real numbers? Positive numbers? (assume)
- Prove (x − y)(x + y) = x2 − y2
- Prove ( − 1)2n = 1 where n is integer!
Sage functions, methods
- Is 2019 a prime? (use the is_prime() function)
- try to find a big prime number just by trial and error!
- Were you born on a prime day? (use the D variable!)
- Solve the equation Dx2 + Mx − br = 0 using the solve(f, variable) function!
- x needs to be a symbolic variable!
- f can be a function, formula or an equation.
- Solve the equation numerically! Use the find_root(f, min, max) function, where min and max defines an interval where Sage looks for the solution.
- this only works is you have one variable!
- Solve the above equation symbolically (make D, M, b, r symbolic variables, then use solve)!
- Differentiate the function
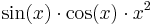 .
.
- Integrate the previous function.
- Calculate the limit of
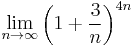
- Let f be the following function: f(x,y) = (x+2*y)^3
- Substitute 3 into x; then 4 into x and 2 into y. What's the result? ( use the subs() method of f)
- Expand f! (expand())
- Using the above, calculate the Taylor series of
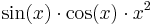 up until the 4th member. (you can differentiate and integrate a function f by f.diff(x))
up until the 4th member. (you can differentiate and integrate a function f by f.diff(x))
Plotting with Sage (plot)
- Plot a cosine curve from 0 to 4*pi!
- Plot the (x − 2)2 + 3 polynomial from -2 to 4, color it green!
- Plot next to the previous one (using the show function) the function x3 − 3 * x + 6 in red!
- Plot a circle: cirlce((coordinates of the center), radius, optional). The "optional" can be: color, aspect_ratio=True so that the ratio of the x and y axis are kept, otherwise we might get an ellipse.