Informatika1-2019/Gyakorlat10
Előző gyakorlat - Fel - Következő gyakorlat
Tartalomjegyzék |
MatLab feladatok
LER
Számoljuk ki az alábbi egyenletrendszerek összes megoldását, illetve állapítsuk meg, hogy van-e megoldásuk.
a
x + 5y = 1 2x + 4y = 2
b
x + 5y = 1 2x + 4y = 2 5x - 6y = -1
c
x + 2y + 5z = 1 5x + 4y + 6z = 2
Írjuk meg a fenti általános LER megoldót egy függvénybe!
Trükkös mátrix
Állítsuk elő az alábbi mátrixot:
1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 11
3 4 5 6 7 8 9 10 11 12
4 5 6 7 8 9 10 11 12 13
5 6 7 8 9 10 11 12 13 14
6 7 8 9 10 11 12 13 14 15
7 8 9 10 11 12 13 14 15 16
8 9 10 11 12 13 14 15 16 17
9 10 11 12 13 14 15 16 17 18
10 11 12 13 14 15 16 17 18 19
szorzótábla
Készítsünk modulo-7 szorzótáblát:
0 0 0 0 0 0 0
0 1 2 3 4 5 6
0 2 4 6 1 3 5
0 3 6 2 5 1 4
0 4 1 5 2 6 3
0 5 3 1 6 4 2
0 6 5 4 3 2 1
általánosan
Készítsünk függvényt, ami egy adott n számra elkészíti a modulo-n szorzótáblát, de csak ha n prím szám. Ha nem prím, adjon vissza egy 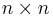 -es csupa nulla mátrixot.
-es csupa nulla mátrixot.
isprime
Összegzések
a
Írjunk olyan függvényt, ami térbeli pontoknak meghatározza a súlypontját. Ehhez generáljunk egy 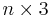 -as véletlen mátrixot, melynek minden sora egy 3-dimenziós pontot reprezentál.
Ez legyen a függvény bemenete. Kimenete pedig egy
-as véletlen mátrixot, melynek minden sora egy 3-dimenziós pontot reprezentál.
Ez legyen a függvény bemenete. Kimenete pedig egy
a
Írjunk olyan függvényt, ami egy mátrixnak kiszámolja az elemeinek abszolút értékének átlagát
b
Írjunk olyan függvényt, ami egy mátrixnak kiszámolja az elemeinek abszolút értékének soronkénti összegének maximumát.
| M = maxi | ∑ | | Ai,j | |
| j |
c
Írjunk olyan függvényt, ami egy mátrixnak kiszámolja az elemeinek abszolút értékének oszloponkénti összegének maximumát.
| m = maxj | ∑ | | Ai,j | |
| i |