Informatika1-2019/Gyakorlat11
a (→A program használata) |
|||
| 112. sor: | 112. sor: | ||
## Használjuk a '''bool''' függvényt, ami az igazságértékét meghatározza egy kifejezésnek | ## Használjuk a '''bool''' függvényt, ami az igazságértékét meghatározza egy kifejezésnek | ||
## valós számokra igaz? Pozitív számokra? ('''assume''') | ## valós számokra igaz? Pozitív számokra? ('''assume''') | ||
| − | # Lássuk be, hogy | + | # Lássuk be, hogy <math>(x-y)(x+y) = x^2-y^2</math> |
| − | # Lássuk be, hogy | + | # Lássuk be, hogy <math>(-1)^{2n} = 1</math>, de persze csak ha '''n''' egész! |
=== Beépített Sage függvények, metódusok === | === Beépített Sage függvények, metódusok === | ||
| 119. sor: | 119. sor: | ||
# Prímszám-e 2011? (használd az ''is_prime()'' függvényt) | # Prímszám-e 2011? (használd az ''is_prime()'' függvényt) | ||
# Prímedik napján születtél-e a hónapnak? (használd a D változót!) | # Prímedik napján születtél-e a hónapnak? (használd a D változót!) | ||
| − | # Oldd meg a | + | # Oldd meg a <math>Dx^2 + Mx - br = 0</math> egyenletet a ''solve(fv, változó)'' függvény segítségével! |
| + | #* ''x'' szimbolikus változó kell legyen! | ||
| + | #* ''fv'' lehet függvény, kifejezés vagy egyenlet | ||
# Numerikusan is oldd meg az egyenletet! Használd a ''find_root(fv == 0, min, max)'' függvényt. Egy változós függvény egyetlen változójában keres megoldást. | # Numerikusan is oldd meg az egyenletet! Használd a ''find_root(fv == 0, min, max)'' függvényt. Egy változós függvény egyetlen változójában keres megoldást. | ||
# Oldd meg a fenti egyenletet szimbolikusan is (fejezd ki x-et b, D, M és r-rel)! | # Oldd meg a fenti egyenletet szimbolikusan is (fejezd ki x-et b, D, M és r-rel)! | ||
| − | # Deriváld le az sin(x)cos(x)x^2 függvényt. | + | # Deriváld le az <math>\sin(x)\cdot\cos(x)\cdot x^2</math> függvényt. |
# Integráld le az elõzõ függvényt. | # Integráld le az elõzõ függvényt. | ||
| − | # Számold ki | + | # Számold ki az alábbi határértéket: <math>\lim_{n\to\infty}\bigg(1 + \frac{3}{n}\bigg)^{4n}</math> |
| − | # Legyen f a következő függvény: f = (x+2*y)^3 | + | (''limit'', de az ''n''-nek változónak kell lennie) |
| + | # Legyen f a következő függvény: f(x,y) = (x+2*y)^3 | ||
# Helyettesíts be x helyére 3-at; utána x helyére 4-et és y helyére 2-t. Mennyi az eredmény? ( használd f-nek a ''subs()'' függvényét) | # Helyettesíts be x helyére 3-at; utána x helyére 4-et és y helyére 2-t. Mennyi az eredmény? ( használd f-nek a ''subs()'' függvényét) | ||
# Bontsd összeggé f-et! (''expand()'') | # Bontsd összeggé f-et! (''expand()'') | ||
| − | # Az elõbb tanultakat használva, számold ki az 4. tagig a sin(x)cos(x)x^2 függvény [https://hu.wikipedia.org/wiki/Taylor-sor Taylor-sorát] (deriválni / integrálni, ha '''f''' egy függvény úgy is lehet, hogy '''f.diff(x)''') | + | # Az elõbb tanultakat használva, számold ki az 4. tagig a <math>\sin(x)\cdot\cos(x)\cdot x^2</math> függvény [https://hu.wikipedia.org/wiki/Taylor-sor Taylor-sorát] (deriválni / integrálni, ha '''f''' egy függvény úgy is lehet, hogy '''f.diff(x)''') |
=== Rajzolás a Sage segítségével (plot) === | === Rajzolás a Sage segítségével (plot) === | ||
| − | # Rajzolj egy cosinus-görbét 0-tól 4 | + | # Rajzolj egy cosinus-görbét 0-tól <math>4\pi</math>-ig! |
| − | # Rajzold ki az (x-2)^2 + 3 másodfokú polinomot -2-től 4-ig, zöld színnel! | + | # Rajzold ki az <math>(x-2)^2 + 3</math> másodfokú polinomot -2-től 4-ig, zöld színnel! |
| − | # Rajzold az előző mellé (a ''show'' függvénnyel) az x^3-3*x + 6 harmadfokú polinomot pirossal! | + | # Rajzold az előző mellé (a ''show'' függvénnyel) az <math>x^3-3*x + 6</math> harmadfokú polinomot pirossal! |
# Rajzoljunk kört: ''circle((középpont koordinátái), sugár, egyebek)''. Az "egyebek" lehetnek: szín, ''aspect_ratio=True'' hogy az x és y tengelyek skálázása azonos legyen (különben ellipszist kaphatunk!). | # Rajzoljunk kört: ''circle((középpont koordinátái), sugár, egyebek)''. Az "egyebek" lehetnek: szín, ''aspect_ratio=True'' hogy az x és y tengelyek skálázása azonos legyen (különben ellipszist kaphatunk!). | ||
[[Informatika1-2019/Gyakorlat10|Előző gyakorlat]] - [[Informatika1-2019#Gyakorlatok|Fel]] - [[Informatika1-2019/Gyakorlat12|Következő gyakorlat]] | [[Informatika1-2019/Gyakorlat10|Előző gyakorlat]] - [[Informatika1-2019#Gyakorlatok|Fel]] - [[Informatika1-2019/Gyakorlat12|Következő gyakorlat]] | ||
A lap 2019. december 2., 16:31-kori változata
Előző gyakorlat - Fel - Következő gyakorlat
Tartalomjegyzék |
A program használata
Az intézeti szerver
https://jupyter.math.bme.hu:8888/
Publikus
Otthonról
Telepíthetjük a saját gépünkre: http://www.sagemath.org/download.html
parancssorból
A leibniz-en írjuk be parancssorba, hogy sage, ekkor megnyílik a sage interactive shell.
Ide már írhatunk be sage parancsokat, például:
23^19
Help
online dokumentáció: https://doc.sagemath.org/html/en/reference/
Alternatíva
A Sage maga a Mathematica program egy alternatívája. A Mathematica program Stephen Wolfram szüleménye, 1988-ből. Azóta is folyamatosan fejlesztik és fejlődik. Ez egy fizetős program, de a matematikus hallgatók kaphatnak hozzáférést az intézet jóvoltából.
Telepíthetjük egy aktivációs kulccsal. Letöltés: http://math.bme.hu/mathematica
Feladatok
- Számold ki 2018 négyzetgyökét!
- Számold ki 2018 negyedik gyökét!
- Számold ki 2018 hatodik hatványát!
- Mennyi 123*321-nek a 11-es maradéka?
Kiegészítés és help
A sage okosan ki tudja egészíteni a parancsainkat, próbáljuk meg a következőt:
V = Vec[nyomjunk TAB-ot]
Ekkor egyrészt kiegészíti Vector-ig, másrészt kiírja a lehetséges parancsokat. Egészítsük ki, hogy a következőt kapjuk:
V = VectorSpace(QQ,3)
Ezzel V-t a racionális test feletti 3 dimenziós vektortérnek definiáltuk.
Írjuk be most, hogy V. és nyomjunk TAB-ot. Felsorolja az összes lehetséges műveletet, amit V-n tudunk végezni. Ha a parancs végére egy kérdőjelet teszünk, akkor egy rövid leírást is ad róla, hogy mit csinál. Például:
V.basis?
Le is futtathatjuk a parancsot:
V.basis()
Sage notebook
- Menjünk a sage notebook oldalára: https://jupyter.math.bme.hu:8888/
- Itt lépjünk be a leibniz-es felhasználónevünkkel és a jelszóval
- New -> SageMath 8.9 gombokkal lehet új sage notebook-ot létrehozni
- A bal-fenti sarokban, a logó mellett lehet átnevezni a notebbok-ot (kezdetben Untitled lesz a neve)
Első próbálkozások
- A cellákba írhatunk sage parancsokat, akár többet is. Próbáljuk is ki:
A = Matrix([[1, 1], [1, 0]]) B = Matrix([[-2, 0], [-1, 1]])
- SHIFT + ENTER-el tudjuk lefuttatni a parancsokat. Ekkor sorban futnak le egymás után az egy cellában levő parancsok.
- A cella legutolsó művelete íródik ki, ha nem csak a legutolsót akarjuk kiírni, akkor használjunk print-et.
- Próbáljuk ki, hogy egy új cellába beírjuk, hogy A vagy B és lefuttatjuk. Majd próbáljuk ki az A*B-t.
Szimbolikus változók
x = var('x') y = var('y') x^2 + y^2
Egy változó lehet numerikus (konkrét érték) és szimbolikus is.
y = 2 x^2 + y^2
Függvények
Ha x egy változó, akkor egyszerűen
f(x) = x^2 print(f(3)) print(f(y))
Feladatok
Változók használata
- Legyen Y a születési éved, M a születési hónapod, és D a születésed napja, ezekhez vedd fel a három változót.
- Hányszor van meg D Y-ban? Legyen az érték a b változóhoz rendelve.
- Legyen r a születési évednek a hónappal vett maradéka.
- Mennyi most b és r különbsége?
Szimbolikus számítások
- Igaz-e, hogy egy szám négyzetének gyöke maga a szám?
- Használjuk a bool függvényt, ami az igazságértékét meghatározza egy kifejezésnek
- valós számokra igaz? Pozitív számokra? (assume)
- Lássuk be, hogy (x − y)(x + y) = x2 − y2
- Lássuk be, hogy ( − 1)2n = 1, de persze csak ha n egész!
Beépített Sage függvények, metódusok
- Prímszám-e 2011? (használd az is_prime() függvényt)
- Prímedik napján születtél-e a hónapnak? (használd a D változót!)
- Oldd meg a Dx2 + Mx − br = 0 egyenletet a solve(fv, változó) függvény segítségével!
- x szimbolikus változó kell legyen!
- fv lehet függvény, kifejezés vagy egyenlet
- Numerikusan is oldd meg az egyenletet! Használd a find_root(fv == 0, min, max) függvényt. Egy változós függvény egyetlen változójában keres megoldást.
- Oldd meg a fenti egyenletet szimbolikusan is (fejezd ki x-et b, D, M és r-rel)!
- Deriváld le az
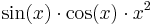 függvényt.
függvényt.
- Integráld le az elõzõ függvényt.
- Számold ki az alábbi határértéket:
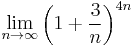
(limit, de az n-nek változónak kell lennie)
- Legyen f a következő függvény: f(x,y) = (x+2*y)^3
- Helyettesíts be x helyére 3-at; utána x helyére 4-et és y helyére 2-t. Mennyi az eredmény? ( használd f-nek a subs() függvényét)
- Bontsd összeggé f-et! (expand())
- Az elõbb tanultakat használva, számold ki az 4. tagig a
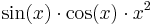 függvény Taylor-sorát (deriválni / integrálni, ha f egy függvény úgy is lehet, hogy f.diff(x))
függvény Taylor-sorát (deriválni / integrálni, ha f egy függvény úgy is lehet, hogy f.diff(x))
Rajzolás a Sage segítségével (plot)
- Rajzolj egy cosinus-görbét 0-tól 4π-ig!
- Rajzold ki az (x − 2)2 + 3 másodfokú polinomot -2-től 4-ig, zöld színnel!
- Rajzold az előző mellé (a show függvénnyel) az x3 − 3 * x + 6 harmadfokú polinomot pirossal!
- Rajzoljunk kört: circle((középpont koordinátái), sugár, egyebek). Az "egyebek" lehetnek: szín, aspect_ratio=True hogy az x és y tengelyek skálázása azonos legyen (különben ellipszist kaphatunk!).