Informatika1-2019/HF6
A MathWikiből
(Változatok közti eltérés)
(Új oldal, tartalma: „= MatLab házi feladat = '''(6 pont)''' A feladat két MatLab függvény megírása lesz, két <tt>.m</tt> fájlt kell beküldeni, a fájlok neve kezdődjön így: '''…”) |
a (→Mágikus mátrix (3 pont)) |
||
| 9. sor: | 9. sor: | ||
Példa: | Példa: | ||
| + | |||
| + | >> magicmatrix(12,11) | ||
1 1 0 0 0 0 1 1 0 0 0 | 1 1 0 0 0 0 1 1 0 0 0 | ||
0 0 1 1 0 0 0 0 1 1 0 | 0 0 1 1 0 0 0 0 1 1 0 | ||
| 21. sor: | 23. sor: | ||
0 0 1 1 0 0 0 0 1 1 0 | 0 0 1 1 0 0 0 0 1 1 0 | ||
0 0 0 0 1 1 0 0 0 0 1 | 0 0 0 0 1 1 0 0 0 0 1 | ||
| − | + | ||
== Eliminálás (3 pont) == | == Eliminálás (3 pont) == | ||
Írjunk <tt>eliminal</tt> nevű függvényt, aminek négy argumentuma van | Írjunk <tt>eliminal</tt> nevű függvényt, aminek négy argumentuma van | ||
A lap 2019. december 2., 23:08-kori változata
Tartalomjegyzék |
MatLab házi feladat
(6 pont)
A feladat két MatLab függvény megírása lesz, két .m fájlt kell beküldeni, a fájlok neve kezdődjön így: <tankör>_HF<a feladat száma>_<felhasználói név>
Mágikus mátrix (3 pont)
Írjunk magicmatrix nevű függvényt, aminek két argumentuma van, két pozitív egész szán: n és m.
Eredménye egy 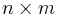 -es mátrix legyen, amiben oldalra kettő, lefele egy mintázatban követik egymást az egyesek, minden harmadik sorból indulva, mindenhol máshol 0-k legyenek.
-es mátrix legyen, amiben oldalra kettő, lefele egy mintázatban követik egymást az egyesek, minden harmadik sorból indulva, mindenhol máshol 0-k legyenek.
Példa:
>> magicmatrix(12,11) 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1
Eliminálás (3 pont)
Írjunk eliminal nevű függvényt, aminek négy argumentuma van
- egy mátrix
- három pozitív szám: i, j, k
A három pozitív szám két sor index és egy oszlop index. A függvény eredménye egy olyan mátrix, mint az első argumentum, de az i-edik sor k-adik elemével nullázzuk ki a j-edik sor k-adik elemét.
Például
M =
1 2 3
4 5 6
7 8 9
>> eliminal(M, 1, 2, 1)
ans =
1 2 3
0 -3 -6
7 8 9
>> eliminal(eliminal(M, 1, 2, 1), 1, 3, 1)
ans =
1 2 3
0 -3 -6
0 -6 -12
>> eliminal(eliminal(eliminal(M, 1, 2, 1), 1, 3, 1), 2, 3, 2)
ans =
1 2 3
0 1 2
0 0 0
>> eliminal(eliminal(eliminal(eliminal(M, 1, 2, 1), 1, 3, 1), 2, 3, 2), 3, 2, 3)
ans =
1 2 3
0 1 2
0 0 0
>> eliminal(eliminal(eliminal(eliminal(M, 1, 2, 1), 1, 3, 1), 2, 3, 2), 2, 1, 2)
ans =
1 0 -1
0 1 2
0 0 0
- Ha az i-edik sor k-adik eleme nulla, ugyanaz a mátrix legyen az eredmény, mint ami a bemenet.
- Ha nem nulla, akkor
- Osszuk le az i-edik sort annyival, hogy az i-edik sor k-adik elem 1 legyen
- A j-edik sorból vonjuk ki az i-edik sor annyiszorosát, hogy a j-edik sor k-adik eleme 0 legyen
Határidő
2019. december 8., 23:59:59