Informatika2-2012/Hazi03
| 1. sor: | 1. sor: | ||
=== 3. házi feladat: Polinomok tömbök segítségével === | === 3. házi feladat: Polinomok tömbök segítségével === | ||
| − | Írjunk programot, mely | + | Írjunk programot, mely kiszámolja egy legföljebb 10-edfokú polinom fokát és helyettesítési értékét! |
| − | + | A polinomokat egyszerűen együtthatóinak tömbjeként kezeljük, | |
például a <math>p_1(x) = x^3 - 5x + 12</math> polinomot egy olyan p1 nevű | például a <math>p_1(x) = x^3 - 5x + 12</math> polinomot egy olyan p1 nevű | ||
| − | tömbbel | + | tömbbel adhatjuk meg, melynek elemei: <code>p1[0]=12</code>, |
<code>p1[1]=-5</code>, <code>p1[2]=0</code>, | <code>p1[1]=-5</code>, <code>p1[2]=0</code>, | ||
<code>p1[3]=1</code>, <code>p1[4]=0</code>,... <code>p1[10]=0</code>. | <code>p1[3]=1</code>, <code>p1[4]=0</code>,... <code>p1[10]=0</code>. | ||
A lap 2012. február 25., 19:05-kori változata
3. házi feladat: Polinomok tömbök segítségével
Írjunk programot, mely kiszámolja egy legföljebb 10-edfokú polinom fokát és helyettesítési értékét!
A polinomokat egyszerűen együtthatóinak tömbjeként kezeljük,
például a p1(x) = x3 − 5x + 12 polinomot egy olyan p1 nevű
tömbbel adhatjuk meg, melynek elemei: p1[0]=12,
p1[1]=-5, p1[2]=0,
p1[3]=1, p1[4]=0,... p1[10]=0.
Írjunk két függvényt a main-en kívül:
1. Az egyik függvény legyen az, amely megállapítja, és értékként visszaadja egy polinom fokát! Ennek deklarációja lehet például a következő:
int fok( float polinom[] );
hívása például fok( p1 ), ahol p1 egy már definiált polinom.
Az algoritmus egyszerűen keresse meg a legnagyobb indexű nemnulla
értéket a polinomot megadó tömbben. Az azonosan nulla polinom fokát
mínusz végtelennek szokás definiálni, ekkor e függvény adja vissza az
ábrázolható legkisebb egészt! E függvényhez el kell tudnunk dönteni, hogy egy
lebegőpontosan ábrázolt szám egyenlő-e nullával. A számábrázolás
pontatlansága miatt az (a == 0.0) feltétel nem lesz jó, ezért egy
számról akkor fogjuk azt mondani, hogy 0, ha valamely előre megadott
EPSILON értéknél abszolút értékben kisebb. Lehet például EPSILON = 1e-10, vagyis 10 − 10. Használjuk az alábbi kódot (vagy helyettesítsük egy jobbal):
int kbNulla( float a ){ float EPSILON=1e-10; if ( a < EPSILON && a > -EPSILON ) return 1; return 0; }
2. Írjunk egy függvényt, mely kiszámolja egy polinom értékét egy megadott helyen a Horner-módszert használva. A Horner-módszer az
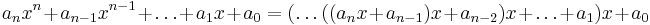
összefüggésre épül, mellyel hatványozás nélkül, és gyorsan értékelhető ki egy polinom. Ha e függvény deklarációja
float Horner( float polinom[], float x );
akkor például a fent megadott p1 polinom és x=1.0 esetén a
Horner( p1, x ) függvényhívás 8.0-át ad vissza. E függvényben használjuk a fokszámot megadó függvényt.
A programunkat kezdjük az alábbi sorokkal:
#include <stdio.h> #include <limits.h> #define MAX_POL 11 // minden polinomon legföljebb 10-edfokú
Az utolsó sorban egy konstanst definiáltunk. Ez a makróparancs a fordítás első fázisában a kód a MAX_POL változó helyébe 11-et helyettesít.
A main függvényben az alábbi polinomokat definiáljuk, és mindegyiknek
írjuk ki a fokát és a helyettesítési értékét az x = 1.2 helyen!
int main(void){ float p1[MAX_POL]={12,-5,0,1,0,0,0,0,0,0,0}; float p2[MAX_POL]={1,0,0,0,0,0,0,0,0,0,1}; float p3[MAX_POL]={5,0,0,0,0,0,0,0,0,0,0}; float p4[MAX_POL]={0,0,0,0,0,0,0,0,0,0,0};
A két függvény és a kbNulla függvény mindegyikét a main előtt
deklaráljuk, és a main után definiáljuk!