Informatika2-2016/Gyakorlat13
A MathWikiből
(Változatok közti eltérés)
(→Feladatok) |
(→Gradiens módszer) |
||
| 16. sor: | 16. sor: | ||
==Gradiens módszer== | ==Gradiens módszer== | ||
Egy kétváltozós függvény minimumát a következőképp közelítjük. Elindulunk egy <math>(x_0,y_0)</math> pontból, majd <math>\nabla f(x,y)\cdot \epsilon</math>-t kivonunk belőle. Ezt csináljuk addig, amíg a lépés abszolútértéke 0.0001 alatt nem lesz. Írjuk meg numpy segítségével az <math>f(x,y)=x^2+y^2</math> függvény minimumkeresését! <math>\epsilon = 0.01, (x_0,y_0)=(-1,-1)</math>! | Egy kétváltozós függvény minimumát a következőképp közelítjük. Elindulunk egy <math>(x_0,y_0)</math> pontból, majd <math>\nabla f(x,y)\cdot \epsilon</math>-t kivonunk belőle. Ezt csináljuk addig, amíg a lépés abszolútértéke 0.0001 alatt nem lesz. Írjuk meg numpy segítségével az <math>f(x,y)=x^2+y^2</math> függvény minimumkeresését! <math>\epsilon = 0.01, (x_0,y_0)=(-1,-1)</math>! | ||
| + | * Tároljuk el a lépéseket egy tömbben és plotoljuk ki a pontokat a matplotlib segítségével! | ||
| + | ==Gauss-elimináció kézzel== | ||
| + | Oldjuk meg Gauss-eliminációval az <math>3x_1-x_2+x_3-x_4+2x_5=13, x_1-2x_2+3x_3-x_4=5</math> | ||
A lap 2016. május 12., 07:45-kori változata
Tartalomjegyzék |
Feladatok
Előadás
Bevezető
Ismerkedésképp néhány egyszerű feladat.
- Hozzunk létre egy 10 hosszú, csupa 0 vektort! Módosítsuk a 4. elemét 1-re! (zeros)
- Hozzunk létre egy 3x3-as mátrixot, 0-tól 8-ig növekvő számokkal! (reshape)
- Hozzunk létre egy 30 hosszú listát véletlen számokkal 0 és 1 között! Számoljuk ki az elemek átlagát és a szórását! (rand, mean, std)
- Hozzunk lérte egy 30 hosszú listát véletlen számokkal -3 és 2 között!
- Hozzunk létre egy véletlen, 5 dimenziós egységvektort! Először egy véletlen vektor, majd gondoskodjunk róla, hogy egység hosszú legyen!
Monte-Carlo
Generáljunk 500,000 véletlen pontot a ![[0,2]\times[0,4]](/upload/math/d/1/f/d1f4d6baafac79655f4052ed2930bf35.png) téglalapba. Szánoljuk meg, hogy hány olyan (x,y) pont van, ahol x2 < y. Ez alapján becsüljük meg az
téglalapba. Szánoljuk meg, hogy hány olyan (x,y) pont van, ahol x2 < y. Ez alapján becsüljük meg az 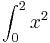 értékét! Segítség az előadás végén.
értékét! Segítség az előadás végén.
- Most ugyanezt csináljuk meg, csak a véletlent zárjuk ki belőle! Osszuk fel a [0,2] és a [0,4] intervallumokat egyenletesen a linspace függvénnyel. A meshgrid és a ravel segítségével létrehozzuk a
![[0,2]\times[0,4]](/upload/math/d/1/f/d1f4d6baafac79655f4052ed2930bf35.png) rácspontjait. Most ezekre a pontokra csináljuk meg a Monte-Carlot!
rácspontjait. Most ezekre a pontokra csináljuk meg a Monte-Carlot!
Numerikus integrál
Számoljuk ki az 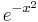 függvény integrálját a [ − 2,5]intervallumon téglalap módszerrel!
függvény integrálját a [ − 2,5]intervallumon téglalap módszerrel!
Gradiens módszer
Egy kétváltozós függvény minimumát a következőképp közelítjük. Elindulunk egy (x0,y0) pontból, majd 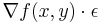 -t kivonunk belőle. Ezt csináljuk addig, amíg a lépés abszolútértéke 0.0001 alatt nem lesz. Írjuk meg numpy segítségével az f(x,y) = x2 + y2 függvény minimumkeresését! ε = 0.01,(x0,y0) = ( − 1, − 1)!
-t kivonunk belőle. Ezt csináljuk addig, amíg a lépés abszolútértéke 0.0001 alatt nem lesz. Írjuk meg numpy segítségével az f(x,y) = x2 + y2 függvény minimumkeresését! ε = 0.01,(x0,y0) = ( − 1, − 1)!
- Tároljuk el a lépéseket egy tömbben és plotoljuk ki a pontokat a matplotlib segítségével!
Gauss-elimináció kézzel
Oldjuk meg Gauss-eliminációval az 3x1 − x2 + x3 − x4 + 2x5 = 13,x1 − 2x2 + 3x3 − x4 = 5