Informatika2-2016/Gyakorlat14
A MathWikiből
A lap korábbi változatát látod, amilyen Nyida (vitalap | szerkesztései) 2016. május 19., 08:43-kor történt szerkesztése után volt.
Tartalomjegyzék |
Feladatok
Bevezető
- Írjunk egy fixed_point nevű függvényt, ami két paramétert kap: egy f függvényt és egy x0 értéket! Az f-et iteratívan hattatva az x0 kiindulópontból keressük meg a függvény fixpontját. Álljunk meg, ha a lépés kisebb mint 0.00001.
- Oldjuk meg, hogy legyen egy tol opcionális paramétere a függvénynek, 0.00001 alapértelmezett értékkel. Ezzel a megállási pontosságot lehessen megadni!
- Adjunk hozzá egy maxiter opcionális paramétert (default: 200), amivel limitálhatjuk az iterációk számát!
Ferde hajítás
Szimuláljuk a ferde hajítást közegellenállással. A közegellenállási erő mindig a sebességgel ellentéte irányú, 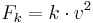 , ahol a k egy összetett paraméter, de ezzel most nem törődünk, csak állítgatjuk. A test kezdetben az x0 = (0,0) pontban van, sebessége pedig v0 = (vx,vy) (ezt mi adjuk majg meg lehet változtatni). Legyen egy epszilon változónk, mondjuk 0.01, ez lesz a lépéköz. Minden lépésben
, ahol a k egy összetett paraméter, de ezzel most nem törődünk, csak állítgatjuk. A test kezdetben az x0 = (0,0) pontban van, sebessége pedig v0 = (vx,vy) (ezt mi adjuk majg meg lehet változtatni). Legyen egy epszilon változónk, mondjuk 0.01, ez lesz a lépéköz. Minden lépésben  vektorral elmozdítjuk a testet, majd a sebességét csökkentjük
vektorral elmozdítjuk a testet, majd a sebességét csökkentjük 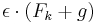 -vel (g a gravitációs gyorsulás, konstans [0,9.81] vektor). Tároljuk ez a mozgás pontjait addig, amíg újra nem ér földet a test és rajzoljuk ki!
-vel (g a gravitációs gyorsulás, konstans [0,9.81] vektor). Tároljuk ez a mozgás pontjait addig, amíg újra nem ér földet a test és rajzoljuk ki!
Fraktál fa
- Töltsük le a fractree.py file-t és futtassuk le!
- Próbáljuk meg nagyvonalakban megérteni a kódot, nem kell érteni minden számolást, csak azt, hogy kb hol mi történik.
- Módosítsuk a kódot, hogy többször ágazzon el (mondjuk 5 jó szám, annál többel már lehet lassú lesz).
- Elég uncsi, hogy mindig ugyanazt a fát rajzolja ki. Módosítuk, hogy az elágazás szöge (branchAngle) véletlen szám legyen [0, pi / 2] intervallumon.
- Csináljuk meg ugyanezt a törzs arányával is (trunkRatio), legyen mondjuk [0.25, 0.75] intervallumon véletlen szám!
- Elég uncsi még mindig, mert még mindig nagyon szimmetrikus, érjük most el, hogy a két ág más szög szerint ágazzon el:
- Csináljunk a branchAngle helyett branchAngleA és branchAngleB változókat, legyenek randomok mint a branchAngle volt.
- Cseréljük le a tree függvényben a pB és pC pontok létrehozásakor a branchAngle-t, az újonnan létrehozottakra, de az egyiknél az egyikre, másiknál a másikra!
- Az utolsó probléma már csak az, hogy még így is túl szabályosnak tûnik, mert a szögek állandóak, érjük el, hogy ágazás közben változzanak:
- A tree függvény végén növeljük a branchAngleA, branchAngleB és trunkRatio változókat egy véletlen számmal, mondjuk [-0.02, 0.02] közöttivel.
- Ahhoz, hogy ez mûködjön globálissá kell tenni a függvényben ezeket a változókat, szóval írjuk be a tree függvény elejére, hogy:
def tree(p0, p1, limit): global branchAngleA global branchAngleB global trunkRatio ...
- Próbáljunk olyan beállításokat találni, ami nekünk szimpatikus fát rajzol!
Sudoku
Megoldunk egy sudokut. Először a lenti kód kell.
def check_value(board, i, j, n): board[i,j] = n square = board[i/3:i/3+1,j/3:j/3+1].ravel() row = board[i,:].ravel() column = board[:,j].ravel() square_ok = np.bincount(square)[1:].max() <= 1 row_ok = np.bincount(row)[1:].max() <= 1 column_ok = np.bincount(column)[1:].max() <= 1 board[i,j] = 0 return square_ok and row_ok and column_ok def check_board(board): . . . def display(board): for i in range(9): if i in [3, 6]: print '------+-------+------' for j in range(9): if j in [3, 6]: print '|', print board[i,j], print board = np.array([[5,1,7,6,0,0,0,3,4], [2,8,9,0,0,4,0,0,0], [3,4,6,2,0,5,0,9,0], [6,0,2,0,0,0,0,1,0], [0,3,8,0,0,6,0,4,7], [0,0,0,0,0,0,0,0,0], [0,9,0,0,0,0,0,7,8], [7,0,3,4,0,0,5,6,0], [0,0,0,0,0,0,0,0,0]])