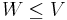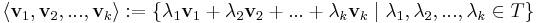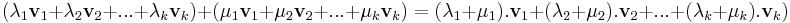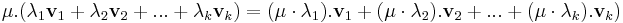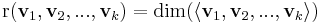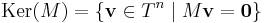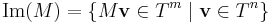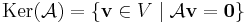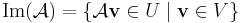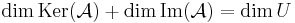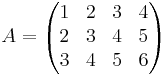Lineáris altér

A MathWikiből

(Változatok közti eltérés)

A lap 2008. március 3., 22:58-kori változata

A V vektortér lineáris alterének nevezzük a W ⊆ V halmazt, ha W vektorteret alkot ugyanazokkal a műveletekkel, melyek V-nek is műveletei. Azt, hogy W altere V-nek a következőképpen jelöljük:

$W\leq V\,$

Altér jellemzése

Annak ellenőrzése, hogy egy vektortér részhalmaza altér egyszerűbben türténik annál, minthogy ellenőrizzük, hogy a részhalmazra teljesülnek-e a vektortéraxiómák. Altér jellemezhető a következőkkel.

Tétel - Ha (V,+,.) vektortér a T test fölött és a W ⊆ V nemüres halmaz, akkor az alábbi két kijelentés ekvivalens egymással:

W altere V-nek
minden u, v ∈ W-re és λ ∈ T-re:

u + v ∈ W
λ.v ∈ W

Tehát altér, ami zárt az összeadásra és a számmal való szorzásra.

Példák

Triviális alterek

Bármely V vektortérben maga V és a nullvektort tartalmazó {0} halmaz altér. Az előbbi dim V dimenziós, az utóbbi nulladimenziós.

Generált altér

Ha v₁, v₂, ... ,v_k véges vektorrendszer a T test feletti V lineáris térben, akkor a

$\langle\mathbf{v}_1,\mathbf{v}_2,...,\mathbf{v}_k\rangle:=\{\lambda_1\mathbf{v}_1+\lambda_2\mathbf{v}_2+...+\lambda_k\mathbf{v}_k\mid \lambda_1,\lambda_2,..., \lambda_k\in T\}$

részhalmazát V-nek a { v₁, v₂, ... ,v_k } vektorrendszer által generált altérnek vagy kifeszített altérnek nevezünk.

Ez valóban altér, hiszen bármely két elemének összege és számszorosa eleme az részhalmaznak:

$(\lambda_1\mathbf{v}_1+\lambda_2\mathbf{v}_2+...+\lambda_k\mathbf{v}_k)+(\mu_1\mathbf{v}_1+\mu_2\mathbf{v}_2+...+\mu_k\mathbf{v}_k)=(\lambda_1+\mu_1).\mathbf{v}_1+(\lambda_2+\mu_2).\mathbf{v}_2+...+(\lambda_k+\mu_k).\mathbf{v}_k)$

$\mu.(\lambda_1\mathbf{v}_1+\lambda_2\mathbf{v}_2+...+\lambda_k\mathbf{v}_k)=(\mu\cdot\lambda_1).\mathbf{v}_1+(\mu\cdot\lambda_2).\mathbf{v}_2+...+(\mu\cdot\lambda_k).\mathbf{v}_k)$

Az vektorrendszer rangján éretjük, a vektorrendszer által kifesztett altér dimenzióját:

$\mathrm{r}(\mathbf{v}_1,\mathbf{v}_2,...,\mathbf{v}_k)=\mathrm{dim}(\langle\mathbf{v}_1,\mathbf{v}_2,...,\mathbf{v}_k\rangle)$

Mátrix magtere és képtere

Ha T test és M ∈ T^n×m, azaz n × m-es mártix, akkor

$\mathrm{Ker}(M)=\{\mathbf{v}\in T^n\mid M\mathbf{v}=\mathbf{0}\}$

az M mártix magtere, azaz azon elemek a Tⁿ vektortérből, melyeket a mátrix a vele való szorzás által a nullába visz és

$\mathrm{Im}(M)=\{M\mathbf{v}\in T^m\mid \mathbf{v}\in T^n\}$

az M képtere, azaz azon vektorok, melyek előállnak valamely vektor és az M mátrix szorzataként.

Praktikusan:

Ker(M) az M együtthatómátrixú homogén lineáris egyenletrendszer megoldásainak halmaza

Im(M) azon "jobb oldalak" halmaza az Mx=y egyenletrendszerben, melyekre az egyenletrendszer megoldható.

Világos, hogy az első esetben Gauss-eliminációval kell megoldani a feldatot, a második esetben azokat az y-okat kell behatárolni, amelyre az (M|y) kibővített együtthatómátrix rangja egyezik M rangjával.

Lineáris leképezés magtere és képtere

A ∈ Hom(V,U), akkor

$\mathrm{Ker}(\mathcal{A})=\{\mathbf{v}\in V\mid \mathcal{A}\mathbf{v}=\mathbf{0}\}$

$\mathrm{Im}(\mathcal{A})=\{\mathcal{A}\mathbf{v}\in U\mid \mathbf{v}\in V\}$

Ezekkel a fogalmakkal kapcsolatos a vektorterek dimenziótétele. Ha A ∈ Hom(V,U), akkor

$\mathrm{dim}\,\mathrm{Ker}(\mathcal{A})+\mathrm{dim}\,\mathrm{Im}(\mathcal{A})=\mathrm{dim}\,U$

Feladatok

1.

Alteret alkotnak-e?

R[X]-ben, a valósegyütthatós polinomok terében a
- { p | deg(p)=100 vagy p=0 }
- { p | deg(p) 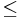$\leq$ 100 vagy p=0 }
- { p | p-nek van valós gyöke }
A valós számsorozatok terében a
- { s | s korlátos }
- { s | s konvergens }
- {s | s véges sok helyen nemnulla}
A valós függvények terében a
- { f | f periodikus }
- { f | f(1) > 0 }
- {f | f injektív }

2.

Mi az

$A=\begin{pmatrix} 1 & 2 & 3 & 4\\ 2 & 3 & 4 & 5 \\ 3 & 4 & 5 & 6 \end{pmatrix}$

képtere és magtere?

@@ 49. sor: / 49. sor: @@
 Ezekkel a fogalmakkal kapcsolatos a vektorterek dimenziótétele. Ha ''A'' &isin; Hom(''V'',''U''), akkor
-:<math>\mathrm{dim}\mathrm{Ker}(\mathcal{A})+\mathrm{dim}\mathrm{Im}(\mathcal{A})=\mathrm{dim}(U)</math>
+:<math>\mathrm{dim}\,\mathrm{Ker}(\mathcal{A})+\mathrm{dim}\,\mathrm{Im}(\mathcal{A})=\mathrm{dim}\,U</math>
 ==Feladatok==

Lineáris altér

A lap 2008. március 3., 22:58-kori változata

Tartalomjegyzék

Altér jellemzése

Példák

Triviális alterek

Generált altér

Mátrix magtere és képtere

Lineáris leképezés magtere és képtere

Feladatok

1.

2.

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök