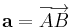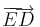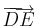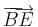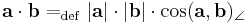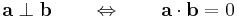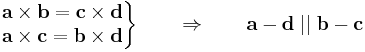Matematika A1 2024/1. hét

A MathWikiből

(Változatok közti eltérés)

A lap 2024. február 26., 17:43-kori változata

_{Matematika A1 2024}

Tartalomjegyzék

1 Vektorok
2 Vektorműveletek
3 Házi feladatok

Vektorok

Irányított egyenes szakaszok között definiálunk egy "egyenlőséget", lényegben azzal, hogy az egyenlő nagyságú, egymással párhuzamos, azonos irányítású irányított egyenes szakaszokat azonosnak vesszük. Ha összegyűjtjük az egy halmazba az összes egymással egyenlőnek tekintett irányított egyenes szakaszt, akkor ezt a halmazt vektornak, elemeit a vektor egy reprezentánsának nevezzük. Jelben: ha a vektor, akkor

$\mathbf{a}=\overrightarrow{AB}$

jelöli, hogy 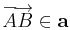$\overrightarrow{AB}\in \mathbf{a}$ .

Az a vektor hossza

|a|

nem más, mint mely bármely reprezentánsának hossza.

Nullvektor az aminek a hossza 0 (kezdőpontja és végpontja azonos).

Két vektor párhuzamos:

a || b

ha van egy-egy reprezentánsuk, amelyek egyenesei párhuzamosak egymással.

Két párhuzamos vektor azonos állású vagy irányítású vagy egyirányúak, jelben:

$\mathbf{a}\uparrow\uparrow\mathbf{b}$

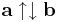
ha a reprezentánsaik azonos irányításúak; a 0 mindennel azonos irányú. Ha ezek a párhuzamos vektorok olyanok, hogy nem egyirányúak, akkor ennek jelölése:

$\mathbf{a}\uparrow\downarrow\mathbf{b}$

Tehát:

Definíció. a = b, akkor és csak akkor, ha

|a| = |b| és
a || b és
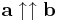
$\mathbf{a}\uparrow\uparrow\mathbf{b}$

Vektorműveletek

Összeadás

Az összeadást a geometriai tulajdonsága, azaz a paralelogramma szabály definiálja.

Legyen a és b két vektor és 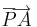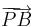$\overrightarrow{PA}$ , $\overrightarrow{PB}$ rendre a két vektor azonos kezdőpontból felmért reprezentánsa, legyen továbbá PACB paralelogramma (P-vel szemközt: C). Ekkor a + b vektor definíció szerint az a c vektor, melyet 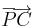$\overrightarrow{PC}$ reprezentál.

Az a ellentett vektora az a -a vektor, melyre |-a| = |a|, 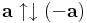$\mathbf{a}\uparrow\downarrow(-\mathbf{a})$ .

Kivonás: a - b =_def a + (-b)

Több vektor összeadása mehet úgy nevezett vektorfűzéssel, amikor az egyik végpontjából mérjük fel a következő vektort...

(A vektorösszeadás olyan tulajdonságú, mint a valós számok összeadása: kommutatív, asszociatív, 0 -t bármihez adva, amaz nem változik, ellentettjét a vektorhoz adva 0-t kapunk.) Tehát:

Az összeadás algebrai tulajdonságai

(a + b) + c = a + (b + c)

a + 0 = 0 + a = a

a + (-a) = (-a) + a = 0

a + b = b + a

Számmal való szorzás

Vektor számmal való szorzását a vektoregyenlőség esetei szerint definiáljuk.

Legyen a vektor, λ valós szám. Ekkor

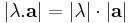$|\lambda.\mathbf{a}|=|\lambda|\cdot |\mathbf{a}|$ ,

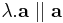$\lambda.\mathbf{a}\;||\;\mathbf{a}$ ,

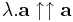$\lambda.\mathbf{a}\uparrow\uparrow\mathbf{a}$ , ha λ > 0 és 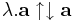$\lambda.\mathbf{a}\uparrow\downarrow\mathbf{a}$ , ha λ < 0

Geometriai tulajdonság

λa az a vektor λ-szorosára nyújtott vagy zsugorított verziója (nyuzsorítás). Ha λ<0, akkor az eredetihez képest az irányítása megfordul.

Algebrai tulajdonságok

(Széttagolja a valós és a vektorösszeget, felcserélhető a valós szorzással, az 1-gyel való szorzás azonos az identitással.)

λ.(μ'a) = (λμ).a

λ.(a + b) = λ.a + λ.b

(λ+μ).a = λ.a + μ.a

1.a = a

1. Feladat. ABCDEF egy szabályos hatszög. Fejezzük ki az a = 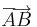$\overrightarrow{AB}$ és b = 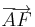$\overrightarrow{AF}$ vektorok összegével/számszorosával a

$\overrightarrow{ED}$

$\overrightarrow{DE}$

$\overrightarrow{AD}$

$\overrightarrow{BE}$

vektorokat!

Skaláris szorzás

Az a és b vektorok skaláris szorzata az

$\mathbf{a}\cdot\mathbf{b}=_{\mathrm{def}}|\mathbf{a}|\cdot|\mathbf{b}|\cdot\cos(\mathbf{a},\mathbf{b})_{\angle}$

szám.

(Széttagolja az összeget, felcserélhető a számmal való szorzással (mindkét változójában)).

e egységvektor, ha |e| = 1.

Geometriai tulajdonsága.

Ha e egységvektor, akkor v $\cdot$ e a v-nek az e egyenesére eső merőleges vetületének előjeles hossza.
a, b nem nullvektorok, akkor
$\mathbf{a}\;\bot\;\mathbf{b}\quad\quad\Leftrightarrow\quad\quad \mathbf{a}\cdot\mathbf{b}=0$

2. Feladat. Legyen ABCD egy téglalap, melynek AB oldala 5 egység, AD oldala 4 egység. Legyen a az 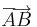$\overrightarrow{AB}$ irányú egységvektor, és b az 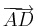$\overrightarrow{AD}$ irányú egységvektor. Legyen továbbá E az AD felezéspontja, G az AB B-hez közelebbi ötödölőpontja és az egyel beljebbi az F. Igazolja, hogy GE merőleges FC-re!

Vektoriális szorzás

Az a és b térvektorok vektoriális szorzata az a c = a × b vektor, melyre

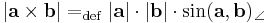
$|\mathbf{a}\times\mathbf{b}|=_{\mathrm{def}}|\mathbf{a}|\cdot|\mathbf{b}|\cdot\sin(\mathbf{a},\mathbf{b})_{\angle}$
merőleges az a és b által kifeszített síkra,
irányítása olyan, hogy (a, b, a × b) ilyen sorrendben jobbrendszert alkot, azaz a jobb kéz hüvelyk, mutató és középső ujját kifeszíthetjük "fájdalommentesen" úgy, hogy rendre a a, b, a × b vektorok irányát kapjuk.

Széttagolja az összeget, felcserélhető a számmal való szorzással, de nem asszociatív és nem kommutatív, bár antikommutatív, azaz a szorzat ellenkezőjébe megy át a két tényező felcserélésével kapott szorzat.

Geometriai tulajdonsága.

|a × b| az a és b által kifeszített paralelogramma területe.
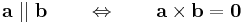
$\mathbf{a}\;||\;\mathbf{b}\quad\quad\Leftrightarrow\quad\quad \mathbf{a}\times\mathbf{b}=\mathbf{0}$

3. Feladat. Legyen ABC háromszög, S a súlypontja, F az AB felezéspontja. Határozzuk meg, hogy az ABC háromszög területének hanyadrésze az AFS háromszog területe.

vagy

Igazoljuk, hogy az egyenlőszárú háromszög magassága felezi az alapot!

4. Feladat. Igazoljuk, hogy

$\left.\begin{matrix} \mathbf{a}\times\mathbf{b}=\mathbf{c}\times\mathbf{d}\\ \mathbf{a}\times\mathbf{c}=\mathbf{b}\times\mathbf{d} \end{matrix}\right\}\quad\quad \Rightarrow\quad\quad \mathbf{a}-\mathbf{d}\;||\;\mathbf{b}-\mathbf{c}$

Házi feladatok

Igazolja, hogy az paralelogramma átlóinak felezőpontjai egybeesnek!
Igaz-e:
1. ha ab = 0, akkor a és b közül legalább az egyik nulla.
2. ha ab = ac, és a ≠ 0, akkor b = c
3. ha ab = ac, akkor vagy b - c || a, vagy b - c 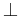$\bot$ a
Igaz-e:
1. ha a×b = 0, akkor a és b közül legalább az egyik nulla.
2. ha a×b = a×c, és a ≠ 0, akkor b = c
3. ha a + b + c = 0, akkor a×b = b×c = c×a
1. Igazolja a Thalész-tételt (azaz, hogy ha egy szakasz fölé, mint átmérő fölé kört rajzolunk, akkor a kör bármely (szakaszon kívüli) pontjából a szakasz két végpontja derékszög alatt látszik)!
2. Igazolja a koszinusztételt, azaz hogy az a,b,c oldalú háromszögben (γ a c-hez tartozó szög)
  $c^2=a^2 + b^2 -2ab\cos\gamma\,$

2. gyakorlat

@@ 66. sor: / 66. sor: @@
 &lambda;'''a''' az '''a''' vektor &lambda;-szorosára nyújtott vagy zsugorított verziója (nyuzsorítás). Ha  &lambda;<0, akkor az eredetihez képest az irányítása megfordul.
-===Algebrai tulajdonságok===
+====Algebrai tulajdonságok====
 (Széttagolja a valós és a vektorösszeget, felcserélhető a valós szorzással, az 1-gyel való szorzás azonos az identitással.)