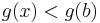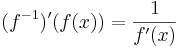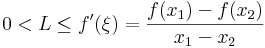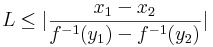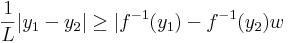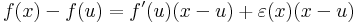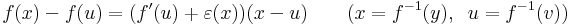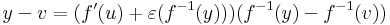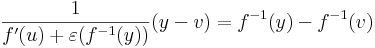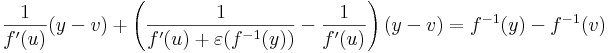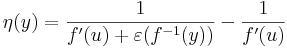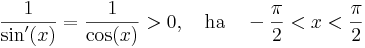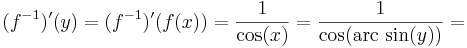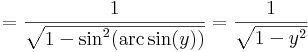Matematika A1a 2008/10. gyakorlat
Mozo (vitalap | szerkesztései) (→Lagrange-tétel) |
Mozo (vitalap | szerkesztései) (→Folytonos differenciálhatóság) |
||
| (egy szerkesztő 71 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
<sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub> | <sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub> | ||
| − | == | + | ==A derivált korlátosságának témaköre== |
| − | + | ===Egyenletes folytonosság=== | |
| − | + | ||
| − | + | A folytonosság lokális tulajdonság. Létezik azonban ennek a fogalomnak globális változata is. A jellegzetes különbségre a két folytonosság között, a következő kérdés mutat rá. Igaz-e, hogy a ''H'' halmazon folytonos ''f'' függvény kiterjeszthető úgy a ''H'' halmaz lezártjára olymódon, hogy a kiterjesztés is folytonos lesz? A válasz nem: az | |
| − | :<math> | + | :<math>f:(0,+\infty)\to \mathbf{R},\;x\mapsto \sin\frac{1}{x}</math> |
| − | + | függvénynek nincs folytonos kiterjeszése a [0,+∞) zárt halmazra, hisz a 0-ban nem létezik határértéke. | |
| − | + | ||
| − | + | ||
| − | + | Az egyenletesen folytonos függvények azonban ilyenek lesznek (alább egy példában belátjuk, hogy a fenti függvény valóban nem egyenletesen folytonos). | |
| − | :<math>\ | + | '''Definíció.''' Legyen ''f'' a valós számok egy részhalmazán értelmezett, valósba képező függvény és ''H'' ⊆ Dom(''f''). Azt mondjuk, hogy az ''f'' '''egyenletesen folytonos a H halmazon''', ha |
| + | :<math>(\forall\varepsilon>0)(\exists \delta>0)(\forall x,y\in H)(|x-y|<\delta\;\Rightarrow\;|f(x)-f(y)|< \varepsilon)</math> | ||
| − | + | Tehát az egyenletes folytonosság '''közös''' delta létezését állítja minden a halmazban lévő pontra, szemben a pontbéli folyonossággal, mely csak külön deltákat garantál mindenhol. | |
| − | Legyen ''f'': [''a'',''b''] <math>\to</math> '''R''' differenciálható | + | '''Példa.''' A négyzetgyök-függvény egyenletesen folytonos. |
| − | :<math>\frac{f(b)-f(a)}{b-a}=f'(\xi)\,</math> | + | |
| + | ''Elemi úton látjuk be.'' Egyfelől világos, hogy ha ε>0, akkor a δ = ε<sup>2</sup> olyan, hogy minden nemnegatív ''x''-re, ha ''x'' < δ, akkor | ||
| + | :<math>\sqrt{x}<\varepsilon\,</math> | ||
| + | Másrészt legyen ''x'', ''y'' > 0 és legyen ε>0. Ekkor a δ = ε<sup>2</sup> szintén alkalmas választás, mert: | ||
| + | :<math>|\sqrt{x}-\sqrt{y}|=\frac{|x-y|}{\sqrt{x}+\sqrt{y}}=\sqrt{|x-y|}\frac{\sqrt{|x-y|}}{\sqrt{x}+\sqrt{y}}\leq\sqrt{|x-y|}\frac{\sqrt{x+y}}{\sqrt{x}+\sqrt{y}}\leq</math> | ||
| + | :<math>\leq\sqrt{|x-y|}\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}+\sqrt{y}}=\sqrt{|x-y|}<\sqrt{\delta}=\sqrt{\varepsilon^2}=\varepsilon</math> | ||
| + | Tehát bármely ε-hoz ''közös'' δ található minden ponthoz. | ||
| + | |||
| + | '''Nem egyenletes folytonosság jellemzése.''' Ha azt szeretnénk definíció szerint belátni, hogy egy függvény nem egyenletesen folytonos egy halmazon, akkor a folytonossághoz hasonló módon a sorozatokkal történő jellemzés eszközéhez szoktunk folyamodni. Először is a definíció tagadását kell felírnunk, ebből fogjuk a sorozatokkal jellemezni a nem-egyenletes folytonosságot. | ||
| + | |||
| + | ''f'' nem egyenletesen folytonos a ''H'' halmazon, ha | ||
| + | |||
| + | :<math>(\exists \varepsilon>0)(\forall \delta>0)(\exists x,y \in H)(|x-y|< \delta,\;\;\mathrm{de}\;\;|f(x)-f(y)|\geq\varepsilon)</math> | ||
| + | |||
| + | Itt δ helyett írhatjuk az (1/n) sorozatot, hiszen, ha minden ''n''-re igaz a kijelentés a δ=1/n-re, akkor minden δ-ra is igaz: | ||
| + | |||
| + | :<math>(\exists \varepsilon>0)(\forall n\in\mathbf{Z}^+)(\exists x_n,y_n \in H)(|x_n-y_n|< \frac{1}{n},\;\;\mathrm{de}\;\;|f(x_n)-f(y_n)|\geq\varepsilon)</math> | ||
| + | |||
| + | A következő példák erre vonatkoznak: | ||
| + | |||
| + | '''Példa.''' A reciprok a pozitív számok halmazán nem egyenletesen folytonos. | ||
| + | |||
| + | ''Ugyanis.'' Például az ε=1 esetén minden δ=1/n-re meg kell adnunk olyan <math>x_n</math> és <math>y_n</math> pozitív számokat, hogy ''bár'' <math>|x_n-y_n|<1/n</math>, ''de'' <math>|(1/x_n)-(1/y_n)|\geq 1</math> legyen. Márpedig | ||
| + | :<math>x_n=\frac{1}{n}</math> és <math> y_n=\frac{1}{n+1}\,</math> | ||
| + | ilyen. A különbségük a 0-hoz tart, a reciprok-különbségük viszont 1. | ||
| + | |||
| + | '''Példa.''' Legyen | ||
| + | :<math>f(x)=\sin(1/x)\,</math>, | ||
| + | és vizsgáljuk meg, hogy ez egyenletesen folytonos-e a (0,1) nyílt intervallumon. | ||
| + | |||
| + | ''Mo.'' Bár f folytonos a (0,1)-en, de a (0,1) nem zárt, azaz a Heine-tétel (lásd alább) nem alkalmazható. Hasonlóképpen a függvény deriváltja nem korlátos, ezért a később említendő kritérium sem alkalmazható. Gyanítható, hogy a függvény nem egyenletesen folytonos. | ||
| + | |||
| + | Legyen ε = 1. Kiválasztjuk f nullhelyeit az egyik, a maximumhelyeit a másik sorozatnak, mert ezek függvényértékeinek különbsége biztos, hogy nem tart a nullához: | ||
| + | :<math>x_n=\frac{1}{2n\pi}</math> | ||
| + | :<math>y_n=\frac{1}{2n\pi+\frac{\pi}{2}}</math> | ||
| + | Ekkor | ||
| + | :<math>x_n-y_n=\frac{1}{2n\pi}-\frac{1}{2n\pi+\frac{\pi}{2}}=\frac{\frac{\pi}{2}}{2n\pi(2n\pi+\frac{\pi}{2})}<\frac{\frac{\pi}{2}}{4n^2\pi^2}=\frac{1}{8n^2\pi}<\frac{1}{n}</math> | ||
| + | de a függvényértékek különbsége: | ||
| + | :<math>|\sin(x_n)-\sin(y_n)|=|\sin(2n\pi)-\sin(2n\pi+\pi/2)|=|0-1|=1\geq\varepsilon</math> | ||
| + | azaz nagyobb egyenlő a megadott epszilonnál. | ||
| + | |||
| + | ===Heine tétele=== | ||
| + | |||
| + | '''Tétel''' -- ''Heine tétele'' -- Zárt és korlátos intervallumon értelmezett folytonos függvény egyenletesen folytonos. | ||
| + | |||
| + | '''Példa.''' Igazoljuk, hogy a | ||
| + | :<math>g(x)=x\sin(1/x)\,</math> | ||
| + | függvény egyenletesen folytonos a (0,1) intervallumon. | ||
| + | |||
| + | ''Mo.'' g-nek van folytonos kiterjesztése a [0,1] zárt korlátos intervallumra, mert egyfelől 1-ben értelmezhető folytonos módon a fenti formulával, másfelől 0-ban korlátos szor nullához tartó alakú, azaz a határértéke nulla. Legyen | ||
| + | :<math>h(x)=\begin{cases}x\sin(1/x),\;\;x\ne 0\\0, \;\;x=0\end{cases}</math> | ||
| + | h folytonos a zárt [0,1]-en, így Heine tétele miatt egyenletesen folytonos. De tudjuk, hogy egyenletesen folytonos függvény minden leszűkítése is egyenletesen folytonos, azaz h leszűkítése a g is egyenletesen folytonos. Ez az előbb említett, a leszűkítésre vonatkozó állítás azért igaz, mert ha van közös delta egy bővebb halmazon, akkor nyilván ugyanez a delta jó lesz a szűkebb halmazon is. | ||
| + | |||
| + | ===Lipschitz-tulajdonság=== | ||
| + | |||
| + | Jellegzetes folytonosságtípus a Lipschitz-folytonosság. | ||
| + | |||
| + | '''Definíció.''' A f:'''R''' ⊇ ''A'' <math>\to</math> '''R''' függvény Lipschitz-tulajdonságú, ha létezik olyan ''L'' > 0 szám, hogy minden x,y ∈ ''A''-ra: | ||
| + | :<math>|f(x)-f(y)|\leq L|x-y|</math> | ||
| + | |||
| + | Világos, hogy ekkor ''f'' egyenletesen folytonos ''A''-n, ugyanis legyen ε > 0. Ekkor a δ = ε/L olyan, hogy ha |x-y| < δ, akkor | ||
| + | :<math>|f(x)-f(y)|\leq L|x-y|<L\delta=\varepsilon\,</math> | ||
| + | Fordítva már nem igaz. A gyökfüggvény egyenletesen folytonos, de nem Lipschitz-tulajdonságú, ugyanis x=1/n, y=1/(n+1)-gyel: | ||
| + | :<math>\sqrt{\frac{1}{n})}-\sqrt{\frac{1}{n+1}}=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n(n+1}}=\frac{1}{(\sqrt{n}+\sqrt{n+1})\sqrt{n(n+1)}}=</math> | ||
| + | :<math>=\frac{\sqrt{n(n+1)}}{(\sqrt{n}+\sqrt{n+1})}\frac{1}{n(n+1)}\geq_{n>N}n\cdot(\frac{1}{n}-\frac{1}{n+1})</math> | ||
| + | |||
| + | Intervallumon értelmezett differenciálható függvény pontosan akkor Lipschtz-tulajdonságú, ha a deriváltja korlátos. | ||
| + | |||
| + | Ugyanis, 1) ha korlátos a derivált, akkor a Lagrange-tétellel találunk L-et. 2) ha lipschiztes, akkor minden különbségi hányadosnak ugyanaz a korlátja, így korlátos a derivált. | ||
| + | |||
| + | ===Korlátos derivált=== | ||
| + | Ha az ''f'' intervallumon értelmezett differenciálható függvény korlátos deriválttal rendelkezik, akkor a Lagrange-féle középértéktétel miatt ''f'' egyenletesen folytonos, sőt Lischitz-tulajdonsgú az értelmezési tartományán. Ugyanis legyen ''K'' olyan pozitív szám, hogy minden x ∈ Dom(''f'')-re: | ||
| + | :<math>|f'(x)| \leq K \,</math> | ||
| + | Ha ε > 0 és δ:=ε/''K'', akkor minden x,y ∈ Dom(''f'')-re, ha |x-y| < δ, létezik ξ az x és az y között, hogy azzal: | ||
| + | :<math>|f(x)-f(y)|= |f'(\xi)|\cdot|x-y|< K\cdot \delta=\varepsilon</math> | ||
| + | |||
| + | '''Példa.''' Az | ||
| + | :<math>f(x)=\frac{1}{x}\,</math> | ||
| + | egyenletesen folytonos az [1,+∞) halmazon. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Ugyanis,'' itt korlátos a deriváltja: | ||
| + | :<math>\left(\frac{1}{x}\right)'=-\frac{1}{x^2}\,</math> | ||
| + | Ezért ha x ∈ [1,+∞), akkor | ||
| + | :<math>\left| -\frac{1}{x^2}\right|=\frac{1}{x^2}\leq 1</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''Példa.''' A mindenhol értelmezett | ||
| + | :<math>f(x)=\cos\sqrt[3]{x}\,</math> | ||
| + | függvény egyenletesen folytonos. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Ugyanis,'' a [-1,1] zárton a Heine-tétel miatt egyenletesen folytonos, azon kívül pedig | ||
| + | :<math>|f'(x)|=|\sin(\sqrt[3]{x})\cdot\frac{1}{3\sqrt[3]{x^2}}|\leq 1\cdot \frac{1}{3}=\frac{1}{3}</math> | ||
| + | |||
| + | == Folytonos differenciálhatóság== | ||
| + | |||
| + | '''Tétel. ''' -- Zárt intervallumon differenciálható függvény deriválfüggvénynek, nem lehet megszüntethető szakadása. | ||
| + | |||
| + | ''Ugyanis.'' Legyen f:[a,b] <math>\to</math> '''R''' diff.-ható és tegyük fel, hogy létezik a | ||
| + | :<math>\lim\limits_{x\to a}f'(x)\,</math> | ||
| + | és véges. Ekkor belátjuk, hogy ez a derivált a-beli helyettesítési értéke. Kiszámítjuk különbségi hányados határértéktét! Vegyük az x<sub>n</sub> = a + 1/n sorozatot (ill ennek [a,b]-beli részét). Minden [a,a+1/n] intervallumra felírhatjuk a Lagrange-tételt: | ||
| + | : <math>\frac{f(x_n)-f(a)}{x_n-a}=f'(\xi_n)</math> | ||
| + | Ekkor a különbségi hányados függvényértékek sorozata egyenlő lesz a derivált egy függvényértéksorozatával, melyek így ugyanahhoz tartanak. De ez csak az f'(a) és a lim<sub>u</sub>f' számok lehetnek, amik így egyenlők. | ||
| + | |||
| + | Ne keressünk tehát sem ugrást, sem megszüntethető szakadást a derivátlfüggvényen. Ellenben lehet korlátos másodfajú és a végtelen másodfajú szakadása. | ||
| + | |||
| + | '''6. Feladat.''' Határozzuk meg, hogy az alábbi függvények folytonosan differencálhatóak-e? | ||
| + | |||
| + | # <math>f(x)=\left\{\begin{matrix}x^2\sin\left(\cfrac{1}{x}\right)& \mathrm{ha} & x\ne 0\\ | ||
| + | 0 &\mathrm{ha} & x=0 | ||
| + | \end{matrix}\right.</math> | ||
| + | # <math>f(x)=\left\{\begin{matrix}x^2\sin\left(\cfrac{1}{x^2}\right)& \mathrm{ha} & x\ne 0\\ | ||
| + | 0 &\mathrm{ha} & x=0 | ||
| + | \end{matrix}\right.</math> | ||
| + | # <math>f(x)=\left\{\begin{matrix}\sin(x^2)\frac{e^x-1}{x}& \mathrm{ha} & x\ne 0\\ | ||
| + | 0 &\mathrm{ha} & x=0 | ||
| + | \end{matrix}\right.</math> | ||
| + | |||
| + | ''Megoldás.'' Mindegyiknél a metódus az, hogy (A) Meghatározzuk a deriváltfüggvény határértékét , (B) meghatározzuk a pontbeli deriváltat (C) Megnézzük, hogy egyenlők-e? Ha (A)-ban nincs határérték, akkor abból már kövevetkezik, hogy nem folyt. diff a függvény. | ||
| + | |||
| + | 1. | ||
| + | :<math> \left(x^2\sin\left(\cfrac{1}{x}\right)\right)'=2x\sin\left(\cfrac{1}{x}\right)+x^2\cos\left(\cfrac{1}{x}\right)\frac{-1}{x^2}=2x\sin\left(\cfrac{1}{x}\right)-\cos\left(\cfrac{1}{x}\right)</math> | ||
| + | nem folyt diff a 0-ban, mert nincs lim<sub>0</sub> f', mert a második tag határértéke nem létezik (bár korlátos). | ||
| + | |||
| + | 2. | ||
| + | :<math> \left(x^2\sin\left(\cfrac{1}{x^2}\right)\right)'=2x\sin\left(\cfrac{1}{x^2}\right)+x^2\cos\left(\cfrac{1}{x^2}\right)\frac{-2}{x^3}=2x\sin\left(\cfrac{1}{x^2}\right)-\frac{2}{x}\cos\left(\cfrac{1}{x}\right)</math> | ||
| + | nwm folyt diff a 0-ban, mert nincs lim<sub>0</sub> f', mert a második tag határértéke nem létezik és nem is korlátos. | ||
| + | |||
| + | 3. | ||
| + | :<math>f'(x)=\cos(x^2)\cdot\frac{e^x-1}{x}+\sin(x^2)\cdot \frac{e^x(x-1)}{x^2}\to 0</math> | ||
| + | Már csak a pontbeli deriváltat kell kiszámítani. Ez is 0. | ||
| + | |||
| + | A fenti tételen kívül több is igaz. | ||
| + | |||
| + | '''Állítás.''' Ha ''f'':[a,b] <math>\to</math> '''R''' folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor ''f''-nek ''létezik'' a deriváltja a-ban (és a deriváltja a fent említett tétel miatt a lim<sub>a</sub> f' szám. | ||
| + | |||
| + | ''Bizonyítás.'' A későbbiekben igazolandó erős L'Hospital-tétel következménye. Tekintsük a különbségi hányados függvényt, legyen a L'H-beli "f" az f(x)-f(a), az x-a a g. Ekkor | ||
| + | :<math>\lim\limits_{x\to a}\frac{f(x)-f(a)}{x-a}=\lim\limits_{x\to a}\frac{f'(x)}{1}=\lim\limits_{x\to a}f'(x)</math> | ||
| + | azaz ''létezik'' a pontbeli derivált és ez a derivált határértéke. | ||
| + | |||
| + | '''Kérdés:''' hol használtuk fel, hogy az f függvény folytonos? | ||
| + | |||
| + | '''Tétel.''' -- Darboux-tétel -- Az ''f'':[a,b] <math>\to</math> '''R''' differenciálható függvény deriváltfüggvénye Darboux-tulajdonságú (azaz minden ilyen függvény két függvényértéke között minden értéket fölvesz). | ||
| + | |||
| + | ''Ugyanis, '' Legyen f'(a)<m<f'(b) és igazoljuk, hogy létezik ξ ∈ (a,b), hogy f'(ξ) = ''m''. Vegyük a Lagrange-tételhez hasonlóan a | ||
| + | :<math>g(x)=f(x)-mx\, </math> | ||
| + | függvényt. Megállapíthatjuk, hogy tetszőleges ''x'' ∈ (a,b)-re | ||
| + | :<math>g'(x)=0 \quad\quad \Leftrightarrow \quad\quad f'(x)=m</math> | ||
| + | ha tehát keresünk ''g''-hez stacionárius pontot (a,b)-n, akkor megtaláltuk ξ-t. Ilyet a Weierstrass-tétellel kereshetünk. g folytonos, így van maximuma és minimuma. Kell, hogy legyen belül is, ugyanis, ha csak kívül venné fel a szélsőértékeit, akkor a következő történne. g'(a) < 0, így a-ban g lokálisan csökken, hiszen ekkor van olyan kis intervallum, ahol az a-beli különbségihányados függvény negatív, azaz | ||
| + | :<math>g(x)< g(a)\,</math> | ||
| + | ugyanekkor egy kis környzetben b-körül a függvény szintén lokálisan, hiszen | ||
| + | :<math>\frac{g(x)-g(b)}{x-b}>0\quad\quad(x\in(b-\delta,b])</math> | ||
| + | és így | ||
| + | :<math>g(x)< g(b)\,</math> | ||
| + | Sem a-ban, sem b-ben ezek szerint nem lehet a ξ minimum, így annak belül kell lennie. Ekkor viszont alkalmazható a Fermat-tétel, mellyel: | ||
| + | :<math>g'(\xi)=0\,</math>, azaz <math>f'(\xi)=m\,</math> | ||
| + | |||
| + | '''Feladat.''' Igaz-e? | ||
| + | # '''R''' <math>\to</math> '''R''' differenciálható függvény ''deriváltfüggvénye'' minden zárt és korlátos intervallumon felveszi minimumát és maximumát. | ||
| + | # Ha az '''R''' <math>\to</math> '''R''' differenciálható függvény ''deriváltfüggvénye'' negatív és pozitív értékeket is felvesz, akkor van a driváltnak zérushelye. | ||
| + | # '''R''' <math>\to</math> '''R''' differenciálható függvény ''deriváltfüggvénye'' korlátos, akkor létezik olyan L szám, hogy minden x,y-ra: |f(x)-f(y)| < L|x-y|. | ||
| + | # A deriválható függvények egyenletesen folytonosak. | ||
| + | # Korlátos és zárt intervallumon differenciálható függvények egyenletesen folytonos. | ||
| + | # A korlátos deriválttal rendelkező függvények egyenletesen folytonosak. | ||
| + | |||
| + | ==Inverzfüggvénytétel '''R'''-re== | ||
| + | |||
| + | <!--'''Inverzfüggvény deriváltja.''' Ha az ''f'' invertálható függvény differenciálható ''u''-ban, ''f'' <sup>-1</sup> folytonos ''u''-ban és f'(u) ≠ 0, akkor az inverz is differenciálható ''u''-ban és | ||
| + | :<math>(f^{-1})'(f(u))=\frac{1}{f'(u)}\,</math> | ||
| + | |||
| + | ''Biz.'' | ||
| + | :<math>f(x)-f(u)=f'(u)(x-u)+\varepsilon(x)(x-u)\,</math> | ||
| + | :<math>f(x)-f(u)=(f'(u)+\varepsilon(x))(x-u)\quad\quad(x=f^{-1}(y),\;\;u=f^{-1}(v))</math> | ||
| + | :<math>y-v=(f'(u)+\varepsilon(f^{-1}(y)))(f^{-1}(y)-f^{-1}(v))\,</math> | ||
| + | :<math>\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}(y-v)=f^{-1}(y)-f^{-1}(v)\,</math> | ||
| + | :<math>\frac{1}{f'(u)}(y-v)+\left(\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}-\frac{1}{f'(u)}\right)(y-v)=f^{-1}(y)-f^{-1}(v)\,</math> | ||
| + | Itt az | ||
| + | :<math>\eta(y)=\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}-\frac{1}{f'(u)}\,</math> | ||
| + | függvény akkor lesz folytonos és ''v''-ben eltűnő, ha maga f<sup>-1</sup> is folytonos ''v''-ben. | ||
| + | |||
| + | '''Megjegyzás.''' A tételi állításban az inverz folytonossági feltétele csak olyan esetben jelent megszorítást, amikor a függvény nem intervallumon értelmezett szigorúan monoton függvény. Példa olyan invertálható függvényre, melynek deriváltja nem nulla egy adott pontban, de inverze a képpontban nem folytonos: | ||
| + | :<math>\mathrm{Dom}\,f=\mathbf{R}\setminus\left\{\frac{1}{n}\right\}_{n\in \mathbf{Z}^+}</math> | ||
| + | :<math>f(x)=\left\{\begin{matrix}x, & \mathrm{ha} & x\not\in \mathbf{Z}^+\\ | ||
| + | \frac{1}{x}, & \mathrm{ha} & x= n\in \mathbf{Z}^+ | ||
| + | \end{matrix}\right.</math> | ||
| + | |||
| + | ''f'' ekkor a 0-ban deriválható és ''f'' '(0)=1, invertálható, mert '''R''' \ (1/'''Z'''<sup>+</sup>) \ '''Z'''<sup>+</sup>-n az identitás és az '''Z'''<sup>+</sup>-n pedig az 1/id, mely értékei vétetnek fel az '''R''' \ (1/'''Z'''<sup>+</sup>)- halmaz képeiként. Viszont így ''f''<sup>-1</sup> nem korlátos 0-ban, azaz nem folytonos, így nem is differenciálható. | ||
| + | |||
| + | ''Állítás.'' Intervallumon értelmezett szigorúan monoton függvény inverze folytonos (tehát ezesetben még akkor is folytonos az inverz, ha a függvénynek magának ugrása van). | ||
| + | |||
| + | Erre a meglepő eredményre egy illusztráló példát adunk. | ||
| + | |||
| + | ''Példa.'' Folytonosan invertálható-e az alábbi függvény? Indokoljuk a fenti tétel nélkül! | ||
| + | :<math>f(x)=\left\{\begin{matrix} | ||
| + | -x^2-1, & \mathrm{ha} & x<0\\ | ||
| + | 0, & \mathrm{ha} & x= 0\\ | ||
| + | x^2+1, & \mathrm{ha} & x>0 | ||
| + | \end{matrix}\right.</math> | ||
| + | ''Megoldás.'' Persze, hisz a negatívokon invertálható és csak negatív értéket vesz fel. A pozitívokon szintén és szintén csak pozitív értékeket vesz fel. A 0-beli érték az előző képhatlmazokon kívül esik (a 0). Az inverz: | ||
| + | :<math>\mathrm{Dom}\,f^{-1}=(-\infty,-1)\cup\{0\}\cup(1,+\infty)</math> | ||
| + | :<math>f^{-1}(y)=\left\{\begin{matrix} | ||
| + | -\sqrt{-y-1}, & \mathrm{ha} & y<-1\\ | ||
| + | 0, & \mathrm{ha} & y= 0\\ | ||
| + | \sqrt{y-1}, & \mathrm{ha} & y>1 | ||
| + | \end{matrix}\right.</math> | ||
| + | Ez a függvény mindenütt folytonos, mert a gyök az, és a 0-ban izolált pontja van, ahol a függvények triviálisan folytonosak. --> | ||
| + | |||
| + | '''Tétel''' -- Globális inverzfüggvény-tétel -- Ha ''f'': <math>I</math> <math>\to</math> '''R''' függvény folytonosan differenciálható és f' sehol se nulla, akkor | ||
| + | # ''f'' invertálható | ||
| + | # ''f'' inverze folytonos (''f'' homeomorfizmus) | ||
| + | # ''f'' inverze deriválható (''f'' diffeomorfizmus) | ||
| + | # minden x ∈ I-re | ||
| + | :<math>(f^{-1})'(f(x))=\frac{1}{f'(x)}\,</math> | ||
| + | |||
| + | ''Megjegyzés.'' Részeletesebb indoklás azt is kimutatja, hogy a derivált folytonossága nem szükséges (bár nem árt :). | ||
| + | |||
| + | ''Bizonyítás.'' 1) A derivált mindenhol azonos előjelű, ellenkező esetben lenne két hely, ahol különböző, de a Darboux-tétel miatt akkor lenne zérushelye is a deriváltnak, ami ellentmond a feltételeknek. Tehát ''f'' szigorúan monoton, így invertálható. | ||
| + | |||
| + | 2) Minden ''a'' ∈ I pontban a derivált nem nulla és folytonos, így létezik olyan környzete, melyben a derivált mindenhol egy L pozitív számál nagyobb. Ezért a Lagrange-tétel miatt a környzet bármely két <math>x_1</math>, <math>x_2</math> pontjára: | ||
| + | :<math>0<L\leq f'(\xi)=\frac{f(x_1)-f(x_2)}{x_1-x_2}</math> | ||
| + | Emiatt az x=f<sup>-1</sup>(y) áttéréssel: | ||
| + | :<math>L\leq |\frac{x_1-x_2}{f^{-1}(y_1)-f^{-1}(y_2)}|\,</math> | ||
| + | azaz | ||
| + | :<math>\frac{1}{L}|y_1-y_2|\geq |f^{-1}(y_1)-f^{-1}(y_2)w\,</math> | ||
| + | azaz az inverz lipschitzes a környzetben, azaz a pontban folytonos. | ||
| + | 3) 4) ezt egyszerre igazoljuk. Az ''u''-beli diffhatóság miatt: | ||
| + | :<math>f(x)-f(u)=f'(u)(x-u)+\varepsilon(x)(x-u)\,</math> | ||
| + | :<math>f(x)-f(u)=(f'(u)+\varepsilon(x))(x-u)\quad\quad(x=f^{-1}(y),\;\;u=f^{-1}(v))</math> | ||
| + | :<math>y-v=(f'(u)+\varepsilon(f^{-1}(y)))(f^{-1}(y)-f^{-1}(v))\,</math> | ||
| + | :<math>\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}(y-v)=f^{-1}(y)-f^{-1}(v)\,</math> | ||
| + | :<math>\frac{1}{f'(u)}(y-v)+\left(\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}-\frac{1}{f'(u)}\right)(y-v)=f^{-1}(y)-f^{-1}(v)\,</math> | ||
| + | Itt az | ||
| + | :<math>\eta(y)=\frac{1}{f'(u)+\varepsilon(f^{-1}(y))}-\frac{1}{f'(u)}\,</math> | ||
| + | függvény akkor lesz folytonos és ''v''-ben eltűnő, ha maga f<sup>-1</sup> is folytonos ''v''-ben. | ||
| + | |||
| + | |||
| + | '''Példa.''' Igazoljuk, hogy létezik a sin inverze a [-π/2,π/2]-n és az inverz folytonos a [-1,1]-en (ez az arcsin) ezen kívül az inverz deriválható a belső pontokban! | ||
| + | |||
| + | ''Ugyanis.'' [-π/2,π/2]-n a sin szigorúan monoton nő és inverz képe [-1,1]. Emiatt ez folytonos is és az inverzfüggvény-tétel miatt a nyílton differenciálható, ugyanis | ||
| + | :<math>\frac{1}{\sin'(x)}=\frac{1}{\cos(x)}>0,\quad \mathrm{ha}\quad -\frac{\pi}{2}<x<\frac{\pi}{2}</math> | ||
| + | az inverze: | ||
| + | :<math>(f^{-1})'(y)=(f^{-1})'(f(x))=\frac{1}{\cos(x)}=\frac{1}{\cos(\mathrm{arc\,\sin}(y))}=</math> | ||
| + | ::<math>=\frac{1}{\sqrt{1-\sin^2(\mathrm{arc\,sin}(y))}}=\frac{1}{\sqrt{1-y^2}}</math> | ||
| + | |||
| + | <!-- | ||
| + | ==Paraméteres görbe és Cauchy-féle középértéktétel== | ||
| + | |||
| + | Tegyük fel, hogy adva van az aritmetikai síkon ('''R'''<sup>2</sup>) egy | ||
| + | |||
| + | :<math>p:\,[a,b]\to \mathbf{R}^2;\;t\mapsto\left\{\begin{matrix}g(t)\\ f(t)\end{matrix}\right.</math> | ||
| + | görbe paraméteres alakban úgy, hogy g és f differenciálható függvények és g '''deriváltja sehol sem nulla'''. | ||
| + | |||
| + | Ekkor a globális inverzfüggvény-tételből következőleg a g szigorúan monoton, inverze differenciálható és kifejezhető x=g(t)-ből a t: | ||
| + | :<math>t=g^{-1}(x),\quad x\in [c,d]</math> | ||
| + | ahol [c,d] a g értékkészélete. | ||
| + | |||
| + | Ezzel a görbe implicit módon is megadható lesz, mint az | ||
| + | |||
| + | <math>F:[c,d] \to [a,b];\,x\mapsto f(g^{-1}(x))</math> | ||
| + | |||
| + | függvény grafikonja. Erre az F függvényre és a g(a), g(b) pontokra alkalmazva a Lagrange-tételt, létezik az (a,b) nyílton olyan ξ, hogy | ||
| + | :<math>\frac{F(g(b))-F(g(a))}{g(b)-g(a)}=\frac{f(b)-f(a)}{g(a)-g(b)}=F'(\xi)=f'(\xi)\cdot\frac{1}{g'(\xi)}=\frac{f'}{g'}(\xi)\,</math> | ||
| + | amit Cauchy-féle középértékételnek nevezünk. | ||
| + | |||
| + | Ebből következtethetünk az erős L'Hospital-szabály első deriválttas alakjára:--> | ||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A1]] | [[Kategória:Matematika A1]] | ||
A lap jelenlegi, 2014. november 26., 07:38-kori változata
Tartalomjegyzék |
A derivált korlátosságának témaköre
Egyenletes folytonosság
A folytonosság lokális tulajdonság. Létezik azonban ennek a fogalomnak globális változata is. A jellegzetes különbségre a két folytonosság között, a következő kérdés mutat rá. Igaz-e, hogy a H halmazon folytonos f függvény kiterjeszthető úgy a H halmaz lezártjára olymódon, hogy a kiterjesztés is folytonos lesz? A válasz nem: az
függvénynek nincs folytonos kiterjeszése a [0,+∞) zárt halmazra, hisz a 0-ban nem létezik határértéke.
Az egyenletesen folytonos függvények azonban ilyenek lesznek (alább egy példában belátjuk, hogy a fenti függvény valóban nem egyenletesen folytonos).
Definíció. Legyen f a valós számok egy részhalmazán értelmezett, valósba képező függvény és H ⊆ Dom(f). Azt mondjuk, hogy az f egyenletesen folytonos a H halmazon, ha
Tehát az egyenletes folytonosság közös delta létezését állítja minden a halmazban lévő pontra, szemben a pontbéli folyonossággal, mely csak külön deltákat garantál mindenhol.
Példa. A négyzetgyök-függvény egyenletesen folytonos.
Elemi úton látjuk be. Egyfelől világos, hogy ha ε>0, akkor a δ = ε2 olyan, hogy minden nemnegatív x-re, ha x < δ, akkor
Másrészt legyen x, y > 0 és legyen ε>0. Ekkor a δ = ε2 szintén alkalmas választás, mert:
Tehát bármely ε-hoz közös δ található minden ponthoz.
Nem egyenletes folytonosság jellemzése. Ha azt szeretnénk definíció szerint belátni, hogy egy függvény nem egyenletesen folytonos egy halmazon, akkor a folytonossághoz hasonló módon a sorozatokkal történő jellemzés eszközéhez szoktunk folyamodni. Először is a definíció tagadását kell felírnunk, ebből fogjuk a sorozatokkal jellemezni a nem-egyenletes folytonosságot.
f nem egyenletesen folytonos a H halmazon, ha
Itt δ helyett írhatjuk az (1/n) sorozatot, hiszen, ha minden n-re igaz a kijelentés a δ=1/n-re, akkor minden δ-ra is igaz:
A következő példák erre vonatkoznak:
Példa. A reciprok a pozitív számok halmazán nem egyenletesen folytonos.
Ugyanis. Például az ε=1 esetén minden δ=1/n-re meg kell adnunk olyan xn és yn pozitív számokat, hogy bár | xn − yn | < 1 / n, de 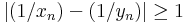 legyen. Márpedig
legyen. Márpedig
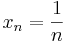 és
és 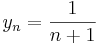
ilyen. A különbségük a 0-hoz tart, a reciprok-különbségük viszont 1.
Példa. Legyen
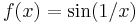 ,
,
és vizsgáljuk meg, hogy ez egyenletesen folytonos-e a (0,1) nyílt intervallumon.
Mo. Bár f folytonos a (0,1)-en, de a (0,1) nem zárt, azaz a Heine-tétel (lásd alább) nem alkalmazható. Hasonlóképpen a függvény deriváltja nem korlátos, ezért a később említendő kritérium sem alkalmazható. Gyanítható, hogy a függvény nem egyenletesen folytonos.
Legyen ε = 1. Kiválasztjuk f nullhelyeit az egyik, a maximumhelyeit a másik sorozatnak, mert ezek függvényértékeinek különbsége biztos, hogy nem tart a nullához:
Ekkor
de a függvényértékek különbsége:
azaz nagyobb egyenlő a megadott epszilonnál.
Heine tétele
Tétel -- Heine tétele -- Zárt és korlátos intervallumon értelmezett folytonos függvény egyenletesen folytonos.
Példa. Igazoljuk, hogy a
függvény egyenletesen folytonos a (0,1) intervallumon.
Mo. g-nek van folytonos kiterjesztése a [0,1] zárt korlátos intervallumra, mert egyfelől 1-ben értelmezhető folytonos módon a fenti formulával, másfelől 0-ban korlátos szor nullához tartó alakú, azaz a határértéke nulla. Legyen
h folytonos a zárt [0,1]-en, így Heine tétele miatt egyenletesen folytonos. De tudjuk, hogy egyenletesen folytonos függvény minden leszűkítése is egyenletesen folytonos, azaz h leszűkítése a g is egyenletesen folytonos. Ez az előbb említett, a leszűkítésre vonatkozó állítás azért igaz, mert ha van közös delta egy bővebb halmazon, akkor nyilván ugyanez a delta jó lesz a szűkebb halmazon is.
Lipschitz-tulajdonság
Jellegzetes folytonosságtípus a Lipschitz-folytonosság.
Definíció. A f:R ⊇ A  R függvény Lipschitz-tulajdonságú, ha létezik olyan L > 0 szám, hogy minden x,y ∈ A-ra:
R függvény Lipschitz-tulajdonságú, ha létezik olyan L > 0 szám, hogy minden x,y ∈ A-ra:
Világos, hogy ekkor f egyenletesen folytonos A-n, ugyanis legyen ε > 0. Ekkor a δ = ε/L olyan, hogy ha |x-y| < δ, akkor
Fordítva már nem igaz. A gyökfüggvény egyenletesen folytonos, de nem Lipschitz-tulajdonságú, ugyanis x=1/n, y=1/(n+1)-gyel:
Intervallumon értelmezett differenciálható függvény pontosan akkor Lipschtz-tulajdonságú, ha a deriváltja korlátos.
Ugyanis, 1) ha korlátos a derivált, akkor a Lagrange-tétellel találunk L-et. 2) ha lipschiztes, akkor minden különbségi hányadosnak ugyanaz a korlátja, így korlátos a derivált.
Korlátos derivált
Ha az f intervallumon értelmezett differenciálható függvény korlátos deriválttal rendelkezik, akkor a Lagrange-féle középértéktétel miatt f egyenletesen folytonos, sőt Lischitz-tulajdonsgú az értelmezési tartományán. Ugyanis legyen K olyan pozitív szám, hogy minden x ∈ Dom(f)-re:
Ha ε > 0 és δ:=ε/K, akkor minden x,y ∈ Dom(f)-re, ha |x-y| < δ, létezik ξ az x és az y között, hogy azzal:
Példa. Az
egyenletesen folytonos az [1,+∞) halmazon.
Ugyanis, itt korlátos a deriváltja:
Ezért ha x ∈ [1,+∞), akkor
Példa. A mindenhol értelmezett
függvény egyenletesen folytonos.
Ugyanis, a [-1,1] zárton a Heine-tétel miatt egyenletesen folytonos, azon kívül pedig
Folytonos differenciálhatóság
Tétel. -- Zárt intervallumon differenciálható függvény deriválfüggvénynek, nem lehet megszüntethető szakadása.
Ugyanis. Legyen f:[a,b]  R diff.-ható és tegyük fel, hogy létezik a
R diff.-ható és tegyük fel, hogy létezik a
és véges. Ekkor belátjuk, hogy ez a derivált a-beli helyettesítési értéke. Kiszámítjuk különbségi hányados határértéktét! Vegyük az xn = a + 1/n sorozatot (ill ennek [a,b]-beli részét). Minden [a,a+1/n] intervallumra felírhatjuk a Lagrange-tételt:
Ekkor a különbségi hányados függvényértékek sorozata egyenlő lesz a derivált egy függvényértéksorozatával, melyek így ugyanahhoz tartanak. De ez csak az f'(a) és a limuf' számok lehetnek, amik így egyenlők.
Ne keressünk tehát sem ugrást, sem megszüntethető szakadást a derivátlfüggvényen. Ellenben lehet korlátos másodfajú és a végtelen másodfajú szakadása.
6. Feladat. Határozzuk meg, hogy az alábbi függvények folytonosan differencálhatóak-e?
Megoldás. Mindegyiknél a metódus az, hogy (A) Meghatározzuk a deriváltfüggvény határértékét , (B) meghatározzuk a pontbeli deriváltat (C) Megnézzük, hogy egyenlők-e? Ha (A)-ban nincs határérték, akkor abból már kövevetkezik, hogy nem folyt. diff a függvény.
1.
nem folyt diff a 0-ban, mert nincs lim0 f', mert a második tag határértéke nem létezik (bár korlátos).
2.
nwm folyt diff a 0-ban, mert nincs lim0 f', mert a második tag határértéke nem létezik és nem is korlátos.
3.
Már csak a pontbeli deriváltat kell kiszámítani. Ez is 0.
A fenti tételen kívül több is igaz.
Állítás. Ha f:[a,b]  R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a fent említett tétel miatt a lima f' szám.
R folytonos a-ban, differenciálható a nyílton és létezik a derivált határértéke a-ban és ez véges szám, akkor f-nek létezik a deriváltja a-ban (és a deriváltja a fent említett tétel miatt a lima f' szám.
Bizonyítás. A későbbiekben igazolandó erős L'Hospital-tétel következménye. Tekintsük a különbségi hányados függvényt, legyen a L'H-beli "f" az f(x)-f(a), az x-a a g. Ekkor
azaz létezik a pontbeli derivált és ez a derivált határértéke.
Kérdés: hol használtuk fel, hogy az f függvény folytonos?
Tétel. -- Darboux-tétel -- Az f:[a,b]  R differenciálható függvény deriváltfüggvénye Darboux-tulajdonságú (azaz minden ilyen függvény két függvényértéke között minden értéket fölvesz).
R differenciálható függvény deriváltfüggvénye Darboux-tulajdonságú (azaz minden ilyen függvény két függvényértéke között minden értéket fölvesz).
Ugyanis, Legyen f'(a)<m<f'(b) és igazoljuk, hogy létezik ξ ∈ (a,b), hogy f'(ξ) = m. Vegyük a Lagrange-tételhez hasonlóan a
függvényt. Megállapíthatjuk, hogy tetszőleges x ∈ (a,b)-re
ha tehát keresünk g-hez stacionárius pontot (a,b)-n, akkor megtaláltuk ξ-t. Ilyet a Weierstrass-tétellel kereshetünk. g folytonos, így van maximuma és minimuma. Kell, hogy legyen belül is, ugyanis, ha csak kívül venné fel a szélsőértékeit, akkor a következő történne. g'(a) < 0, így a-ban g lokálisan csökken, hiszen ekkor van olyan kis intervallum, ahol az a-beli különbségihányados függvény negatív, azaz
ugyanekkor egy kis környzetben b-körül a függvény szintén lokálisan, hiszen
és így
Sem a-ban, sem b-ben ezek szerint nem lehet a ξ minimum, így annak belül kell lennie. Ekkor viszont alkalmazható a Fermat-tétel, mellyel:
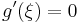 , azaz
, azaz 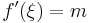
Feladat. Igaz-e?
- R
 R differenciálható függvény deriváltfüggvénye minden zárt és korlátos intervallumon felveszi minimumát és maximumát.
R differenciálható függvény deriváltfüggvénye minden zárt és korlátos intervallumon felveszi minimumát és maximumát.
- Ha az R
 R differenciálható függvény deriváltfüggvénye negatív és pozitív értékeket is felvesz, akkor van a driváltnak zérushelye.
R differenciálható függvény deriváltfüggvénye negatív és pozitív értékeket is felvesz, akkor van a driváltnak zérushelye.
- R
 R differenciálható függvény deriváltfüggvénye korlátos, akkor létezik olyan L szám, hogy minden x,y-ra: |f(x)-f(y)| < L|x-y|.
R differenciálható függvény deriváltfüggvénye korlátos, akkor létezik olyan L szám, hogy minden x,y-ra: |f(x)-f(y)| < L|x-y|.
- A deriválható függvények egyenletesen folytonosak.
- Korlátos és zárt intervallumon differenciálható függvények egyenletesen folytonos.
- A korlátos deriválttal rendelkező függvények egyenletesen folytonosak.
Inverzfüggvénytétel R-re
Tétel -- Globális inverzfüggvény-tétel -- Ha f: I  R függvény folytonosan differenciálható és f' sehol se nulla, akkor
R függvény folytonosan differenciálható és f' sehol se nulla, akkor
- f invertálható
- f inverze folytonos (f homeomorfizmus)
- f inverze deriválható (f diffeomorfizmus)
- minden x ∈ I-re
Megjegyzés. Részeletesebb indoklás azt is kimutatja, hogy a derivált folytonossága nem szükséges (bár nem árt :).
Bizonyítás. 1) A derivált mindenhol azonos előjelű, ellenkező esetben lenne két hely, ahol különböző, de a Darboux-tétel miatt akkor lenne zérushelye is a deriváltnak, ami ellentmond a feltételeknek. Tehát f szigorúan monoton, így invertálható.
2) Minden a ∈ I pontban a derivált nem nulla és folytonos, így létezik olyan környzete, melyben a derivált mindenhol egy L pozitív számál nagyobb. Ezért a Lagrange-tétel miatt a környzet bármely két x1, x2 pontjára:
Emiatt az x=f-1(y) áttéréssel:
azaz
azaz az inverz lipschitzes a környzetben, azaz a pontban folytonos. 3) 4) ezt egyszerre igazoljuk. Az u-beli diffhatóság miatt:
Itt az
függvény akkor lesz folytonos és v-ben eltűnő, ha maga f-1 is folytonos v-ben.
Példa. Igazoljuk, hogy létezik a sin inverze a [-π/2,π/2]-n és az inverz folytonos a [-1,1]-en (ez az arcsin) ezen kívül az inverz deriválható a belső pontokban!
Ugyanis. [-π/2,π/2]-n a sin szigorúan monoton nő és inverz képe [-1,1]. Emiatt ez folytonos is és az inverzfüggvény-tétel miatt a nyílton differenciálható, ugyanis
az inverze:
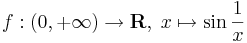
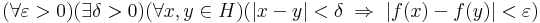
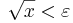
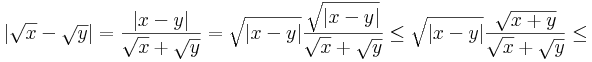
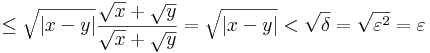
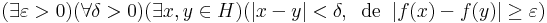
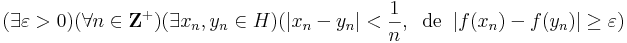
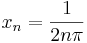
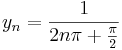
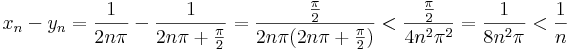
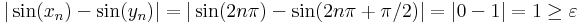
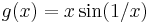
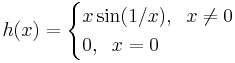
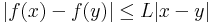
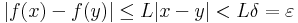
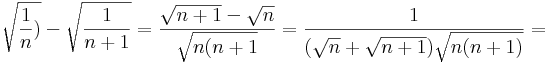
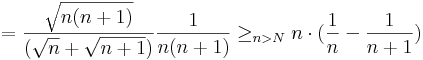
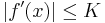
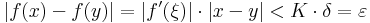
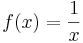
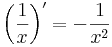
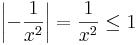
![f(x)=\cos\sqrt[3]{x}\,](/upload/math/0/4/3/043f3e44a6bee2a700990441696423c0.png)
![|f'(x)|=|\sin(\sqrt[3]{x})\cdot\frac{1}{3\sqrt[3]{x^2}}|\leq 1\cdot \frac{1}{3}=\frac{1}{3}](/upload/math/9/4/3/943cdc5854e013e705fad009d3b99f95.png)
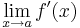
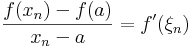
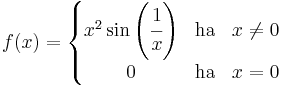
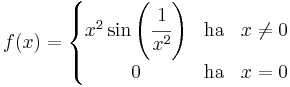
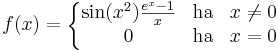
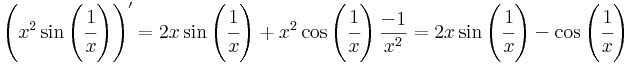
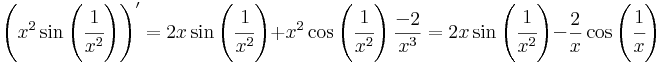
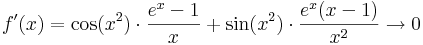
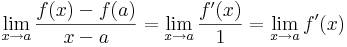
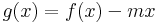
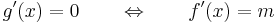
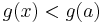
![\frac{g(x)-g(b)}{x-b}>0\quad\quad(x\in(b-\delta,b])](/upload/math/6/5/f/65f6c3b27b79722e89f76bf2f60b54ee.png)