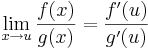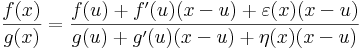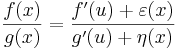Matematika A1a 2008/10. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Gyenge L'Hospital-szabály) |
||
| 3. sor: | 3. sor: | ||
==Gyenge L'Hospital-szabály== | ==Gyenge L'Hospital-szabály== | ||
| − | Legyenek ''f'' és ''g'': ''A'' <math>\to</math> '''R''' valós-valós függvények, ''u'' ∈ ''A'' ∩ | + | Legyenek ''f'' és ''g'': ''A'' <math>\to</math> '''R''' valós-valós függvények, ''u'' ∈ ''A'' ∩ ''A'' ', ''f''(u)=''g''(u)=0, mindkettő differenciálható ''u''-ban és g'(u) ≠ 0. Ekkor létezik a lim<sub>u</sub>(''f''/''g''), és |
:<math>\lim\limits_{x\to u}\frac{f(x)}{g(x)}=\frac{f'(u)}{g'(u)}</math> | :<math>\lim\limits_{x\to u}\frac{f(x)}{g(x)}=\frac{f'(u)}{g'(u)}</math> | ||
''Ugyanis,''' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az ''u''-hoz olyan ε, η: ''A'' <math>\to</math> '''R''', hogy minden ''x'' ∈ ''A'' ∩ Dom(''f''/''g'')-ra | ''Ugyanis,''' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az ''u''-hoz olyan ε, η: ''A'' <math>\to</math> '''R''', hogy minden ''x'' ∈ ''A'' ∩ Dom(''f''/''g'')-ra | ||
| − | <math>\frac{f(x)}{g(x)}=\frac{f(u)+f'(u)(x-u)+\varepsilon(x)(x-u)}{g(u)+g'(u)(x-u)+\eta(x)(x-u)}</math> | + | :<math>\frac{f(x)}{g(x)}=\frac{f(u)+f'(u)(x-u)+\varepsilon(x)(x-u)}{g(u)+g'(u)(x-u)+\eta(x)(x-u)}</math> |
| − | és ∃lim<sub>u</sub>ε=ε(u)=0, ∃lim<sub>u</sub>η=η(u)=0. Emiatt | + | és ∃lim<sub>u</sub>ε=ε(u)=0, ∃lim<sub>u</sub>η=η(u)=0. Emiatt és ''f''(u)=''g''(u)=0 miatt |
| + | :<math>\frac{f(x)}{g(x)}=\frac{f'(u)+\varepsilon(x)}{g'(u)+\eta(x)}</math> | ||
| + | Aminek a határéttéke, ha ''x'' tart ''u''-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget. | ||
==Lagrange-tétel== | ==Lagrange-tétel== | ||
A lap 2008. november 25., 00:42-kori változata
Gyenge L'Hospital-szabály
Legyenek f és g: A 
R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a limu(f/g), és
Ugyanis,' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az u-hoz olyan ε, η: A R, hogy minden x ∈ A ∩ Dom(f/g)-ra
és ∃limuε=ε(u)=0, ∃limuη=η(u)=0. Emiatt és f(u)=g(u)=0 miatt
Aminek a határéttéke, ha x tart u-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget.
Lagrange-tétel
Legyen f: [a,b] R differenciálható függvény.
