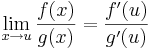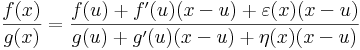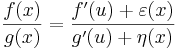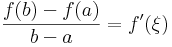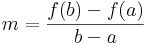Matematika A1a 2008/10. gyakorlat
Mozo (vitalap | szerkesztései) a (→Gyenge L'Hospital-szabály) |
Mozo (vitalap | szerkesztései) (→Fermat-féle szélsőértéktétel) |
||
| 18. sor: | 18. sor: | ||
==Fermat-féle szélsőértéktétel== | ==Fermat-féle szélsőértéktétel== | ||
| − | Ha ''f'' valós-valós függvény és ''f'' differenciálható az ''u'' ∈ int Dom(''f'') pontban és ''f''-nek ''u''-ban lokális szélsőértéke van, akkor | + | '''Tétel''' -- Differenciálható függvény belső pontbeli szélsőértéke létezésének szükséges feltétele -- Ha ''f'' valós-valós függvény és ''f'' differenciálható az ''u'' ∈ int Dom(''f'') pontban és ''f''-nek ''u''-ban lokális szélsőértéke van, akkor |
:<math>f'(u)=0,</math> | :<math>f'(u)=0,</math> | ||
| 25. sor: | 25. sor: | ||
Most az elsőt osszuk le &deta;<sub>n</sub>-nel, a másodikat -&deta;<sub>n</sub>-nel. Ekkor: | Most az elsőt osszuk le &deta;<sub>n</sub>-nel, a másodikat -&deta;<sub>n</sub>-nel. Ekkor: | ||
:<math>0\leq\frac{f(u+\delta_n)-f(u)}{\delta_n}\to f'(u)\,</math> és <math>f'(u)\leftarrow\frac{f(u-\delta_n)-f(u)}{-\delta_n}\leq 0\,</math> | :<math>0\leq\frac{f(u+\delta_n)-f(u)}{\delta_n}\to f'(u)\,</math> és <math>f'(u)\leftarrow\frac{f(u-\delta_n)-f(u)}{-\delta_n}\leq 0\,</math> | ||
| + | S mivel, ha egy sorozat csupa nemnegatív (nempozitív), akkor a határértéke is ilyen, ezért: | ||
| + | :<math>0\leq f'(u)\leq 0\,</math> azaz <math>f'(u)=0\,</math> | ||
| + | |||
| + | '''2. Feladat.''' Igaz-e? | ||
| + | # Ha ''f'' differenciálható az ''u'' ∈ int Dom(f)-ben és f'(u)=0, akkor ott szélsőértéke van. | ||
| + | # Ha ''f'' differenciálható az ''u'' ∈ Dom(f)-ben és ott szélső értéke van, akkor f'(u)=0. | ||
| + | # Ha '''f''': [a,b] <math>\to</math> '''R''' monoton és létezik f'(b) és = 0, akkor ott lokális szélsőértéke van (itt f'(b)-n a baloldali deriváltat értjük). | ||
| + | # Ha ''f''-nek az ''u'' ∈ int Dom(f)-ben szélsőértéke van, akkor f'(u)=0. | ||
| + | |||
| + | ''Megoldás.'' | ||
| + | |||
| + | # Nem igaz. Ellenpélda: f(x)=x<sup>3</sup> és ''u'' = 0. Itt ugyanis ''u'' ∈ int Dom(f), f'(0)=0, de nincs szélsőértéke f-nek. A derivált zárushelye ugyanis nem elégséges feltétele a szélsőértéknek. | ||
| + | # Nem igaz. [0,1] zárton az f(x)=x-nek szélsőértéke a 0, de 0-ban a jobboldali derivált 1. | ||
| + | # Igaz. Még akkor is, ha f'(b) nem nulla, pusztán a monotonitás következménye. | ||
| + | # Nem igaz, mert még az se biztos, hogy létezik a derivált. Ellenpélda: f(x)=|x|, u=0 | ||
==Lagrange-tétel== | ==Lagrange-tétel== | ||
A lap 2008. november 25., 10:51-kori változata
Gyenge L'Hospital-szabály
Legyenek f és g: A 
R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a limu(f/g), és
Ugyanis,' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az u-hoz olyan ε, η: A R, hogy minden x ∈ A ∩ Dom(f/g)-ra
és ∃limuε=ε(u)=0, ∃limuη=η(u)=0. Emiatt és f(u)=g(u)=0 miatt
Aminek a határéttéke, ha x tart u-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget.
1. Feladat.
Fermat-féle szélsőértéktétel
Tétel -- Differenciálható függvény belső pontbeli szélsőértéke létezésének szükséges feltétele -- Ha f valós-valós függvény és f differenciálható az u ∈ int Dom(f) pontban és f-nek u-ban lokális szélsőértéke van, akkor
- f'(u) = 0,
Tipikus átvitelielves tétel, hisz a "határérték" létezését tudjuk, csak az értékét kell kiszámolnunk. Tegyük fel, hogy u-ban minimum van. Legyen (δn) az 0-hoz tartó pozitív sorozat, mely minden n-re δn + u, u- δn ∈ Dom(f). Ekkor
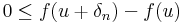és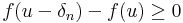 
Most az elsőt osszuk le &deta;n-nel, a másodikat -&deta;n-nel. Ekkor:
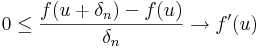és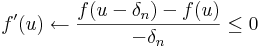 
S mivel, ha egy sorozat csupa nemnegatív (nempozitív), akkor a határértéke is ilyen, ezért:
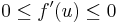azaz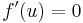 
2. Feladat. Igaz-e?
- Ha f differenciálható az u ∈ int Dom(f)-ben és f'(u)=0, akkor ott szélsőértéke van.
- Ha f differenciálható az u ∈ Dom(f)-ben és ott szélső értéke van, akkor f'(u)=0.
- Ha f: [a,b] R monoton és létezik f'(b) és = 0, akkor ott lokális szélsőértéke van (itt f'(b)-n a baloldali deriváltat értjük).
- Ha f-nek az u ∈ int Dom(f)-ben szélsőértéke van, akkor f'(u)=0.
Megoldás.
- Nem igaz. Ellenpélda: f(x)=x3 és u = 0. Itt ugyanis u ∈ int Dom(f), f'(0)=0, de nincs szélsőértéke f-nek. A derivált zárushelye ugyanis nem elégséges feltétele a szélsőértéknek.
- Nem igaz. [0,1] zárton az f(x)=x-nek szélsőértéke a 0, de 0-ban a jobboldali derivált 1.
- Igaz. Még akkor is, ha f'(b) nem nulla, pusztán a monotonitás következménye.
- Nem igaz, mert még az se biztos, hogy létezik a derivált. Ellenpélda: f(x)=|x|, u=0
Lagrange-tétel
Legyen f: [a,b] R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy
Ugyanis, Legyen
Olyan g differenciálható függvény adunk meg, melynek pontosan olyan x helyen van nulla deriváltja, ahol f'(x)=m. Transzformáljuk el az f függvényt az l(x)=m(x-a) függvénnyel. Ezzel a g(x) = f(x) - l(x) olyan lesz, hogy g(a)=f(a)=g(b). 1) g folytonos, így a Weierstrass-tétel miatt felveszi mindkét típusú extrémumát. 2) van szélsőértéke a nyílt (a,b)-n. Esetszétválasztással. Ha max=min=f(a), akkor a függvény konstans, így van belül extrémum. Ha bármelyik nem f(a), akkor az a valamelyik nem lehet a-ban vagy b-ben (mert ezekben g f(a)). 3) alkalmazhatjuk a Fermat-féle szélsőértéktételt, így g'(ξ)=0, azaz f'(ξ) = m.
