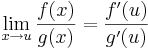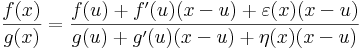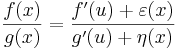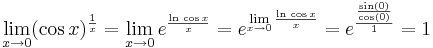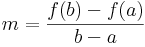Matematika A1a 2008/10. gyakorlat

_{<Matematika A1a 2008}

Gyenge L'Hospital-szabály

Legyenek f és g: A $\to$ R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a lim_u(f/g), és

$\lim\limits_{x\to u}\frac{f(x)}{g(x)}=\frac{f'(u)}{g'(u)}$

Ugyanis,' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az u-hoz olyan ε, η: A $\to$ R, hogy minden x ∈ A ∩ Dom(f/g)-ra

$\frac{f(x)}{g(x)}=\frac{f(u)+f'(u)(x-u)+\varepsilon(x)(x-u)}{g(u)+g'(u)(x-u)+\eta(x)(x-u)}$

és ∃lim_uε=ε(u)=0, ∃lim_uη=η(u)=0. Emiatt és f(u)=g(u)=0 miatt

$\frac{f(x)}{g(x)}=\frac{f'(u)+\varepsilon(x)}{g'(u)+\eta(x)}$

Aminek a határéttéke, ha x tart u-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget.

Példa.

$\lim\limits_{x\to 0} (\cos x)^{\frac{1}{x}}=\lim\limits_{x\to 0} e^{\frac{\mathrm{ln}\,\cos x}{x}}= e^{\lim\limits_{x\to 0}\frac{\mathrm{ln}\,\cos x}{x}}=e^{\frac{\frac{\sin(0)}{\cos (0)}}{1}}=1$

Fermat-féle szélsőértéktétel

Ha f valós-valós függvény és f differenciálható az u ∈ int Dom(f) pontban és f-nek u-ban lokális szélsőértéke van, akkor

f'(u) = 0,

Tipikus átvitelielves tétel, hisz a "határérték" létezését tudjuk, csak az értékét kell kiszámolnunk. Tegyük fel, hogy u-ban minimum van. Legyen (δ_n) az 0-hoz tartó pozitív sorozat, mely minden n-re δ_n + u, u- &deta;_n ∈ Dom(f). Ekkor

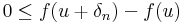$0\leq f(u+\delta_n)-f(u)\,$ és $f(u-\delta_n)-f(u)\geq 0\,$

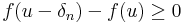
Most az elsőt osszuk le &deta;_n-nel, a másodikat -&deta;_n-nel. Ekkor:

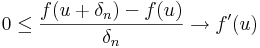$0\leq\frac{f(u+\delta_n)-f(u)}{\delta_n}\to f'(u)\,$ és $f'(u)\leftarrow\frac{f(u-\delta_n)-f(u)}{-\delta_n}\leq 0\,$

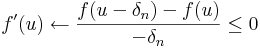
Lagrange-tétel

Legyen f: [a,b] $\to$ R differenciálható függvény. Ekkor létezik olyan ξ ∈ (a,b), hogy

$\frac{f(b)-f(a)}{b-a}=f'(\xi)\,$

Ugyanis, Legyen

$m=\frac{f(b)-f(a)}{b-a}\,$

Olyan g differenciálható függvény adunk meg, melynek pontosan olyan x helyen van nulla deriváltja, ahol f'(x)=m. Transzformáljuk el az f függvényt az l(x)=m(x-a) függvénnyel. Ezzel a g(x) = f(x) - l(x) olyan lesz, hogy g(a)=f(a)=g(b). 1) g folytonos, így a Weierstrass-tétel miatt felveszi mindkét típusú extrémumát. 2) van szélsőértéke a nyílt (a,b)-n. Esetszétválasztással. Ha max=min=f(a), akkor a függvény konstans, így van belül extrémum. Ha bármelyik nem f(a), akkor az a valamelyik nem lehet a-ban vagy b-ben (mert ezekben g f(a)). 3) alkalmazhatjuk a Fermat-féle szélsőértéktételt, így g'(ξ)=0, azaz f'(ξ) = m.