Matematika A1a 2008/11. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Határozott integrál) |
||
| 12. sor: | 12. sor: | ||
Az [a,b] összes '''Riemann-felosztásai halmazát''' RF[a,b] jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes részintervallum hossza kisebb egy δ > 0 pozitív számnál, azt RF<sub>δ</sub>[a,b] jelöli, azt a halmazt az [a,b] összes '''δ-nál finomabb Riemann-felosztásának''' nevezük. | Az [a,b] összes '''Riemann-felosztásai halmazát''' RF[a,b] jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes részintervallum hossza kisebb egy δ > 0 pozitív számnál, azt RF<sub>δ</sub>[a,b] jelöli, azt a halmazt az [a,b] összes '''δ-nál finomabb Riemann-felosztásának''' nevezük. | ||
| − | Egy ''f'', az [a,b]-n értelmezett függvény '''Riemann-közelítő összegén''' a | + | Egy ''f'', az [a,b]-n értelmezett függvény egy '''Riemann-közelítő összegén''' a |
| − | :<math>\ | + | :<math>\sigma_f(\eta)=\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])\cdot|x_i-x_{i-1}|)</math> |
ahol η a fenti jelölésekkel az [a,b] egy Riemann-felosztása. | ahol η a fenti jelölésekkel az [a,b] egy Riemann-felosztása. | ||
| 19. sor: | 19. sor: | ||
'''Definíció.''' Legyen ''f'':[a,b] <math>\to</math> '''R'''egy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy ''f'' '''Riemann-integrálható''' és integrálja az I valós szám, ha | '''Definíció.''' Legyen ''f'':[a,b] <math>\to</math> '''R'''egy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy ''f'' '''Riemann-integrálható''' és integrálja az I valós szám, ha | ||
| − | :<math>(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}[a,b])(|\ | + | :<math>(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}[a,b])(|\sigma_f(\eta)-I|< \varepsilon)</math> |
Belátható, hogy ha ''f'' integrálható, akkor I egyértelmű és ekkor ennek a számnak a jelölésére az | Belátható, hogy ha ''f'' integrálható, akkor I egyértelmű és ekkor ennek a számnak a jelölésére az | ||
:<math>\int f</math>, vagy az <math>\int \limits_{a}^{b}f(x)\,\mathrm{d}x</math> | :<math>\int f</math>, vagy az <math>\int \limits_{a}^{b}f(x)\,\mathrm{d}x</math> | ||
szimbólum szolgál. | szimbólum szolgál. | ||
| + | |||
| + | Az integrál lényegében a függvénygörbe alatti terület. Integrálható függvény esetén létezik ez a terület, azaz a Riemann-felosztást egyre finomabbra véve. | ||
[[Kategória:Matematika A1]] | [[Kategória:Matematika A1]] | ||
A lap 2008. december 5., 20:14-kori változata
Határozott integrál
Az egyváltozós analízis történetileg kialakult két jellegzetes témaköre közül az egyik az érintőproléma (lényegében a differenciálelmélet) a másik a területszámítás problémája, vagy régies elnevezéssel a kvadratúra-feldat (ami lényegében az integrálelmélet). Most a kvadratúra, azaz a függvénygörbe alatti terület definícióját adjuk meg. Ehhez azonban néhény segédfogalmat kell megismernünk.
Az [a,b] korlátos és zárt intervallum egy Riemann-felosztásán nem mást értünk mint egy olyan kiválasztófüggvényt, mely az [a,b]-t unióként előállító, egymásba nem nyúló intervallumokból álló halmaz minden egyes eleméhez egy az adott elemben lévő elemet rendel, azaz egy olyan
![\eta:\{[x_0,x_1],[x_2,x_3], ..., [x_{n-1},x_n] \}\to [a,b]\,](/upload/math/4/7/6/476cb30799b8150e22a3bbef00e5cfff.png)
függvényt, melyre:
- n olyan véges természetes szám, hogy x0 = a < x1 < x2 < ... < xn = b és
- minden J ∈ Dom(η) esetén
.
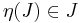Az [a,b] összes Riemann-felosztásai halmazát RF[a,b] jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes részintervallum hossza kisebb egy δ > 0 pozitív számnál, azt RFδ[a,b] jelöli, azt a halmazt az [a,b] összes δ-nál finomabb Riemann-felosztásának nevezük.
Egy f, az [a,b]-n értelmezett függvény egy Riemann-közelítő összegén a
![\sigma_f(\eta)=\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])\cdot|x_i-x_{i-1}|)](/upload/math/a/4/d/a4db058bcff2cbe8bb2d424ae853e44c.png)
ahol η a fenti jelölésekkel az [a,b] egy Riemann-felosztása.
Ekkor már definiálhatjuk az integrálhatóságot:
Definíció. Legyen f:[a,b] 
Regy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az I valós szám, ha
![(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}[a,b])(|\sigma_f(\eta)-I|< \varepsilon)](/upload/math/a/d/e/adefce08419bf5508ef3b14d65782293.png)
Belátható, hogy ha f integrálható, akkor I egyértelmű és ekkor ennek a számnak a jelölésére az
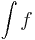, vagy az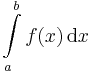 
szimbólum szolgál.
Az integrál lényegében a függvénygörbe alatti terület. Integrálható függvény esetén létezik ez a terület, azaz a Riemann-felosztást egyre finomabbra véve.
