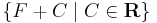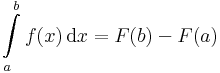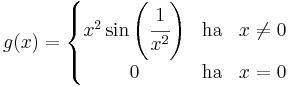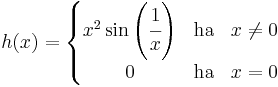Matematika A1a 2008/11. gyakorlat
Mozo (vitalap | szerkesztései) a (→Az integrálfüggvény differenciálhatósága) |
Mozo (vitalap | szerkesztései) (→Az integrálfüggvény differenciálhatósága) |
||
| 123. sor: | 123. sor: | ||
'''Tétel.''' -- A kalkulus fundamentális tétele I. -- Legyen ''f'':[a,b] <math>\to</math> '''R''' integrálható. Ha f folytonos az ''u'' ∈ [a,b] pontban, akkor ∫ f differenciálható ''u''-ban és | '''Tétel.''' -- A kalkulus fundamentális tétele I. -- Legyen ''f'':[a,b] <math>\to</math> '''R''' integrálható. Ha f folytonos az ''u'' ∈ [a,b] pontban, akkor ∫ f differenciálható ''u''-ban és | ||
:<math>\left(\int f\right)'(u)=f(u)\,</math> | :<math>\left(\int f\right)'(u)=f(u)\,</math> | ||
| + | |||
| + | ''Bizonyítás.'' ''f'' folytonos ''u''-ban, ezért tetszőleges ε > 0-ra létezik olyan δ > 0, hogy f|<sub>B(δ,u)</sub> ⊆ B<sub>ε</sub>(f(u)), azaz: | ||
| + | :<math>f(u)-\varepsilon \leq \inf f|_{\mathrm{B}_{\delta}(u)}\leq \sup f|_{\mathrm{B}_{\delta}(u)}\leq f(u)+\varepsilon</math> | ||
| + | Írjuk fel a deriváltra a különbségi hányadost! Legyen x,y olyan, hogy az u δ sugarú környezetébe esik. Ekkor az integrál intervallum szerinti additivitása miatt: | ||
| + | |||
| + | :<math>\frac{\int\limits_{a}^yf-\int\limits_{a}^x f}{y-x}=\frac{\int\limits_{x}^yf}{y-x}</math> | ||
| + | Ha most a tirviális alsó és felső becslést vesszük: | ||
| + | <math>f(u)- \varepsilon\inf f|_{[x,y]=\frac{\inf f|_{[x,y]}\cdot (y-x)}{y-x}\leq\frac{\int\limits_{x}^yf}{y-x}\leq \frac{\sup f|_{[x,y]}\cdot (y-x)}{y-x}\sup f|_{[x,y]}\leq f(u)+ \varepsilon</math> | ||
| + | s mivel ε tetszőleges volt, ezért f(u) nem más, mint az integrálfüggvény u-beli különbségi háényadosának határértéke (az x=u helyettesítéssel). QED | ||
| + | |||
| + | Látható, hogy a bizonyításban többet láttunk be. Egyfajta u-beli egyenletes differenciálatóságot, az úgy nevezett erős differenciálhatóságot. | ||
==Primitívfüggvények== | ==Primitívfüggvények== | ||
A lap 2008. december 7., 10:12-kori változata
Tartalomjegyzék |
Határozott integrál
Az egyváltozós analízis történetileg kialakult két jellegzetes témaköre közül az egyik az érintőproléma (lényegében a differenciálelmélet) a másik a területszámítás problémája, vagy régies elnevezéssel a kvadratúra-feldat (ami lényegében az integrálelmélet). Most a kvadratúra, azaz a függvénygörbe alatti terület definícióját adjuk meg. Ehhez azonban néhény segédfogalmat kell megismernünk.
Az [a,b] korlátos és zárt intervallum egy Riemann-felosztásán nem mást értünk mint egy olyan kiválasztófüggvényt, mely az [a,b]-t unióként előállító, egymásba nem nyúló intervallumokból álló halmaz minden egyes eleméhez egy az adott elemben lévő elemet rendel, azaz egy olyan
függvényt, melyre:
- n olyan véges természetes szám, hogy x0 = a < x1 < x2 < ... < xn = b és
- minden J ∈ Dom(η) esetén
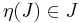 .
.
Az [a,b] összes Riemann-felosztásai halmazát RF[a,b] jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes részintervallum hossza kisebb egy δ > 0 pozitív számnál, azt RFδ[a,b] jelöli, azt a halmazt az [a,b] összes δ-nál finomabb Riemann-felosztásának nevezük.
Egy f, az [a,b]-n értelmezett függvény egy Riemann-közelítő összegén a
ahol η a fenti jelölésekkel az [a,b] egy Riemann-felosztása.
Ekkor már definiálhatjuk az integrálhatóságot:
Definíció. Legyen f:[a,b]  Regy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az I valós szám, ha
Regy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az I valós szám, ha
Belátható, hogy ha f integrálható, akkor I egyértelmű és ekkor ennek a számnak a jelölésére az
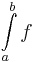 , vagy az
, vagy az 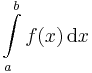
szimbólum szolgál.
Az [a,b] intervallumon Riemann-integrálható függvények halmazát R[a,b] jelöli.
Az integrál lényegében a függvénygörbe alatti terület. Integrálható függvény esetén létezik ez a terület, azaz a Riemann-felosztást egyre finomabbra véve, a Riemann-közelítő összeg minden előre megadott legnagyobb ε eltérésnél közelebb kerül I-hez.
Világos, hogy ha egy függvény integrálható, akkor minden részintervallumán is integrálható (hisz ekkor azokat a felosztásokat kell venni, amik a részintervallumon belül is felosztások, és persze ezek szerint is képezve a határátmenetet, létező határértéket kapunk). Minhogy az integrál egy szám, integrálható f esetén értelmes ha definiáljuk a következő, úgy nevezett integrálfüggvényt (vagy a-ban eltűnő integrálfüggvényt):
Definíció szerinti példák
1. Példa. Jóformán az egyetlen függvény, aminek az integrálhatóságát a definíció alapján könnyen igazolni tudjuk, az a konstans függvény. Az f(x) = c esetén a kiválaszott pontok mindig c függvényértékűek, és az összes közelítő összeg mindig
azaz
Már ezzel is azonban fel tudunk írni egy integrálfüggvényt: f:[a,b] R, f ≡ c esetén:
R, f ≡ c esetén:
2. Példa. Nem minden függvény integrálható.
2. a. Zárjuk le a reciprok függvényt egy ponttal:
(Riemann az 1854-es habilitációs dolgozatában definiálta és vizsgálta a most Riemann-integrálhatóságnak nevezett fogalmaz, mindazonáltal az integrál első, a szigorúság követelményének eleget tévő definícióját Cauchy adta (1821) az intuitívet pedig Leibniz.) Ez a függvény nem integrálható, mert akármilyen fimon intervallumfelosztás esetén, ha az első intervallumot δ hosszúra választjuk, definiálható egy η([x0,x1]) < δ2 érték, azaz f(η([x0,x1])) > 1/ δ2. Ekkor viszont az első téglalap területe 1/δ lesz, ami δ \to 0 esetén a +∞-be tart, azaz az összterület nem lesz véges.
2. b. Legyen f a Dirichlet-függvény:
ahol Q a racionális számok halmaza, R / Q pedig nyilván az irracionális. Ez a függvény nem Riemann-integrálható, bár korlátos, mert akármilyen finom intervallum-felbontás esetén van egy olyan Riemann-kiválasztó függvény, mely mindig racionális pontokat választ ki és ezáltal a közelítő összeg mindig 1 és olyan, mely mindig irracionálist, azaz ezzel a közelítő összeg 0. Mindig lesz tehát két olyan felbontás, mely összegek különbsége legalább 1.
A Riemann-inregrálhatóság szükséges és elégséges feltétele
Bár a Riemann-integrálhatóság általában könnyen kezeéhető fogalom, a következő tétel bizonyításához azonban az egyváltozós analízis szinte összes eszközét be kell vetni. Nem csoda, hogy csak 1905-ben fogalmazhatta meg Lebesgue, egy tágabb perspektívából szemlélve a Riemann-integrált.
Tétel. Legyen f: [a,b]  R korlátos és zárt intervallumon értelmezett függvény. f pontosan akkor integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
R korlátos és zárt intervallumon értelmezett függvény. f pontosan akkor integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
Itt Lebesgue-nullmértékűnek nevezünk egy H ⊆ R halmazt, ha minden ε > 0-hoz létezik olyan (In) intervallumsorozat, hogy ennek összhossza < ε és lefedi H-t.
Biztos nem nullmértékű például egy nemelfajuló intervallum, mert annak a mértéke az intervallum nemnulla hossza. De véges halmaz nullmértékű, mert lefedhető, egy határértékben eltűnő intervallumsorozat-rendszerrel. Belátható, hogy megszámlálható pont nullmértékű halmazt alkot. Konkrétan, könyen belátható, hogy az 1/n pontjai nullmértékű halmazt alkotnak.
Világos, hogy a Dirichlet-függvényes példa azért jó ellenpélda, mert ez a függvény [0,1]-en mindenhol szakad, azaz discon(Dir)=[0,1], melynek a mértéke 1.
Példa. Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. A konstrukció e következő. Először definiáljuk az ördög lépcsője függvényt:
A [0,1] intervallumot osszuk 3 részre és vegyük ki a belső nyílt harmadot. Ezen a szakaszon legyen a függvény értéke a bel végpont. Ismételjük a megmaradt két zárt intervallumra, ... Ami megmarad a halmazból, az az úgy nevezett Cantor-halmaz. A Cantor-halmaz kontinuum számosságúan végtelen, de Lebesgue-nullmértékű -- ezta a két dolgot persze nem bizonyítjuk. A függvény mindenhol deriválható és a deriváltja 0 (de nem intervallumon értelmezett: Dom = [0,1]\C). Ha most vesszük a deriváltfüggvényét és kiterjesztjük a C pontjaiban úgy, hogy ott 1 legyen az értéke, akkor ez egy kontinuum számosságú, de Lebesgue-nullmértékű halmazon szakadó, korlátos függvény, azaz integrálható. És az integrálja 0. Ebből is látható, hogy a fenti ekvivalenciatétel csodálatosan oldja meg, hogy bár a Riemann-felosztás véges, kontinuum számosságú, L-0-m. résszel is el tud bánni.
A Riemann-integrálhatóság néhány kritériuma
Részletezünk néhány hasznos esetet a fenti tételből.
-
![f\in \mathrm{R}[a,b]\;\Rightarrow\;f\in \mathrm{B}[a,b]](/upload/math/b/8/3/b83309f476aa7945359baebf79f1e9b7.png)
- csak korlátos függvények R-intgrálhatóak
-
![f\in \mathrm{R}[a,b]\;\Leftarrow\;f\in \mathrm{C}[a,b]](/upload/math/6/1/b/61b955edf5d07d91ba8d85640fc49029.png)
- (Cauchy) világos: ha folytonos, akkor nincs szakadási pontja, és korlátos a Weierstrass-tétel miatt
-
![f\in \mathrm{R}[a,b]\;\Leftarrow\;f\in \mathrm{M}[a,b]](/upload/math/f/0/3/f03e7b5351b87da25a7c01f433aa9c8d.png)
- monoton függvény R-integrálható (minden feltétel nélkül), amiatt a nem említett tétel miatt, hogy intervallumon értelmezett, monoton függvénynek csak megszámlálható szakadási pontja van, korlátos és zárt intervallumon pedig egy ilyen függvény korlátos.
Feladat. Intergálhatóak-e az alábbi függvények és ha igen, mi az integráljuk?
1.
Igen, mert folytonos (illetve legfeljebb csak 1 ponton szakad). Ezen kívül páratlan: |-x|sin(1/-x) = -|x|sin(1/x), emiatt az origóra szimmetrikus intervallumon az integrálja 0.
2.
Igen, mert monoton. Az integrálját elegendő egyetlen végtelenül finomodó felosztássorozathoz tartozó közelítő összegsorozat határértékeként számolni, hiszen ha ez nem konvergálna, akkor nem teljesülne a definícióban megkövetelt határérték létezése. Az intervallumot 2m részre osztjuk fel. Ekkor az összeg:
Ennek a határértéke a mértani sor összegképlete miatt:
3.
Megszámlálható sok szakadása van ugyan a függvénynek, de nem korlátosan a szakadások, így a függvény nem integrálható.
Az határozott intergál néhány tulajdonsága
- Intervallum szerinti additivitás.
- Integrandus szerinti additivitás.
- Integrandus szerinti monotonitás.
- Integrandus szerinti homogenitás.
Az integrálfüggvény differenciálhatósága
Az integrálfüggvény viselkedését vizsgálva meglepő következtetésre juthatunk.
Példa. Vegyük az alábbi lépcsős függvényt:
írjuk fel az integrálfüggvénét tudva tudván, hogy az nem más mint a területfüggvény:
Ábrázolva azt kapjuk, hogy T képe egy törött vonal, folytonos és mindehol, ahol nem törik a deriváltja az integrandus. T diff.-ható a [0,1)U(1,2] halmazon és
Az integrandus folytonossági helyein az integrálfüggvény valóban differenciálható. Az alábbi tételt az analízis első alaptételének szokás nevezni.
Tétel. -- A kalkulus fundamentális tétele I. -- Legyen f:[a,b]  R integrálható. Ha f folytonos az u ∈ [a,b] pontban, akkor ∫ f differenciálható u-ban és
R integrálható. Ha f folytonos az u ∈ [a,b] pontban, akkor ∫ f differenciálható u-ban és
Bizonyítás. f folytonos u-ban, ezért tetszőleges ε > 0-ra létezik olyan δ > 0, hogy f|B(δ,u) ⊆ Bε(f(u)), azaz:
Írjuk fel a deriváltra a különbségi hányadost! Legyen x,y olyan, hogy az u δ sugarú környezetébe esik. Ekkor az integrál intervallum szerinti additivitása miatt:
Ha most a tirviális alsó és felső becslést vesszük: Értelmezés sikertelen (formai hiba): f(u)- \varepsilon\inf f|_{[x,y]=\frac{\inf f|_{[x,y]}\cdot (y-x)}{y-x}\leq\frac{\int\limits_{x}^yf}{y-x}\leq \frac{\sup f|_{[x,y]}\cdot (y-x)}{y-x}\sup f|_{[x,y]}\leq f(u)+ \varepsilon
s mivel ε tetszőleges volt, ezért f(u) nem más, mint az integrálfüggvény u-beli különbségi háényadosának határértéke (az x=u helyettesítéssel). QED
Látható, hogy a bizonyításban többet láttunk be. Egyfajta u-beli egyenletes differenciálatóságot, az úgy nevezett erős differenciálhatóságot.
Primitívfüggvények
Definíció. Azt mondjuk, hogy az f:[a,b]  R függvénynek primitív függvénye az F:[a,b]
R függvénynek primitív függvénye az F:[a,b] R differenciálható függvény, ha F' = f.
R differenciálható függvény, ha F' = f.
Világos, hogy ha F primitív függvénye f-nek, akkor akármilyen konstans C-vel F + C is primitív függvénye f-nek, hisz (F + C)'= F' = f. Ennél több is igaz. Ha f-nek primitívfüggvénye F, akkor f összes primitívfüggvénye F + C alakú, ahol C tetszőleges valós szám. Ez az alábbi fontos tétel közvetlen következménye:
Tétel. Ha az F:[a,b] R differenciálható függvény olyan, hogy F' ≡ 0, akkor létezik olyan C valós szám, hogy F ≡ C.
R differenciálható függvény olyan, hogy F' ≡ 0, akkor létezik olyan C valós szám, hogy F ≡ C.
Bizonyítás. Egyszerűen a Lagrange-tételt kell alkalmazni F egy tetszőleges [a,x]-re történő leszűkítésétre:
azaz
QED
Ha tehát egyáltalán van f-nek van primitív függvénye és F ilyen, akkor ezek halmaza:
Talán fellengzősség, de a fenti tételt néha az integrálszámítás alaptételének nevezik. Ennek egy kiterjesztett formája azonban tényleg méltó erre a névre:
Tétel. Ha az F:[a,b] R differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és létezik olyan L szám, hogy minden x,y ∈ [a,b]-re |F(x) - F(y)| < L |x - y|, akkor F konstans.
R differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és létezik olyan L szám, hogy minden x,y ∈ [a,b]-re |F(x) - F(y)| < L |x - y|, akkor F konstans.
Az alábbi tétel szerint, amit szintén joggal neveznek a kalkulus fundamentális tételének, ha egy integrálható függvénynek van primitív függénye, akkor az integrálfüggvények és primitívfüggvények halmaza egybeesik, sőt:
Tétel. Newton--Leibniz-formula Legyen f:[a,b] R integrálható és létezzen primitív függvénye. Ekkor f mindnen F primitív függvényére:
R integrálható és létezzen primitív függvénye. Ekkor f mindnen F primitív függvényére:
Lényegesek ennek a tételnek a feltételei. Nézzük az eseteket!
++++++++++++++++++++++++++++++++++++++++++
+ létezik primitív függvénye + Dir
+ +
+ +
+ *********************************************************
+ g' * h' + R-integrálható *
+ * + *
+ * ############### + *
+ * # folytonos # + *
+ * # # + *
+ * ############### + Ent|[0,2] *
+ * + *
+ * + *
+++++++++++++++++*++++++++++++++++++++++++ *
* *
* *
* *
*********************************************************
A Dir Dirichlet-függvények nem létezik primitívfüggvénye, mert ha lenne olyan függvény, aminek ő a deriváltja lenne, akkor ő, mint deriváltfüggvény nem lenne Darboux-tulajdpnságú: két függvényértéke között nem mindent venne fel. Azt is megéztük, hogy R-integrálja sincs. (Bár Lebesgue-integrálja 0.)
Az Ent egészrész függvény integrálható (egy korlátos és zárt intevallumon), mert monoton, de nincs primitív függvénye, mert derivált nem ugorhat.
Legyen g : [-1,1]  R a következő:
R a következő:
Ekkor g differenciálható, így g'-nek g primitívfüggvénye, de tudjuk, hogy g'-nek nem korlátos másodfajú szakadésa van a 0-ban, így g' nem lehet integrálható.
Végül nézzünk példát olyan függvényre, mely nem folytonos, de értelmes rá a N--L-formula. Legyen h: [-1,1]  R a következő:
R a következő:
Ekkor g differenciálható, így g'-nek g primitívfüggvénye, és tudjuk, hogy g' korlátos és csak a 0-ban van egyetlen szakadása, így g' integrálható.
Megjegyezük, hogy a görbe alatti területet nem véges összegekkel, hanem végtelen sorral közelítő Lebesgue-integrál olyan általános, hogy ilyen vagy még általánosabban definiált értelmeben nem integrálható függvényt keresni már komoly matematikai/halmazelméleti kihívást jelent.
![\eta:\{[x_0,x_1],[x_2,x_3], ..., [x_{n-1},x_n] \}\to [a,b]\,](/upload/math/4/7/6/476cb30799b8150e22a3bbef00e5cfff.png)
![\sigma_f(\eta)=\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])\cdot|x_i-x_{i-1}|)](/upload/math/a/4/d/a4db058bcff2cbe8bb2d424ae853e44c.png)
![(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}[a,b])(|\sigma_f(\eta)-I|< \varepsilon)](/upload/math/a/d/e/adefce08419bf5508ef3b14d65782293.png)
![\int f:[a,b]\to \mathbf{R}, x\mapsto\int\limits_{a}^xf\,](/upload/math/3/2/1/32197d847adb794644364ba069a88472.png)
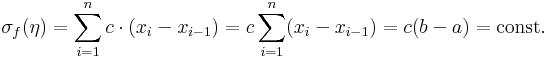
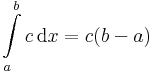
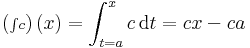
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{x}, & \mathrm{ha} & x\in (0,1] \\\\ 1854, & \mathrm{ha} & x=0 \end{matrix}\right.](/upload/math/f/e/2/fe28b4484356f462699457435a0cb0ad.png)
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in \mathbf{Q} \\\\ 0, & \mathrm{ha} & x\in \mathbf{R}\setminus\mathbf{Q} \end{matrix}\right.](/upload/math/a/c/3/ac329e8012056e15927ee566fbe98db2.png)
![f\in \mathrm{R}[a,b]\;\Leftrightarrow\;(f\in \mathrm{B}[a,b]\;\wedge\; \mathrm{m}(\mathrm{discon}(f))=0)](/upload/math/d/2/c/d2c21ed005e06a1ea4ae356da5bcd67c.png)
![f:[-1,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}|x|\sin(\frac{1}{x}), & \mathrm{ha} & x\ne 0 \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.](/upload/math/6/a/b/6ab08e2bf7e7ec46f393164c1e44b064.png)
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{2^{i+1}}, & \mathrm{ha} & \frac{1}{2^{i+1}}<x\leq\frac{1}{2^i} \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.](/upload/math/a/5/c/a5cad5a3691bdc5262070039cb1e2b8a.png)
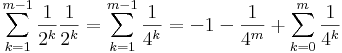
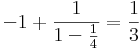
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{1+\sin(\frac{1}{x})}, & \mathrm{ha} & x\ne \frac{1}{-\frac{\pi}{2}+2k\pi},0\\\\ 0, & \mathrm{ha} & x= \frac{1}{\frac{-\pi}{2}+2k\pi},0\end{matrix}\right.](/upload/math/6/6/4/664caab5c66ee826755e5fbadea1a63f.png)
![f:[0,2]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in [0,1) \\\\ 2, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.](/upload/math/7/f/a/7fad0719708fc616be5c846dcd569210.png)
![T(x)=\left\{\begin{matrix}x\cdot 1, & \mathrm{ha} & x\in [0,1) \\\\ 1+2(x-1), & \mathrm{ha} & x\in [1,2] \end{matrix}\right\}=\left\{\begin{matrix}x, & \mathrm{ha} & x\in [0,1) \\\\ 1+2x, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.](/upload/math/c/1/2/c12dc345c60fde7473fb1d6a5d3793ff.png)
![T'=f|_{[0,1)\cup(1,2]}](/upload/math/5/5/8/5581144dddd6d5c01260374f851b3ad2.png)
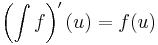
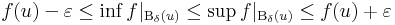
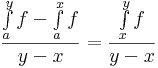
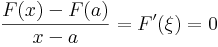
![F(a)=F(x)\,\quad\quad (x\in [a,b])](/upload/math/8/8/5/8854a00d6bd4ec6a3b6b485cea6de8be.png)