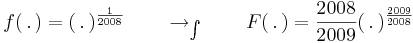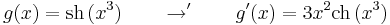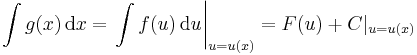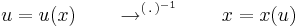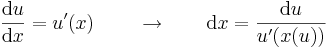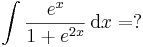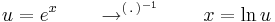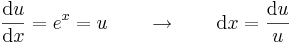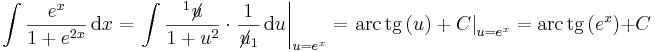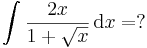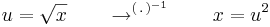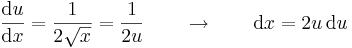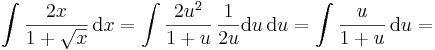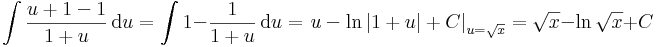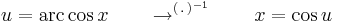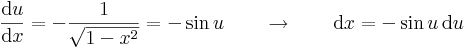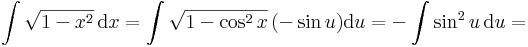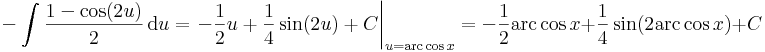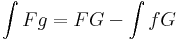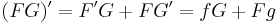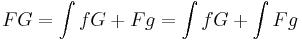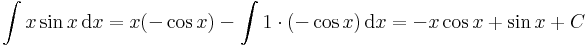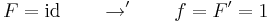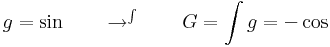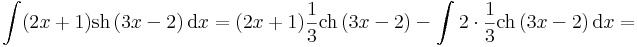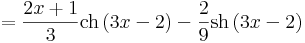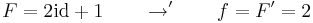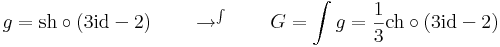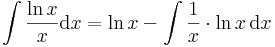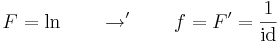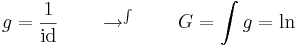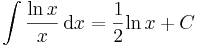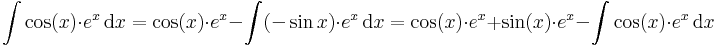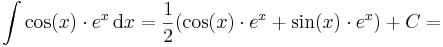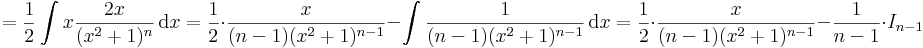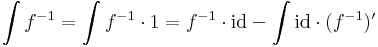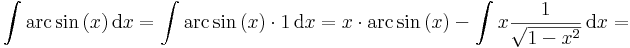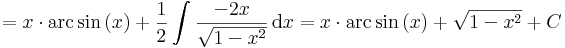Matematika A1a 2008/11. gyakorlat
Mozo (vitalap | szerkesztései) (→Az integrálfüggvény differenciálhatósága) |
Mozo (vitalap | szerkesztései) (→Példák) |
||
| (egy szerkesztő 43 közbeeső változata nincs mutatva) | |||
| 67. sor: | 67. sor: | ||
'''Példa.''' Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. A konstrukció e következő. Először definiáljuk az '''ördög lépcsője''' függvényt: | '''Példa.''' Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. A konstrukció e következő. Először definiáljuk az '''ördög lépcsője''' függvényt: | ||
| − | A [0,1] intervallumot osszuk 3 részre és vegyük ki a belső nyílt harmadot. Ezen a szakaszon legyen a függvény értéke | + | A [0,1] intervallumot osszuk 3 részre és vegyük ki a belső nyílt harmadot. Ezen a szakaszon legyen a függvény értéke 1/2. Ismételjük a megmaradt két zárt intervallumra, és az érték legyen ott 1/4 ill. 3/4. A fennmaradt részeket is osszuk, majd a középső harmad értéke mindig a két szélső közepe legyen... Ha csak a belső harmadokat vesszük, akkor ami megmarad a halmazból, az az úgy nevezett Cantor-halmaz. A Cantor-halmaz kontinuum számosságúan végtelen, de Lebesgue-nullmértékű -- ezt a két dolgot persze nem bizonyítjuk. A függvény mindenhol folytonos, a m.m- deriválható és a deriváltja 0 (de nem intervallumon értelmezett: Dom = [0,1]\C). Ha most vesszük a deriváltfüggvényét és kiterjesztjük a C pontjaiban úgy, hogy ott 1 legyen az értéke, akkor ez egy kontinuum számosságú, de Lebesgue-nullmértékű halmazon szakadó, korlátos függvény, azaz integrálható. És az integrálja 0. Ebből is látható, hogy a fenti ekvivalenciatétel csodálatosan oldja meg, hogy bár a Riemann-felosztás véges, kontinuum számosságú, L-0-m. résszel is el tud bánni. |
===A Riemann-integrálhatóság néhány kritériuma=== | ===A Riemann-integrálhatóság néhány kritériuma=== | ||
| 84. sor: | 84. sor: | ||
1. | 1. | ||
:<math>f:[-1,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}|x|\sin(\frac{1}{x}), & \mathrm{ha} & x\ne 0 \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.</math> | :<math>f:[-1,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}|x|\sin(\frac{1}{x}), & \mathrm{ha} & x\ne 0 \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.</math> | ||
| − | Igen, mert folytonos (illetve legfeljebb csak 1 ponton szakad). Ezen kívül páratlan: |-x|sin(1/-x) = -|x|sin(1/x), emiatt az origóra szimmetrikus intervallumon az integrálja 0 | + | Igen, mert folytonos (illetve legfeljebb csak 1 ponton szakad, miközben korlátos). Ezen kívül páratlan: |-x|sin(1/-x) = -|x|sin(1/x), emiatt az origóra szimmetrikus intervallumon az integrálja: |
| + | :<math>\int\limits_{-1}^1f(x)\,\mathrm{d}x=0</math> | ||
2. | 2. | ||
| 92. sor: | 93. sor: | ||
:<math>\sum\limits_{k=1}^{m-1}\frac{1}{2^k}\frac{1}{2^k}=\sum\limits_{k=1}^{m-1}\frac{1}{4^k}=-1-\frac{1}{4^{m}}+\sum\limits_{k=0}^{m}\frac{1}{4^k}\,</math> | :<math>\sum\limits_{k=1}^{m-1}\frac{1}{2^k}\frac{1}{2^k}=\sum\limits_{k=1}^{m-1}\frac{1}{4^k}=-1-\frac{1}{4^{m}}+\sum\limits_{k=0}^{m}\frac{1}{4^k}\,</math> | ||
Ennek a határértéke a mértani sor összegképlete miatt: | Ennek a határértéke a mértani sor összegképlete miatt: | ||
| − | :<math>-1+\frac{1}{1-\frac{1}{4}}=\frac{1}{3}</math> | + | :<math>\int\limits_{0}^1f(x)\,\mathrm{d}x=-1+\frac{1}{1-\frac{1}{4}}=\frac{1}{3}</math> |
3. | 3. | ||
| 98. sor: | 99. sor: | ||
:<math>f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{1+\sin(\frac{1}{x})}, & \mathrm{ha} & x\ne \frac{1}{-\frac{\pi}{2}+2k\pi},0\\\\ 0, & \mathrm{ha} & x= \frac{1}{\frac{-\pi}{2}+2k\pi},0\end{matrix}\right.</math> | :<math>f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{1+\sin(\frac{1}{x})}, & \mathrm{ha} & x\ne \frac{1}{-\frac{\pi}{2}+2k\pi},0\\\\ 0, & \mathrm{ha} & x= \frac{1}{\frac{-\pi}{2}+2k\pi},0\end{matrix}\right.</math> | ||
| − | Megszámlálható sok szakadása van ugyan a függvénynek, de nem korlátosan a szakadások, így a függvény nem integrálható | + | Megszámlálható sok szakadása van ugyan a függvénynek, de nem korlátosan a szakadások, így a függvény nem integrálható: |
| + | :<math>\not\exists\int\limits_{0}^1f(x)\,\mathrm{d}x</math> | ||
| − | ===Az határozott | + | ===Az határozott integrál néhány tulajdonsága=== |
| + | A következőkben feltesszük, hogy az f és g a formulákban szereplő intervallumokat tartalmazó valamely intervallumon Riemann-integrálható. | ||
| − | # Intervallum szerinti additivitás | + | # Intervallum szerinti additivitás: |
| − | # Integrandus szerinti additivitás | + | #:<math>\int\limits_{a}^b f+\int\limits_{b}^c f = \int\limits_{a}^c f</math> |
| + | # Integrandus szerinti additivitás: | ||
| + | #:<math>\int\limits_{a}^b f+\int\limits_{a}^b g = \int\limits_{a}^b f+g</math> | ||
# Integrandus szerinti monotonitás. | # Integrandus szerinti monotonitás. | ||
| − | # Integrandus szerinti homogenitás. | + | #:<math>f\leq g\quad\quad\Rightarrow\quad\quad\int\limits_{a}^b f\leq \int\limits_{a}^b g</math> |
| + | # Integrandus szerinti homogenitás: | ||
| + | #:<math>c\cdot \int\limits_{a}^b f= \int\limits_{a}^b cf\quad\quad(c\in\mathbf{R})</math> | ||
| + | # Abszolút becslés. | ||
| + | #: <math>\left|\int\limits_{a}^b f\right|\leq \int\limits_{a}^b |f|</math> | ||
| + | # Triviális alsó és felső becslés. | ||
| + | #: <math>(\inf f)\cdot(b-a)\leq \int\limits_{a}^b f\leq(\sup f)\cdot(b-a)</math> | ||
| + | # Eltolásinvariancia. | ||
| + | #:<math>\int\limits_{a+c}^{b+c} f(x-c)\,\mathrm{d}x= \int\limits_{a}^b f(x)\,\mathrm{d}x</math> | ||
| − | ===Az integrálfüggvény | + | ===Az integrálfüggvény néhány tulajdonsága=== |
Az integrálfüggvény viselkedését vizsgálva meglepő következtetésre juthatunk. | Az integrálfüggvény viselkedését vizsgálva meglepő következtetésre juthatunk. | ||
| 114. sor: | 127. sor: | ||
:<math>f:[0,2]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in [0,1) \\\\ 2, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.</math> | :<math>f:[0,2]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in [0,1) \\\\ 2, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.</math> | ||
| − | írjuk fel az | + | írjuk fel az integrálfüggvényét tudva-tudván, hogy az nem más mint a területfüggvény: |
| − | :<math>T(x)=\left\{\begin{matrix}x\cdot 1, & \mathrm{ha} & x\in [0,1) \\\\ 1+2(x-1), & \mathrm{ha} & x\in [1,2] \end{matrix}\right\}=\left\{\begin{matrix}x, & \mathrm{ha} & x\in [0,1) \\\\ | + | :<math>T(x)=\left\{\begin{matrix}x\cdot 1, & \mathrm{ha} & x\in [0,1) \\\\ 1+2(x-1), & \mathrm{ha} & x\in [1,2] \end{matrix}\right\}=\left\{\begin{matrix}x, & \mathrm{ha} & x\in [0,1) \\\\ 2x-1, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.</math> |
| − | Ábrázolva azt kapjuk, hogy T képe egy törött vonal, '''folytonos''' és mindehol, ahol nem törik a '''deriváltja az integrandus'''. T diff.-ható a [0,1)U(1,2] halmazon és | + | Ábrázolva, azt kapjuk, hogy T képe egy törött vonal, '''folytonos''' és mindehol, ahol nem törik, a '''deriváltja az integrandus'''. T diff.-ható a [0,1)U(1,2] halmazon és |
:<math>T'=f|_{[0,1)\cup(1,2]} </math> | :<math>T'=f|_{[0,1)\cup(1,2]} </math> | ||
| + | |||
| + | ====Az integrálfüggvény differenciálhatóságáról==== | ||
Az integrandus folytonossági helyein az integrálfüggvény valóban differenciálható. Az alábbi tételt az analízis első alaptételének szokás nevezni. | Az integrandus folytonossági helyein az integrálfüggvény valóban differenciálható. Az alábbi tételt az analízis első alaptételének szokás nevezni. | ||
| 133. sor: | 148. sor: | ||
s mivel ε tetszőleges volt, ezért f(u) nem más, mint az integrálfüggvény u-beli különbségi háényadosának határértéke (az x=u helyettesítéssel). QED | s mivel ε tetszőleges volt, ezért f(u) nem más, mint az integrálfüggvény u-beli különbségi háényadosának határértéke (az x=u helyettesítéssel). QED | ||
| − | Látható, hogy a bizonyításban többet láttunk be. Egyfajta u | + | Látható, hogy a bizonyításban többet láttunk be. Egyfajta u körüli "egyenletes differenciálatóságot", az úgy nevezett erős differenciálhatóságot. Ez azért lehet fontos, mert ha az integrálfüggény deriváltja nem nulla, akkor nem csak ő, de az inverze is Lipschitz-folytonos, amiből pedig az következik, hogy mind az i.f. mind az inverze nullmértékű halmazt nullmértékűbe képez. |
| − | És persze az integrálfüggvény "nagyon" folytonos, azaz létezik olyan L, hogy minden x,y ∈ [a,b]-re | + | ====Az integrálfüggvény Lipschitz-tulajdonsága==== |
| + | |||
| + | És persze az integrálfüggvény "nagyon" folytonos, egészen pontosan Lipschitz-tuljadonságú vagy más névven Lipschitz-folytonos, azaz | ||
| + | :létezik olyan L nemnegatív szám, hogy minden x,y ∈ [a,b]-re | ||
| + | ::<math>|F(x) - F(y)| \leq L |x - y|\,</math> | ||
| + | azaz létezik olyan L, hogy minden x,y ∈ [a,b]-re | ||
:<math>\left|\int\limits_{a}^yf-\int\limits_{a}^x f\right|\leq L|y-x|\,</math> | :<math>\left|\int\limits_{a}^yf-\int\limits_{a}^x f\right|\leq L|y-x|\,</math> | ||
| − | + | Ugyanis a triviális felső becslésből: | |
:<math>\left|\int\limits_{a}^y f-\int\limits_{a}^x f\right|\leq \left|\int\limits_{x}^y f\right|\leq \int\limits_{x}^y|f|\leq \sup |f|\,|_{[x,y]}\cdot |y-x|\leq\sup |f|\cdot |y-x|</math> | :<math>\left|\int\limits_{a}^y f-\int\limits_{a}^x f\right|\leq \left|\int\limits_{x}^y f\right|\leq \int\limits_{x}^y|f|\leq \sup |f|\,|_{[x,y]}\cdot |y-x|\leq\sup |f|\cdot |y-x|</math> | ||
ahol L-nek alkalmas a sup |f| szám. | ahol L-nek alkalmas a sup |f| szám. | ||
| + | |||
| + | A Lipschitz-tulajdonság és folytonosság kapcsolatáról lásd még [itt]. | ||
| + | ====Példák==== | ||
| + | :<math>\left(\int\limits_{0}^x\mathrm{sc}\,t\,\mathrm{dt}\right)'(x)=?</math> | ||
| + | :<math>\left(\int\limits_{0}^{\sin x}\sqrt{1+t^3}\,\mathrm{d}t\right)'(x)=?</math> | ||
| + | Vizsgáljuk meg növekedés szempontjából az | ||
| + | :<math>[0,+\infty)\to \mathbf{R},\,x\mapsto \int\limits_{0}^x\frac{\sin t}{t}\,\mathrm{d}t</math> | ||
| + | szinusz integrálisz függvényt! | ||
==Primitívfüggvények== | ==Primitívfüggvények== | ||
| 160. sor: | 188. sor: | ||
<sub> Talán fellengzősség, de a fenti tételt néha az integrálszámítás alaptételének nevezik. Ennek egy kiterjesztett formája azonban tényleg méltó erre a névre: | <sub> Talán fellengzősség, de a fenti tételt néha az integrálszámítás alaptételének nevezik. Ennek egy kiterjesztett formája azonban tényleg méltó erre a névre: | ||
| − | '''Tétel.''' Ha az ''F'':[a,b]<math>\to</math> '''R''' differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és | + | '''Tétel.''' Ha az ''F'':[a,b]<math>\to</math> '''R''' differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és ''F'' Lipschitz-tulajdonságú, akkor ''F'' konstans. </sub> |
Az alábbi tétel szerint, amit szintén joggal neveznek a kalkulus fundamentális tételének, ha egy integrálható függvénynek van primitív függénye, akkor az integrálfüggvények és primitívfüggvények halmaza egybeesik, sőt: | Az alábbi tétel szerint, amit szintén joggal neveznek a kalkulus fundamentális tételének, ha egy integrálható függvénynek van primitív függénye, akkor az integrálfüggvények és primitívfüggvények halmaza egybeesik, sőt: | ||
| 167. sor: | 195. sor: | ||
:<math>\int\limits_{a}^bf(x)\,\mathrm{d}x=F(b)-F(a) \,</math> | :<math>\int\limits_{a}^bf(x)\,\mathrm{d}x=F(b)-F(a) \,</math> | ||
| − | + | Ez a kalkulus második fundamentális tétele. Érdemes alaposan megvizsgálni a feltételeit, mert tanulságos példákra lelhetünk. | |
| + | |||
| + | |||
++++++++++++++++++++++++++++++++++++++++++ | ++++++++++++++++++++++++++++++++++++++++++ | ||
+ létezik primitív függvénye + Dir | + létezik primitív függvénye + Dir | ||
| 205. sor: | 235. sor: | ||
Megjegyezük, hogy a görbe alatti területet nem véges összegekkel, hanem végtelen sorral közelítő Lebesgue-integrál olyan általános, hogy ilyen vagy még általánosabban definiált értelmeben nem integrálható függvényt keresni már komoly matematikai/halmazelméleti kihívást jelent. | Megjegyezük, hogy a görbe alatti területet nem véges összegekkel, hanem végtelen sorral közelítő Lebesgue-integrál olyan általános, hogy ilyen vagy még általánosabban definiált értelmeben nem integrálható függvényt keresni már komoly matematikai/halmazelméleti kihívást jelent. | ||
| + | ''A Newton--Leibniz-formula bizonyítása.'' Belátjuk, hogy a baloldal és a jobboldal abszolút eltérése minden pozitív számnál kisebb. Legyen ε > 0. Ekkor az integrálhatóság miatt létezik olyan δ > 0 szám, hogy '''minden''' η ∈ RF<sub>δ</sub>[a,b] Riamann-felosztásra | ||
| + | :<math>\left|\sum\limits_{i=1}^nf(\eta([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})-\int\limits_a^b f\right|< \varepsilon</math> | ||
| + | A bizonyítás trükkje az, hogy az F(b)-F(a) különbséget a közelító összegben lévő sok taggal, mint teleszkópikus összeggel tudjuk előállítani. Ugyanis a Lagrange-féle középértéktétel miatt egy tetszőlegesen rögzített η ∈ RF<sub>δ</sub>[a,b] felosztás minden részintervallumán létezik olyan ξ<sub>i</sub> ∈ [x<sub>i-1</sub>,x<sub>i</sub>], hogy | ||
| + | :<math>f(\xi_i)=F'(\xi_i)=\frac{F(x_i)-F(x_{i-1})}{x_i-x_{i-1}}</math> | ||
| + | Emiatt, ha azt az ξ felosztást választjuk, melynek osztópontjai az &eta osztópontjaival esenek egybe, de a részintervallumokból rendre a ξx<sub>i</sub> értékeket választja ki, akkor fennáll: | ||
| + | :<math> | ||
| + | \sum\limits_{i=1}^nf(\xi([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})=\sum\limits_{i=1}^n\frac{F(x_i)-F(x_{i-1})}{x_i-x_{i-1}}\cdot (x_i-x_{i-1})=\sum\limits_{i=1}^n F(x_i)-F(x_{i-1})=F(b)-F(a)\,</math> | ||
| + | Itt az összeg tagjai úgy esnek össze, ahogy azt a teleszkópikus összegeknél láthatjuk. Végül | ||
| + | :<math>\left|\sum\limits_{i=1}^nf(\eta([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})-\int\limits_a^b f\right|=\left|F(b)-F(a)-\int\limits_a^b f\right|< \varepsilon</math> | ||
| + | s mivel ε tetszőleges volt, ezért az egyenlőség fennáll. QED | ||
| + | |||
| + | Az ábrán van egy különlegesen fontos eset. Amikor az integrandus folytonos, akkor a fügvénynek biztosan létezik primitívfüggvénye. Ez annak a tételnek a duálisa, hogy folytonos függvény integrálható. | ||
| + | |||
| + | '''Tétel.''' ''f'' ∈ C[a,b], akkor ''f''-nek (biztosan) létezik primitívfüggvénye. | ||
| + | |||
| + | ''Ugyanis'' ekkor az integrálfüggvény minden pontban differenciálható, azaz az integrálfüggény primitívfüggvénye ''f''-nek. | ||
| + | |||
| + | '''Jelölés.''' Ha f folytonos, akkor indokolt a primitív függvények összességét a | ||
| + | :<math>\int f(x)\,\mathrm{d}x+C</math> | ||
| + | alakban írni, ahol C tetszőleges szám. | ||
| + | |||
| + | '''Megjegyzés.''' Ha tehát az a kérdés, hogy melyek a primitív függvényei f-nek, akkor a válasz a fenti kifejezés, ahol a '''határozatlan integrált''' szimbolizáló tag általában egy konkrét függvény. | ||
| + | |||
| + | ==Primitívfüggvény-keresés== | ||
| + | Primitívfüggvény-keresésnek két metódusa van. Az egyik a '''helyettesítéses integrálás''', a másik a '''parciális integrálás'''. Ezek előtt azonban egy triviális módszer, a deriválási táblázat megfodítása és az integrál eltolásinvarianciájának felhasználása. (Esetleg a lineáris argumentumú alapintegrál kiszámítása.) | ||
| + | |||
| + | ===Alapintegrálra visszavezethető integrálok=== | ||
| + | |||
| + | Ha tehát vesszük az elemi függvények és inverzeinek deriválási táblázatát, akkor jobbról balra olvasva megkapjuk az '''alapintegrálok''' táblázatát. | ||
| + | |||
| + | <table cellspacing=5> | ||
| + | <tr> | ||
| + | <td><math>\int x^n\,\mathrm{d}x</math> | ||
| + | <td><math>=\frac{x^{n+1}}{n+1}+C</math> | ||
| + | <td><math>(x\in\mathbb{R},n\in\mathbb{Z}\setminus\{-1\})</math> | ||
| + | <tr> | ||
| + | <td><math>\int x^\alpha\,\mathrm{d}x</math> | ||
| + | <td><math>=\frac{x^{\alpha+1}}{\alpha+1}+C</math> | ||
| + | <td><math>(x\in\mathbb{R}^+,-1\neq\alpha\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{x}\,\mathrm{d}x</math> | ||
| + | <td><math>=\,\ln|x|+C</math> | ||
| + | <td><math>(0\neq x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int e^x\,\mathrm{d}x</math> | ||
| + | <td><math>=\,e^x+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int a^x\,\mathrm{d}x</math> | ||
| + | <td><math>=\frac{a^x}{\ln a}+C</math> | ||
| + | <td><math>(x\in\mathbb{R},1\neq a\in\mathbb{R}^+)</math> | ||
| + | <tr> | ||
| + | <td><math>\int\sin x\,\mathrm{d}x</math> | ||
| + | <td><math>=-\cos x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\cos x\,\mathrm{d}x</math> | ||
| + | <td><math>=\sin x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\sin^2x}\,\mathrm{d}x</math> | ||
| + | <td><math>=-\mathrm{ctg}\,x\,+C</math> | ||
| + | <td><math>(k\pi\neq x\in\mathbb{R},k\in\mathbb{Z})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\cos^2x}\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{tg}\,x\,+C</math> | ||
| + | <td><math>(\frac{k\pi}{2}\neq x\in\mathbb{R},k\in\mathbb{Z})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\mathrm{sh}\, x\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{ch}\,x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\mathrm{ch}\, x\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{sh}\, x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\mathrm{sh}^2x}\,\mathrm{d}x</math> | ||
| + | <td><math>=-\mathrm{cth}\, x\,+C</math> | ||
| + | <td><math>(0\neq x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\mathrm{ch}^2x}\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{th}\, x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{1+x^2}\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{arc\,tg}\, x\,+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{1-x^2}\,\mathrm{d}x</math> | ||
| + | <td><math>=\frac{1}{2}\ln\left|\frac{x+1}{x-1}\right|+C</math> | ||
| + | <td><math>=\left\{{\mathrm{ar\,th}\,x+C\quad(1>|x|\in\mathbb{R})\atop\mathrm{ar\,ch}\,x+C\quad(1<|x|\in\mathbb{R})}\right.</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\sqrt{1-x^2}}\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{arc\,sin} x\,+C</math> | ||
| + | <td><math>(1>|x|\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\sqrt{1+x^2}}\,\mathrm{d}x</math> | ||
| + | <td><math>=\mathrm{ar\,sh}\,x+C</math> | ||
| + | <td><math>(x\in\mathbb{R})</math> | ||
| + | <tr> | ||
| + | <td><math>\int\frac{1}{\sqrt{x^2-1}}\,\mathrm{d}x</math> | ||
| + | <td><math>=\ln\left|x+\sqrt{x^2-1}\right|+C</math> | ||
| + | <td><math>=\left\{\;{\mathrm{ar\,ch}\,x+C\quad\quad(1<x\in\mathbb{R})\atop\!-\mathrm{ar\,ch}(-x)+C\quad(1>x\in\mathbb{R})}\right.</math> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | ====Alapintegrálok kiszámítása táblázatból==== | ||
| + | :<math> | ||
| + | \int\frac{1}{\cos^2x}\,\mathrm{d}x=\mathrm{tg}\,x+C\,</math> | ||
| + | vagy a legkönnyebben elronthatók: | ||
| + | |||
| + | :<math> | ||
| + | \int 5 \,\mathrm{d}x=5x+C\,</math> | ||
| + | |||
| + | :<math> | ||
| + | \int 0\, \mathrm{d}x=C\,</math> | ||
| + | ====Alapintegrálok és eltolásinvariancia==== | ||
| + | Az integrál '''eltolásinvarianciáját''' használva: | ||
| + | :<math> | ||
| + | \int\frac{1}{x+8}\,\mathrm{d}x=\mathrm{ln}\,|x+8|+C\,</math> | ||
| + | ====Lineáris agrumentumú integrandus==== | ||
| + | |||
| + | A '''lineáris agrumentumúkra''' vonatkozó képlet: | ||
| + | :<math> | ||
| + | \int f(ax+b)\,\mathrm{d}x=\frac{1}{a}F(ax+b)+C\,</math> | ||
| + | ahol F'=f. Hiszen az összetett függvény deriválási szabálya szerint: | ||
| + | :<math>\left(\frac{1}{a}F(ax+b)\right)'=\frac{1}{a}F'(ax+b)=\frac{1}{a}\cdot f(ax+b)\cdot a= f(ax+b)</math> | ||
| + | Ezzel pl: | ||
| + | :<math> | ||
| + | \int\sin(5x-7)\,\mathrm{d}x=-\frac{1}{5}\cos(5x-7)+C\,</math> | ||
| + | '''Megjegyzés.''' Érdemes fejünkbe vésni a sin függvény deriváltajainak függvénysorozatát: | ||
| + | :<math>\sin</math> | ||
| + | :<math>\cos</math> | ||
| + | :<math>-\sin</math> | ||
| + | :<math>-\cos</math> | ||
| + | :<math>\sin</math> | ||
| + | :<math>\cos</math> | ||
| + | :<math>\vdots</math> | ||
| + | felfejé haladva integrálunk, lefelé haladva deriválunk. | ||
| + | |||
| + | pl. | ||
| + | :<math> | ||
| + | \int e^{(2008x-2007)}\,\mathrm{d}x=\frac{1}{2008}e^{(2008x-2007)}+C\,</math> | ||
| + | ====Polinom/lineáris alak==== | ||
| + | |||
| + | :<math>\int\frac{x-3}{x+1}\,\mathrm{d}x=\int\frac{x+1-4}{x+1}\,\mathrm{d}x=\int 1-\frac{4}{x+1}\,\mathrm{d}x=x-4\,\mathrm{ln}\,|x+1|+C</math> | ||
| + | |||
| + | :<math>\int\frac{2x+1}{x+2}\,\mathrm{d}x=\int\frac{2(x+2)-3}{x+2}\,\mathrm{d}x=\int 2-\frac{3}{x+2}\,\mathrm{d}x=2x-3\,\mathrm{ln}\,|x+2|+C</math> | ||
| + | |||
| + | :<math>\int\frac{x^2+2}{x-1}\,\mathrm{d}x=?</math> | ||
| + | itt már érdemes polinomosztással eljárni: | ||
| + | (x^2 + 2) : (x - 1) = x + 1 | ||
| + | - x^2 - x | ||
| + | --------- | ||
| + | x + 2 | ||
| + | - x - 1 | ||
| + | -------- | ||
| + | 3 | ||
| + | :<math>\int\frac{x^2+2}{x-1}\,\mathrm{d}x=\int x+1+\frac{3}{x-1}\,\mathrm{d}x=\frac{x^2}{2}+x+3\,\mathrm{ln}\,|x-1|+C</math> | ||
| + | |||
| + | Néha x<sup>2</sup> + 1 nevezőjűre is működik: | ||
| + | |||
| + | :<math>\int\frac{x^2-7}{x^2+1}\,\mathrm{d}x=\int \frac{x^2+1-8}{x^2+1}\,\mathrm{d}x=\int 1-\frac{8}{x^2+1}\,\mathrm{d}x=x-8\,\mathrm{arc\,tg}\,x+C</math> | ||
| + | |||
| + | ====Linearizáló formulák==== | ||
| + | Ezek arra alkalmasak, hogy a sin<sup>2</sup>, cos<sup>2</sup>, sh<sup>2</sup>. ch<sup>2</sup> függvényeket (illetve alkalmasan megváltoztatott argumentumú változatukat) ki lehessen integrálni: | ||
| + | :<math> | ||
| + | \sin^2 x=\frac{1-\cos(2x)}{2}\,</math> | ||
| + | :<math> | ||
| + | \cos^2 x=\frac{1+\cos(2x)}{2}\,</math> | ||
| + | :<math> | ||
| + | \mathrm{sh}^2 x=\frac{\mathrm{ch}(2x)-1}{2}\,</math> | ||
| + | :<math> | ||
| + | \mathrm{ch}^2 x=\frac{\mathrm{ch}(2x)+1}{2}\,</math> | ||
| + | Mindezek a következők miatt állnak fenn: | ||
| + | |||
| + | :<math>\cos^2+\sin^2=1\,</math> | ||
| + | :<math>\cos^2-\sin^2=\cos(2x)\,</math> | ||
| + | ezért ezeket kivonva ill. összeadva, majd 2-vel elosztva a felső kettőt kapjuk. A másik kettő: | ||
| + | :<math>\mathrm{ch}^2-\mathrm{sh}^2=1\,</math> | ||
| + | :<math>\mathrm{ch}^2+\mathrm{sh}^2=\mathrm{ch}(2x)\,</math> | ||
| + | Itt érdemes megjegyezni az '''Osborne-szabályt''': ha egy trigonometrikus azonosságban kicseréljük a megfelelő hiperbolikus függvényekre az összetevőket és minden olyan tag előjelét megváltoztatjuk, melyek két sh szorzatából állnak (speciálisan a sh<sup>2</sup>-ek elé egy - jelet teszünk), akkor megkapjuk a hiperbolikus azonosságot. Lásd: [http://mathworld.wolfram.com/OsbornesRule.html ''Osborne-szabály'']. | ||
| + | |||
| + | Ezek főleg határozott integráloknál adnak "szép" eredményt | ||
| + | |||
| + | '''Példa.''' | ||
| + | :<math>\int\limits_{0}^{\pi}\sin^2 x\mathrm{d}x=\int\limits_{0}^{\pi}\frac{1-\cos(2x)}{2}\mathrm{d}x=\left[\frac{1}{2}x-\frac{1}{4}\sin(2x)\right]_0^\pi=\frac{\pi}{2}</math> | ||
| + | |||
| + | ===Helyettesítéses integrálás=== | ||
| + | |||
| + | Az első keresési eljárás az összetett függvény deriválási szabályának megfordításán alapul. | ||
| + | |||
| + | '''Tétel.''' Legyen g:I <math>\to</math> J, F: J <math>\to</math> '''R''' folytonosan differenciálható függvények és f: J <math>\to</math> '''R''' pedig olyan, hogy az F' = f, akkor az x <math>\mapsto</math> f(g(x)) <math>\cdot</math> g'(x)-nek is létezik primitív függvénye és | ||
| + | :<math>\int f(g(x))\cdot g'(x)\,\mathrm{d}x= F(g(x))+C\,</math> | ||
| + | |||
| + | ''Bizonyítás.'' A primitív függvény létezését az garantálja, hogy az integrandus folytonos. | ||
| + | |||
| + | Elegendő ellenőrizni, hogy x <math>\mapsto</math> F(g(x)) primitív függvénye x <math>\mapsto</math> f(g(x)) <math>\cdot</math> g'(x)-nek, azaz az előbbi deriváltja az utóbbi: | ||
| + | :<math>F(g(x))'=F'(g(x))\cdot g'(x)=f(g(x))\cdot g'(x)</math> | ||
| + | QED. | ||
| + | ====...-alakú integrálok==== | ||
| + | Ebből a tételből származtathatjuk a "'''... alakú integrál'''okat": | ||
| + | |||
| + | # <math>\int f(ax+b)\,\mathrm{d}x= \frac{1}{a}F(ax+b)+C\,\quad\quad(\;g(x)=ax+b\;\mathrm{esete})</math> | ||
| + | # <math>\int g^n(x)\cdot g'(x)\,\mathrm{d}x= \frac{g^{n+1}(x)}{n+1}+C\,\quad\quad(\;f(\,.\,)=(\,.\,)^n\;\mathrm{esete}\;n\ne -1)</math> | ||
| + | # <math>\int \frac{g'(x)}{g(x)}\,\mathrm{d}x= \mathrm{ln}|g(x)|+C\,\quad\quad(\;f(\,.\,)=\mathrm{ln}(\,.\,)\;\mathrm{esete}\;)</math> | ||
| + | |||
| + | '''Példák.''' | ||
| + | |||
| + | '''1.'''<math> \int\frac{x}{\cos^2 (x^2+5)},\mathrm{d}x=\frac{1}{2}\int\frac{2x}{\cos^2 (x^2+5)},\mathrm{d}x=\frac{1}{2}\cdot\mathrm{tg}\,(x^2+5)+C</math> | ||
| + | hiszen a "külső" függvény: | ||
| + | :<math>f(\,.\,)=\frac{1}{\cos^2(\,.\,)} \quad\quad\to_{\int}\quad\quad F(\,.\,)=\mathrm{tg}\,(\,.\,) </math> | ||
| + | a "belső" függvény: | ||
| + | :<math>g(x)=x^2+5 \quad\quad\to'\quad\quad g'(x)=2x </math> | ||
| + | |||
| + | '''2.''' | ||
| + | :<math> \int\frac{\mathrm{arc\,tg}\,x}{x^2+1}\,\mathrm{d}x= \int(\mathrm{arc\,tg}\,x)^1\cdot\frac{1}{x^2+1}\,\mathrm{d}x=\frac{\mathrm{arc\,tg}^2\,x}{2}+C</math> | ||
| + | hiszen a "külső" függvény: | ||
| + | :<math>f(\,.\,)=(\,.\,)^1 \quad\quad\to_{\int}\quad\quad F(\,.\,)=\frac{(\,.\,)^2}{2}</math> | ||
| + | a "belső" függvény: | ||
| + | :<math>g(x)=\mathrm{arc\,tg}\,x \quad\quad\to'\quad\quad g'(x)=\frac{1}{x^2+1} </math> | ||
| + | |||
| + | '''3.''' | ||
| + | :<math> \int\frac{1}{(\mathrm{arc\,sin}\,x)\sqrt{1-x^2}}\,\mathrm{d}x= \int\frac{\frac{1}{\sqrt{1-x^2}}}{\mathrm{arc\,sin}\,x}\,\mathrm{d}x=\mathrm{ln}\,|\mathrm{arc\,sin}\,x|+C</math> | ||
| + | hiszen a "külső" függvény: | ||
| + | :<math>f(\,.\,)=(\,.\,)^{-1} \quad\quad\to_{\int}\quad\quad F(\,.\,)=\mathrm{ln}\,|\,.\,|</math> | ||
| + | a "belső" függvény: | ||
| + | :<math>g(x)=\mathrm{arc\,sin}\,x \quad\quad\to'\quad\quad g'(x)=\frac{1}{\sqrt{1-x^2}} </math> | ||
| + | |||
| + | '''4.''' | ||
| + | :<math> \int x^2\sqrt[2008]{\mathrm{sh}\,x^3}\cdot \mathrm{ch}\,(x^3)\,\mathrm{d}x= \frac{1}{3}\int \sqrt[2008]{\mathrm{sh}\,x^3}\cdot (3x^2\mathrm{ch}\,(x^3))\,\mathrm{d}x=\frac{2008}{3\cdot 2009}(\mathrm{sh}\,x^3)^{\frac{2009}{2008}}+C</math> | ||
| + | hiszen a "külső" függvény: | ||
| + | :<math>f(\,.\,)=(\,.\,)^{\frac{1}{2008}} \quad\quad\to_{\int}\quad\quad F(\,.\,)=\frac{2008}{2009}(\,.\,)^{\frac{2009}{2008}}</math> | ||
| + | a "belső" függvény: | ||
| + | :<math>g(x)=\mathrm{sh}\,(x^3) \quad\quad\to'\quad\quad g'(x)=3x^2\mathrm{ch}\,(x^3) </math> | ||
| + | |||
| + | ====Integrálás a helyettesítés elvégzésével==== | ||
| + | '''Megjegyzés.''' Intermezzóként megemlítjük, hogy a helyettesítés elnevezés abból fakad, hogy ekkor lényegében új ismeretlent vezetünk be. Persze az ezzel való számolás egy egészen más szemléletet igényel. A fő képlet ekkor: | ||
| + | :<math> | ||
| + | \int g(x)\,\mathrm{d}x=\left.\int f(u)\,\mathrm{d}u\right|_{u=u(x)}= F(u)+C|_{u=u(x)}</math> | ||
| + | ahol el kell végezni az | ||
| + | :<math>u=u(x)\quad\quad\to^{(\,.\,)^{-1}}\quad\quad x=x(u)\,</math> | ||
| + | :<math>\frac{\mathrm{d}u}{\mathrm{d}x}=u'(x)\,\quad\quad\to\quad\quad \mathrm{d}x=\frac{\mathrm{d}u}{u'(x(u))}</math> | ||
| + | szimbolikus helyettesítést. | ||
| + | |||
| + | '''5.''' (exponenciális helyettesítés) | ||
| + | |||
| + | :<math>\int \frac{e^x}{1+e^{2x}}\,\mathrm{d}x=?</math> | ||
| + | |||
| + | :<math>u=e^x\quad\quad\to^{(\,.\,)^{-1}}\quad\quad x=\mathrm{ln}\,u</math> | ||
| + | :<math>\frac{\mathrm{d}u}{\mathrm{d}x}=e^x=u\quad\quad\to\quad\quad \mathrm{d}x=\frac{\mathrm{d}u}{u}</math> | ||
| + | |||
| + | :<math> \int \frac{e^x}{1+e^{2x}}\,\mathrm{d}x=\left.\int \frac{\,^1\!\!\not{\!u}\,}{1+u^2}\cdot\frac{1}{\not{\!u}_1}\,\mathrm{d}u\right|_{u=e^x}=\left.\mathrm{arc\,tg}\,(u) +C\right|_{u=e^x}=\mathrm{arc\,tg}\,(e^x) +C</math> | ||
| + | |||
| + | |||
| + | '''5.''' (gyökös helyettesítés) | ||
| + | |||
| + | :<math>\int \frac{2x}{1+\sqrt{x}}\,\mathrm{d}x=?</math> | ||
| + | |||
| + | :<math>u=\sqrt{x}\quad\quad\to^{(\,.\,)^{-1}}\quad\quad x=u^2</math> | ||
| + | :<math>\frac{\mathrm{d}u}{\mathrm{d}x}=\frac{1}{2\sqrt{x}}=\frac{1}{2u}\quad\quad\to\quad\quad \mathrm{d}x=2u\,\mathrm{d}u</math> | ||
| + | |||
| + | :<math> \int \frac{2x}{1+\sqrt{x}}\,\mathrm{d}x=\int \frac{2u^2}{1+u}\,\frac{1}{2u}\mathrm{d}u\,\mathrm{d}u=\int \frac{u}{1+u}\,\mathrm{d}u=</math> | ||
| + | |||
| + | :<math>\int \frac{u+1-1}{1+u}\,\mathrm{d}u= \int 1-\frac{1}{1+u}\,\mathrm{d}u=\left. u-\mathrm{ln}\,|1+u|+C\right|_{u=\sqrt{x}}=\sqrt{x}-\mathrm{ln}\,\sqrt{x}+C</math> | ||
| + | |||
| + | '''6.''' (trigonometrikus helyettesítés) | ||
| + | |||
| + | :<math>\int \sqrt{1-x^2}\,\mathrm{d}x=?</math> | ||
| + | |||
| + | :<math>u=\mathrm{arc\,cos}\,x\quad\quad\to^{(\,.\,)^{-1}}\quad\quad x=\cos u</math> | ||
| + | :<math>\frac{\mathrm{d}u}{\mathrm{d}x}=-\frac{1}{\sqrt{1-x^2}}=-\sin u\quad\quad\to\quad\quad \mathrm{d}x=-\sin u\,\mathrm{d}u</math> | ||
| + | |||
| + | :<math>\int \sqrt{1-x^2}\,\mathrm{d}x=\int \sqrt{1-\cos^2x}\,(-\sin u)\mathrm{d}u=-\int \sin^2u\,\mathrm{d}u=</math> | ||
| + | |||
| + | :<math>-\int \frac{1-\cos(2u)}{2}\,\mathrm{d}u=\left.-\frac{1}{2}u+\frac{1}{4}\sin(2u)+C\right|_{u=\mathrm{arc\,cos}\,x}=-\frac{1}{2}\mathrm{arc\,cos}\,x+\frac{1}{4}\sin(2\mathrm{arc\,cos}\,x)+C</math> | ||
| + | ===Parciális integrálás=== | ||
| + | A helyettesításes integrálás a függvénykompozíció deriválására szolgáló képlet felhasználása volt primitívfüggvény keresésre. Most a szorzási szabályt fogjuk használni. | ||
| + | |||
| + | '''Tétel.''' Legyen f,g:[a,b] <math> \to</math> '''R''' folytonos és F,G:[a,b] <math> \to</math> '''R''' differenciálható olyan, hogy F' = f, G' = g. Ekkor az alábbi képletben szereplő összes integrandusnak létezik primitív függvénye és | ||
| + | :<math>\int Fg=FG - \int fG\,</math> | ||
| + | |||
| + | ''Bizonyítás.'' Elég a bizonyítani, hogy a jobb oldal deriváltja a baloldali integrandus. Ehelyett egy kicsit másként csináljuk: belátjuk, hogy az FG függvény primitívfüggvénye az fG + Fg függvénynek, majd kefejezzük velőle a fenti formula baloldalát: | ||
| + | :<math>(FG)'=F'G+FG'=fG+Fg\,</math> | ||
| + | tehát | ||
| + | :<math>FG=\int fG+Fg=\int fG+\int Fg\,</math> | ||
| + | amiből már következik a fenti formula. QED. | ||
| + | ====Polinom szor exp, trig, hip ==== | ||
| + | Az első alkalmazás az, amikor a egymás után parciális integrálásokkal polinommentes formulává alakítjuk az integrandust. Ekkor a fenti képlet F-je a polinom, amiből egyel alacsonyabb fokú polinomszoros integrandus keletkezik az ∫fG integrál esetén. | ||
| + | |||
| + | :<math> | ||
| + | \int x\sin x\,\mathrm{d}x=x(-\cos x)-\int 1\cdot (-\cos x)\,\mathrm{d}x=-x\cos x + \sin x+C</math> | ||
| + | Hiszen | ||
| + | :<math>F = \mathrm{id} \quad\quad\to '\quad\quad f=F'=1</math> | ||
| + | :<math>g = \mathrm{sin} \quad\quad\to ^\int\quad\quad G=\int g=-\cos</math> | ||
| + | |||
| + | Egy hasonló: | ||
| + | :<math> | ||
| + | \int (2x+1)\mathrm{sh}\,(3x-2)\,\mathrm{d}x=(2x+1)\frac{1}{3}\mathrm{ch}\,(3x-2)-\int 2\cdot \frac{1}{3}\mathrm{ch}\,(3x-2)\,\mathrm{d}x=</math> | ||
| + | |||
| + | :<math>=\frac{2x+1}{3}\mathrm{ch}\,(3x-2)-\frac{2}{9}\mathrm{sh}\,(3x-2)</math> | ||
| + | Hiszen | ||
| + | :<math>F = 2\mathrm{id}+1 \quad\quad\to '\quad\quad f=F'=2</math> | ||
| + | :<math>g = \mathrm{sh}\circ(3\mathrm{id}-2) \quad\quad\to ^\int\quad\quad G=\int g=\frac{1}{3}\mathrm{ch}\circ(3\mathrm{id}-2) </math> | ||
| + | ====Rekurziós integrálok, formulák==== | ||
| + | '''1.''' | ||
| + | : <math>\int\frac{\mathrm{ln}\,x}{x}\mathrm{d}x=\mathrm{ln}^\,x-\int \frac{1}{x}\cdot\mathrm{ln}\,x \,\mathrm{d}x</math> | ||
| + | az | ||
| + | :<math>F = \mathrm{ln} \quad\quad\to '\quad\quad f=F'=\frac{1}{\mathrm{id}}</math> | ||
| + | :<math>g = \frac{1}{\mathrm{id}} \quad\quad\to ^\int\quad\quad G=\int g= \mathrm{ln}</math> | ||
| + | szereposztással. A formulában visszatért a keresett integrál, így ezt kifejezve: | ||
| + | : <math>\int\frac{\mathrm{ln}\,x}{x}\,\mathrm{d}x=\frac{1}{2}\mathrm{ln}^\,x+C</math> | ||
| + | '''2.''' | ||
| + | :<math>\int\cos(x)\cdot e^x\,\mathrm{d}x=\cos(x)\cdot e^x -\int(-\sin x)\cdot e^x\,\mathrm{d}x=\cos(x)\cdot e^x+\sin(x)\cdot e^x-\int\cos(x)\cdot e^x\,\mathrm{d}x</math> | ||
| + | amiből | ||
| + | :<math>\int\cos(x)\cdot e^x\,\mathrm{d}x=\frac{1}{2}(\cos(x)\cdot e^x +\sin(x)\cdot e^x)+C=</math> | ||
| + | tehát kétszeri parciális integrálással értük el. | ||
| + | '''3.''' Rekurziós formulát kapunk az alábbi <math>I_n</math> alakú integrálokra: | ||
| + | <math>I_n=\int\frac{1}{(x^2+1)^n}\,\mathrm{d}x=\int\frac{x^2+1}{(x^2+1)^n}-\frac{x^2}{(x^2+1)^n}\,\mathrm{d}x=\int\frac{1}{(x^2+1)^{n-1}}-\frac{x^2}{(x^2+1)^n}\,\mathrm{d}x</math> | ||
| + | az utolsó tagot parciálisan integráljuk ki: | ||
| + | |||
| + | :<math>=\frac{1}{2}\int x\frac{2x}{(x^2+1)^n}\,\mathrm{d}x=\frac{1}{2}\cdot \frac{x}{(n-1)(x^2+1)^{n-1}}-\int\frac{1}{(n-1)(x^2+1)^{n-1}}\,\mathrm{d}x=\frac{1}{2}\cdot \frac{x}{(n-1)(x^2+1)^{n-1}}-\frac{1}{n-1}\cdot I_{n-1}</math> | ||
| + | azaz <math> I_n</math> kifejezhető <math>I_{n-1}</math>-segítségével. | ||
| + | ====Inverzfüggvények integrálja==== | ||
| + | Az | ||
| + | :<math>\int f^{-1}=\int f^{-1}\cdot 1=f^{-1}\cdot \mathrm{id}-\int \mathrm{id}\cdot (f^{-1})'</math> | ||
| + | trükk sokszor alkalmas arra, hogy az inverz függvények integrálját parciálisan kiintegráljuk, hiszen az inverz függvények deriváltjának képlete az utolsó tényezőt a kezünkre játssza. Speciálisan a módszer alkalmas az összes ln, arc és ar függvény kiintegrálására. | ||
| + | |||
| + | '''1.''' | ||
| + | :<math>\int\mathrm{arc\,sin}\,(x)\,\mathrm{d}x=\int\mathrm{arc\,sin}\,(x)\cdot 1\,\mathrm{d}x=x\cdot \mathrm{arc\,sin}\,(x)-\int x\frac{1}{\sqrt{1-x^2}}\,\mathrm{d}x=</math> | ||
| + | :<math>=x\cdot \mathrm{arc\,sin}\,(x)+\frac{1}{2}\int \frac{-2x}{\sqrt{1-x^2}}\,\mathrm{d}x=x\cdot \mathrm{arc\,sin}\,(x)+\sqrt{1-x^2}+C</math> | ||
[[Kategória:Matematika A1]] | [[Kategória:Matematika A1]] | ||
A lap jelenlegi, 2009. április 29., 12:31-kori változata
Tartalomjegyzék
|
Határozott integrál
Az egyváltozós analízis történetileg kialakult két jellegzetes témaköre közül az egyik az érintőproléma (lényegében a differenciálelmélet) a másik a területszámítás problémája, vagy régies elnevezéssel a kvadratúra-feldat (ami lényegében az integrálelmélet). Most a kvadratúra, azaz a függvénygörbe alatti terület definícióját adjuk meg. Ehhez azonban néhény segédfogalmat kell megismernünk.
Az [a,b] korlátos és zárt intervallum egy Riemann-felosztásán nem mást értünk mint egy olyan kiválasztófüggvényt, mely az [a,b]-t unióként előállító, egymásba nem nyúló intervallumokból álló halmaz minden egyes eleméhez egy az adott elemben lévő elemet rendel, azaz egy olyan
függvényt, melyre:
- n olyan véges természetes szám, hogy x0 = a < x1 < x2 < ... < xn = b és
- minden J ∈ Dom(η) esetén
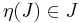 .
.
Az [a,b] összes Riemann-felosztásai halmazát RF[a,b] jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes részintervallum hossza kisebb egy δ > 0 pozitív számnál, azt RFδ[a,b] jelöli, azt a halmazt az [a,b] összes δ-nál finomabb Riemann-felosztásának nevezük.
Egy f, az [a,b]-n értelmezett függvény egy Riemann-közelítő összegén a
ahol η a fenti jelölésekkel az [a,b] egy Riemann-felosztása.
Ekkor már definiálhatjuk az integrálhatóságot:
Definíció. Legyen f:[a,b]  Regy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az I valós szám, ha
Regy zárt és korlátos intervallumon értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az I valós szám, ha
Belátható, hogy ha f integrálható, akkor I egyértelmű és ekkor ennek a számnak a jelölésére az
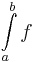 , vagy az
, vagy az 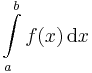
szimbólum szolgál.
Az [a,b] intervallumon Riemann-integrálható függvények halmazát R[a,b] jelöli.
Az integrál lényegében a függvénygörbe alatti terület. Integrálható függvény esetén létezik ez a terület, azaz a Riemann-felosztást egyre finomabbra véve, a Riemann-közelítő összeg minden előre megadott legnagyobb ε eltérésnél közelebb kerül I-hez.
Világos, hogy ha egy függvény integrálható, akkor minden részintervallumán is integrálható (hisz ekkor azokat a felosztásokat kell venni, amik a részintervallumon belül is felosztások, és persze ezek szerint is képezve a határátmenetet, létező határértéket kapunk). Minhogy az integrál egy szám, integrálható f esetén értelmes ha definiáljuk a következő, úgy nevezett integrálfüggvényt (vagy a-ban eltűnő integrálfüggvényt):
Definíció szerinti példák
1. Példa. Jóformán az egyetlen függvény, aminek az integrálhatóságát a definíció alapján könnyen igazolni tudjuk, az a konstans függvény. Az f(x) = c esetén a kiválaszott pontok mindig c függvényértékűek, és az összes közelítő összeg mindig
azaz
Már ezzel is azonban fel tudunk írni egy integrálfüggvényt: f:[a,b] R, f ≡ c esetén:
R, f ≡ c esetén:
2. Példa. Nem minden függvény integrálható.
2. a. Zárjuk le a reciprok függvényt egy ponttal:
(Riemann az 1854-es habilitációs dolgozatában definiálta és vizsgálta a most Riemann-integrálhatóságnak nevezett fogalmaz, mindazonáltal az integrál első, a szigorúság követelményének eleget tévő definícióját Cauchy adta (1821) az intuitívet pedig Leibniz.) Ez a függvény nem integrálható, mert akármilyen fimon intervallumfelosztás esetén, ha az első intervallumot δ hosszúra választjuk, definiálható egy η([x0,x1]) < δ2 érték, azaz f(η([x0,x1])) > 1/ δ2. Ekkor viszont az első téglalap területe 1/δ lesz, ami δ \to 0 esetén a +∞-be tart, azaz az összterület nem lesz véges.
2. b. Legyen f a Dirichlet-függvény:
ahol Q a racionális számok halmaza, R / Q pedig nyilván az irracionális. Ez a függvény nem Riemann-integrálható, bár korlátos, mert akármilyen finom intervallum-felbontás esetén van egy olyan Riemann-kiválasztó függvény, mely mindig racionális pontokat választ ki és ezáltal a közelítő összeg mindig 1 és olyan, mely mindig irracionálist, azaz ezzel a közelítő összeg 0. Mindig lesz tehát két olyan felbontás, mely összegek különbsége legalább 1.
A Riemann-inregrálhatóság szükséges és elégséges feltétele
Bár a Riemann-integrálhatóság általában könnyen kezeéhető fogalom, a következő tétel bizonyításához azonban az egyváltozós analízis szinte összes eszközét be kell vetni. Nem csoda, hogy csak 1905-ben fogalmazhatta meg Lebesgue, egy tágabb perspektívából szemlélve a Riemann-integrált.
Tétel. Legyen f: [a,b]  R korlátos és zárt intervallumon értelmezett függvény. f pontosan akkor integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
R korlátos és zárt intervallumon értelmezett függvény. f pontosan akkor integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
Itt Lebesgue-nullmértékűnek nevezünk egy H ⊆ R halmazt, ha minden ε > 0-hoz létezik olyan (In) intervallumsorozat, hogy ennek összhossza < ε és lefedi H-t.
Biztos nem nullmértékű például egy nemelfajuló intervallum, mert annak a mértéke az intervallum nemnulla hossza. De véges halmaz nullmértékű, mert lefedhető, egy határértékben eltűnő intervallumsorozat-rendszerrel. Belátható, hogy megszámlálható pont nullmértékű halmazt alkot. Konkrétan, könyen belátható, hogy az 1/n pontjai nullmértékű halmazt alkotnak.
Világos, hogy a Dirichlet-függvényes példa azért jó ellenpélda, mert ez a függvény [0,1]-en mindenhol szakad, azaz discon(Dir)=[0,1], melynek a mértéke 1.
Példa. Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. A konstrukció e következő. Először definiáljuk az ördög lépcsője függvényt:
A [0,1] intervallumot osszuk 3 részre és vegyük ki a belső nyílt harmadot. Ezen a szakaszon legyen a függvény értéke 1/2. Ismételjük a megmaradt két zárt intervallumra, és az érték legyen ott 1/4 ill. 3/4. A fennmaradt részeket is osszuk, majd a középső harmad értéke mindig a két szélső közepe legyen... Ha csak a belső harmadokat vesszük, akkor ami megmarad a halmazból, az az úgy nevezett Cantor-halmaz. A Cantor-halmaz kontinuum számosságúan végtelen, de Lebesgue-nullmértékű -- ezt a két dolgot persze nem bizonyítjuk. A függvény mindenhol folytonos, a m.m- deriválható és a deriváltja 0 (de nem intervallumon értelmezett: Dom = [0,1]\C). Ha most vesszük a deriváltfüggvényét és kiterjesztjük a C pontjaiban úgy, hogy ott 1 legyen az értéke, akkor ez egy kontinuum számosságú, de Lebesgue-nullmértékű halmazon szakadó, korlátos függvény, azaz integrálható. És az integrálja 0. Ebből is látható, hogy a fenti ekvivalenciatétel csodálatosan oldja meg, hogy bár a Riemann-felosztás véges, kontinuum számosságú, L-0-m. résszel is el tud bánni.
A Riemann-integrálhatóság néhány kritériuma
Részletezünk néhány hasznos esetet a fenti tételből.
-
![f\in \mathrm{R}[a,b]\;\Rightarrow\;f\in \mathrm{B}[a,b]](/upload/math/b/8/3/b83309f476aa7945359baebf79f1e9b7.png)
- csak korlátos függvények R-intgrálhatóak
-
![f\in \mathrm{R}[a,b]\;\Leftarrow\;f\in \mathrm{C}[a,b]](/upload/math/6/1/b/61b955edf5d07d91ba8d85640fc49029.png)
- (Cauchy) világos: ha folytonos, akkor nincs szakadási pontja, és korlátos a Weierstrass-tétel miatt
-
![f\in \mathrm{R}[a,b]\;\Leftarrow\;f\in \mathrm{M}[a,b]](/upload/math/f/0/3/f03e7b5351b87da25a7c01f433aa9c8d.png)
- monoton függvény R-integrálható (minden feltétel nélkül), amiatt a nem említett tétel miatt, hogy intervallumon értelmezett, monoton függvénynek csak megszámlálható szakadási pontja van, korlátos és zárt intervallumon pedig egy ilyen függvény korlátos.
Feladat. Intergálhatóak-e az alábbi függvények és ha igen, mi az integráljuk?
1.
Igen, mert folytonos (illetve legfeljebb csak 1 ponton szakad, miközben korlátos). Ezen kívül páratlan: |-x|sin(1/-x) = -|x|sin(1/x), emiatt az origóra szimmetrikus intervallumon az integrálja:
2.
Igen, mert monoton. Az integrálját elegendő egyetlen végtelenül finomodó felosztássorozathoz tartozó közelítő összegsorozat határértékeként számolni, hiszen ha ez nem konvergálna, akkor nem teljesülne a definícióban megkövetelt határérték létezése. Az intervallumot 2m részre osztjuk fel. Ekkor az összeg:
Ennek a határértéke a mértani sor összegképlete miatt:
3.
Megszámlálható sok szakadása van ugyan a függvénynek, de nem korlátosan a szakadások, így a függvény nem integrálható:
Az határozott integrál néhány tulajdonsága
A következőkben feltesszük, hogy az f és g a formulákban szereplő intervallumokat tartalmazó valamely intervallumon Riemann-integrálható.
- Intervallum szerinti additivitás:
- Integrandus szerinti additivitás:
- Integrandus szerinti monotonitás.
- Integrandus szerinti homogenitás:
- Abszolút becslés.
-
- Triviális alsó és felső becslés.
-
- Eltolásinvariancia.
Az integrálfüggvény néhány tulajdonsága
Az integrálfüggvény viselkedését vizsgálva meglepő következtetésre juthatunk.
Példa. Vegyük az alábbi lépcsős függvényt:
írjuk fel az integrálfüggvényét tudva-tudván, hogy az nem más mint a területfüggvény:
Ábrázolva, azt kapjuk, hogy T képe egy törött vonal, folytonos és mindehol, ahol nem törik, a deriváltja az integrandus. T diff.-ható a [0,1)U(1,2] halmazon és
Az integrálfüggvény differenciálhatóságáról
Az integrandus folytonossági helyein az integrálfüggvény valóban differenciálható. Az alábbi tételt az analízis első alaptételének szokás nevezni.
Tétel. -- A kalkulus fundamentális tétele I. -- Legyen f:[a,b]  R integrálható. Ha f folytonos az u ∈ [a,b] pontban, akkor ∫ f differenciálható u-ban és
R integrálható. Ha f folytonos az u ∈ [a,b] pontban, akkor ∫ f differenciálható u-ban és
Bizonyítás. f folytonos u-ban, ezért tetszőleges ε > 0-ra létezik olyan δ > 0, hogy f|B(δ,u) ⊆ Bε(f(u)), azaz:
Írjuk fel a deriváltra a különbségi hányadost! Legyen x,y olyan, hogy az u δ sugarú környezetébe esik. Ekkor az integrál intervallum szerinti additivitása miatt:
Ha most a tirviális alsó és felső becslést vesszük:
s mivel ε tetszőleges volt, ezért f(u) nem más, mint az integrálfüggvény u-beli különbségi háényadosának határértéke (az x=u helyettesítéssel). QED
Látható, hogy a bizonyításban többet láttunk be. Egyfajta u körüli "egyenletes differenciálatóságot", az úgy nevezett erős differenciálhatóságot. Ez azért lehet fontos, mert ha az integrálfüggény deriváltja nem nulla, akkor nem csak ő, de az inverze is Lipschitz-folytonos, amiből pedig az következik, hogy mind az i.f. mind az inverze nullmértékű halmazt nullmértékűbe képez.
Az integrálfüggvény Lipschitz-tulajdonsága
És persze az integrálfüggvény "nagyon" folytonos, egészen pontosan Lipschitz-tuljadonságú vagy más névven Lipschitz-folytonos, azaz
- létezik olyan L nemnegatív szám, hogy minden x,y ∈ [a,b]-re
azaz létezik olyan L, hogy minden x,y ∈ [a,b]-re
Ugyanis a triviális felső becslésből:
ahol L-nek alkalmas a sup |f| szám.
A Lipschitz-tulajdonság és folytonosság kapcsolatáról lásd még [itt].
Példák
Vizsgáljuk meg növekedés szempontjából az
szinusz integrálisz függvényt!
Primitívfüggvények
Definíció. Azt mondjuk, hogy az f:[a,b]  R függvénynek primitív függvénye az F:[a,b]
R függvénynek primitív függvénye az F:[a,b] R differenciálható függvény, ha F' = f.
R differenciálható függvény, ha F' = f.
Világos, hogy ha F primitív függvénye f-nek, akkor akármilyen konstans C-vel F + C is primitív függvénye f-nek, hisz (F + C)'= F' = f. Ennél több is igaz. Ha f-nek primitívfüggvénye F, akkor f összes primitívfüggvénye F + C alakú, ahol C tetszőleges valós szám. Ez az alábbi fontos tétel közvetlen következménye:
Tétel. Ha az F:[a,b] R differenciálható függvény olyan, hogy F' ≡ 0, akkor létezik olyan C valós szám, hogy F ≡ C.
R differenciálható függvény olyan, hogy F' ≡ 0, akkor létezik olyan C valós szám, hogy F ≡ C.
Bizonyítás. Egyszerűen a Lagrange-tételt kell alkalmazni F egy tetszőleges [a,x]-re történő leszűkítésétre:
azaz
QED
Ha tehát egyáltalán van f-nek van primitív függvénye és F ilyen, akkor ezek halmaza:
Talán fellengzősség, de a fenti tételt néha az integrálszámítás alaptételének nevezik. Ennek egy kiterjesztett formája azonban tényleg méltó erre a névre:
Tétel. Ha az F:[a,b] R differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és F Lipschitz-tulajdonságú, akkor F konstans.
R differenciálható függvény majdnem mindnehol differenciálható, ezekben a pontokban a derivált nulla és F Lipschitz-tulajdonságú, akkor F konstans.
Az alábbi tétel szerint, amit szintén joggal neveznek a kalkulus fundamentális tételének, ha egy integrálható függvénynek van primitív függénye, akkor az integrálfüggvények és primitívfüggvények halmaza egybeesik, sőt:
Tétel. Newton--Leibniz-formula Legyen f:[a,b] R integrálható és létezzen primitív függvénye. Ekkor f mindnen F primitív függvényére:
R integrálható és létezzen primitív függvénye. Ekkor f mindnen F primitív függvényére:
Ez a kalkulus második fundamentális tétele. Érdemes alaposan megvizsgálni a feltételeit, mert tanulságos példákra lelhetünk.
++++++++++++++++++++++++++++++++++++++++++
+ létezik primitív függvénye + Dir
+ +
+ +
+ *********************************************************
+ g' * h' + R-integrálható *
+ * + *
+ * ############### + *
+ * # folytonos # + *
+ * # # + *
+ * ############### + Ent|[0,2] *
+ * + *
+ * + *
+++++++++++++++++*++++++++++++++++++++++++ *
* *
* *
* *
*********************************************************
A Dir Dirichlet-függvények nem létezik primitívfüggvénye, mert ha lenne olyan függvény, aminek ő a deriváltja lenne, akkor ő, mint deriváltfüggvény nem lenne Darboux-tulajdpnságú: két függvényértéke között nem mindent venne fel. Azt is megéztük, hogy R-integrálja sincs. (Bár Lebesgue-integrálja 0.)
Az Ent egészrész függvény integrálható (egy korlátos és zárt intevallumon), mert monoton, de nincs primitív függvénye, mert derivált nem ugorhat.
Legyen g : [-1,1]  R a következő:
R a következő:
Ekkor g differenciálható, így g'-nek g primitívfüggvénye, de tudjuk, hogy g'-nek nem korlátos másodfajú szakadésa van a 0-ban, így g' nem lehet integrálható.
Végül nézzünk példát olyan függvényre, mely nem folytonos, de értelmes rá a N--L-formula. Legyen h: [-1,1]  R a következő:
R a következő:
Ekkor g differenciálható, így g'-nek g primitívfüggvénye, és tudjuk, hogy g' korlátos és csak a 0-ban van egyetlen szakadása, így g' integrálható.
Megjegyezük, hogy a görbe alatti területet nem véges összegekkel, hanem végtelen sorral közelítő Lebesgue-integrál olyan általános, hogy ilyen vagy még általánosabban definiált értelmeben nem integrálható függvényt keresni már komoly matematikai/halmazelméleti kihívást jelent.
A Newton--Leibniz-formula bizonyítása. Belátjuk, hogy a baloldal és a jobboldal abszolút eltérése minden pozitív számnál kisebb. Legyen ε > 0. Ekkor az integrálhatóság miatt létezik olyan δ > 0 szám, hogy minden η ∈ RFδ[a,b] Riamann-felosztásra
A bizonyítás trükkje az, hogy az F(b)-F(a) különbséget a közelító összegben lévő sok taggal, mint teleszkópikus összeggel tudjuk előállítani. Ugyanis a Lagrange-féle középértéktétel miatt egy tetszőlegesen rögzített η ∈ RFδ[a,b] felosztás minden részintervallumán létezik olyan ξi ∈ [xi-1,xi], hogy
Emiatt, ha azt az ξ felosztást választjuk, melynek osztópontjai az &eta osztópontjaival esenek egybe, de a részintervallumokból rendre a ξxi értékeket választja ki, akkor fennáll:
Itt az összeg tagjai úgy esnek össze, ahogy azt a teleszkópikus összegeknél láthatjuk. Végül
s mivel ε tetszőleges volt, ezért az egyenlőség fennáll. QED
Az ábrán van egy különlegesen fontos eset. Amikor az integrandus folytonos, akkor a fügvénynek biztosan létezik primitívfüggvénye. Ez annak a tételnek a duálisa, hogy folytonos függvény integrálható.
Tétel. f ∈ C[a,b], akkor f-nek (biztosan) létezik primitívfüggvénye.
Ugyanis ekkor az integrálfüggvény minden pontban differenciálható, azaz az integrálfüggény primitívfüggvénye f-nek.
Jelölés. Ha f folytonos, akkor indokolt a primitív függvények összességét a
alakban írni, ahol C tetszőleges szám.
Megjegyzés. Ha tehát az a kérdés, hogy melyek a primitív függvényei f-nek, akkor a válasz a fenti kifejezés, ahol a határozatlan integrált szimbolizáló tag általában egy konkrét függvény.
Primitívfüggvény-keresés
Primitívfüggvény-keresésnek két metódusa van. Az egyik a helyettesítéses integrálás, a másik a parciális integrálás. Ezek előtt azonban egy triviális módszer, a deriválási táblázat megfodítása és az integrál eltolásinvarianciájának felhasználása. (Esetleg a lineáris argumentumú alapintegrál kiszámítása.)
Alapintegrálra visszavezethető integrálok
Ha tehát vesszük az elemi függvények és inverzeinek deriválási táblázatát, akkor jobbról balra olvasva megkapjuk az alapintegrálok táblázatát.
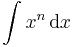
| 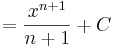
| 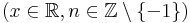
|
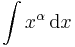
| 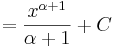
| 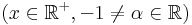
|
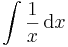
| 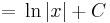
| 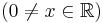
|
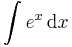
| 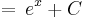
| 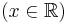
|
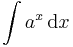
| 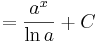
| 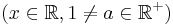
|
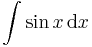
| 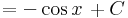
| 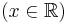
|
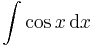
| 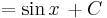
| 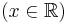
|
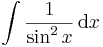
| 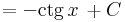
| 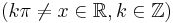
|
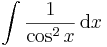
| 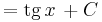
| 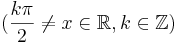
|
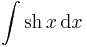
| 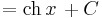
| 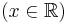
|
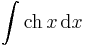
| 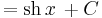
| 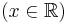
|
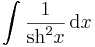
| 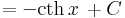
| 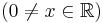
|
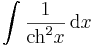
| 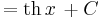
| 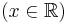
|
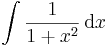
| 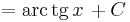
| 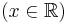
|
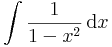
| 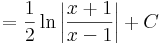
| 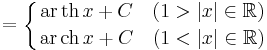
|
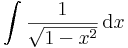
| 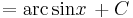
| 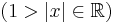
|
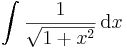
| 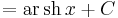
| 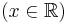
|
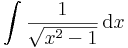
| 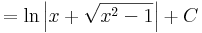
| 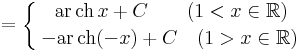
|
Alapintegrálok kiszámítása táblázatból
vagy a legkönnyebben elronthatók:
Alapintegrálok és eltolásinvariancia
Az integrál eltolásinvarianciáját használva:
Lineáris agrumentumú integrandus
A lineáris agrumentumúkra vonatkozó képlet:
ahol F'=f. Hiszen az összetett függvény deriválási szabálya szerint:
Ezzel pl:
Megjegyzés. Érdemes fejünkbe vésni a sin függvény deriváltajainak függvénysorozatát:
- sin
- cos
- − sin
- − cos
- sin
- cos

felfejé haladva integrálunk, lefelé haladva deriválunk.
pl.
Polinom/lineáris alak
itt már érdemes polinomosztással eljárni:
(x^2 + 2) : (x - 1) = x + 1
- x^2 - x
---------
x + 2
- x - 1
--------
3
Néha x2 + 1 nevezőjűre is működik:
Linearizáló formulák
Ezek arra alkalmasak, hogy a sin2, cos2, sh2. ch2 függvényeket (illetve alkalmasan megváltoztatott argumentumú változatukat) ki lehessen integrálni:
Mindezek a következők miatt állnak fenn:
ezért ezeket kivonva ill. összeadva, majd 2-vel elosztva a felső kettőt kapjuk. A másik kettő:
Itt érdemes megjegyezni az Osborne-szabályt: ha egy trigonometrikus azonosságban kicseréljük a megfelelő hiperbolikus függvényekre az összetevőket és minden olyan tag előjelét megváltoztatjuk, melyek két sh szorzatából állnak (speciálisan a sh2-ek elé egy - jelet teszünk), akkor megkapjuk a hiperbolikus azonosságot. Lásd: Osborne-szabály.
Ezek főleg határozott integráloknál adnak "szép" eredményt
Példa.
Helyettesítéses integrálás
Az első keresési eljárás az összetett függvény deriválási szabályának megfordításán alapul.
Tétel. Legyen g:I  J, F: J
J, F: J  R folytonosan differenciálható függvények és f: J
R folytonosan differenciálható függvények és f: J  R pedig olyan, hogy az F' = f, akkor az x
R pedig olyan, hogy az F' = f, akkor az x  f(g(x))
f(g(x))  g'(x)-nek is létezik primitív függvénye és
g'(x)-nek is létezik primitív függvénye és
Bizonyítás. A primitív függvény létezését az garantálja, hogy az integrandus folytonos.
Elegendő ellenőrizni, hogy x  F(g(x)) primitív függvénye x
F(g(x)) primitív függvénye x  f(g(x))
f(g(x))  g'(x)-nek, azaz az előbbi deriváltja az utóbbi:
g'(x)-nek, azaz az előbbi deriváltja az utóbbi:
QED.
...-alakú integrálok
Ebből a tételből származtathatjuk a "... alakú integrálokat":
Példák.
1.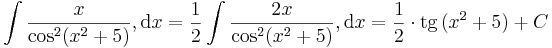 hiszen a "külső" függvény:
hiszen a "külső" függvény:
a "belső" függvény:
2.
hiszen a "külső" függvény:
a "belső" függvény:
3.
hiszen a "külső" függvény:
a "belső" függvény:
4.
hiszen a "külső" függvény:
a "belső" függvény:
Integrálás a helyettesítés elvégzésével
Megjegyzés. Intermezzóként megemlítjük, hogy a helyettesítés elnevezés abból fakad, hogy ekkor lényegében új ismeretlent vezetünk be. Persze az ezzel való számolás egy egészen más szemléletet igényel. A fő képlet ekkor:
ahol el kell végezni az
szimbolikus helyettesítést.
5. (exponenciális helyettesítés)
5. (gyökös helyettesítés)
6. (trigonometrikus helyettesítés)
Parciális integrálás
A helyettesításes integrálás a függvénykompozíció deriválására szolgáló képlet felhasználása volt primitívfüggvény keresésre. Most a szorzási szabályt fogjuk használni.
Tétel. Legyen f,g:[a,b]  R folytonos és F,G:[a,b]
R folytonos és F,G:[a,b]  R differenciálható olyan, hogy F' = f, G' = g. Ekkor az alábbi képletben szereplő összes integrandusnak létezik primitív függvénye és
R differenciálható olyan, hogy F' = f, G' = g. Ekkor az alábbi képletben szereplő összes integrandusnak létezik primitív függvénye és
Bizonyítás. Elég a bizonyítani, hogy a jobb oldal deriváltja a baloldali integrandus. Ehelyett egy kicsit másként csináljuk: belátjuk, hogy az FG függvény primitívfüggvénye az fG + Fg függvénynek, majd kefejezzük velőle a fenti formula baloldalát:
tehát
amiből már következik a fenti formula. QED.
Polinom szor exp, trig, hip
Az első alkalmazás az, amikor a egymás után parciális integrálásokkal polinommentes formulává alakítjuk az integrandust. Ekkor a fenti képlet F-je a polinom, amiből egyel alacsonyabb fokú polinomszoros integrandus keletkezik az ∫fG integrál esetén.
Hiszen
Egy hasonló:
Hiszen
Rekurziós integrálok, formulák
1.
az
szereposztással. A formulában visszatért a keresett integrál, így ezt kifejezve:
2.
amiből
tehát kétszeri parciális integrálással értük el.
3. Rekurziós formulát kapunk az alábbi In alakú integrálokra:
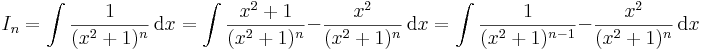 az utolsó tagot parciálisan integráljuk ki:
az utolsó tagot parciálisan integráljuk ki:
azaz In kifejezhető In − 1-segítségével.
Inverzfüggvények integrálja
Az
trükk sokszor alkalmas arra, hogy az inverz függvények integrálját parciálisan kiintegráljuk, hiszen az inverz függvények deriváltjának képlete az utolsó tényezőt a kezünkre játssza. Speciálisan a módszer alkalmas az összes ln, arc és ar függvény kiintegrálására.
1.
![\eta:\{[x_0,x_1],[x_2,x_3], ..., [x_{n-1},x_n] \}\to [a,b]\,](/upload/math/4/7/6/476cb30799b8150e22a3bbef00e5cfff.png)
![\sigma_f(\eta)=\sum\limits_{i=1}^nf(\eta([x_{i-1},x_i])\cdot|x_i-x_{i-1}|)](/upload/math/a/4/d/a4db058bcff2cbe8bb2d424ae853e44c.png)
![(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}[a,b])(|\sigma_f(\eta)-I|< \varepsilon)](/upload/math/a/d/e/adefce08419bf5508ef3b14d65782293.png)
![\int f:[a,b]\to \mathbf{R}, x\mapsto\int\limits_{a}^xf\,](/upload/math/3/2/1/32197d847adb794644364ba069a88472.png)
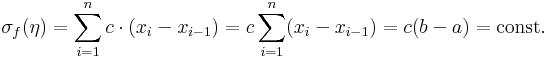
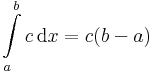
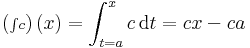
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{x}, & \mathrm{ha} & x\in (0,1] \\\\ 1854, & \mathrm{ha} & x=0 \end{matrix}\right.](/upload/math/f/e/2/fe28b4484356f462699457435a0cb0ad.png)
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in \mathbf{Q} \\\\ 0, & \mathrm{ha} & x\in \mathbf{R}\setminus\mathbf{Q} \end{matrix}\right.](/upload/math/a/c/3/ac329e8012056e15927ee566fbe98db2.png)
![f\in \mathrm{R}[a,b]\;\Leftrightarrow\;(f\in \mathrm{B}[a,b]\;\wedge\; \mathrm{m}(\mathrm{discon}(f))=0)](/upload/math/d/2/c/d2c21ed005e06a1ea4ae356da5bcd67c.png)
![f:[-1,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}|x|\sin(\frac{1}{x}), & \mathrm{ha} & x\ne 0 \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.](/upload/math/6/a/b/6ab08e2bf7e7ec46f393164c1e44b064.png)
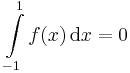
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{2^{i+1}}, & \mathrm{ha} & \frac{1}{2^{i+1}}<x\leq\frac{1}{2^i} \\\\ 0, & \mathrm{ha} & x= 0\end{matrix}\right.](/upload/math/a/5/c/a5cad5a3691bdc5262070039cb1e2b8a.png)
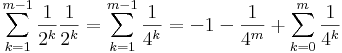
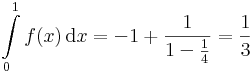
![f:[0,1]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}\frac{1}{1+\sin(\frac{1}{x})}, & \mathrm{ha} & x\ne \frac{1}{-\frac{\pi}{2}+2k\pi},0\\\\ 0, & \mathrm{ha} & x= \frac{1}{\frac{-\pi}{2}+2k\pi},0\end{matrix}\right.](/upload/math/6/6/4/664caab5c66ee826755e5fbadea1a63f.png)

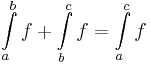
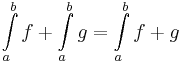
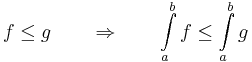
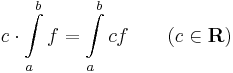
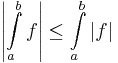
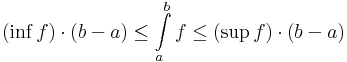
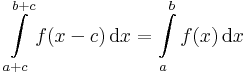
![f:[0,2]\to \mathbf{R},\;x\mapsto\left\{\begin{matrix}1, & \mathrm{ha} & x\in [0,1) \\\\ 2, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.](/upload/math/7/f/a/7fad0719708fc616be5c846dcd569210.png)
![T(x)=\left\{\begin{matrix}x\cdot 1, & \mathrm{ha} & x\in [0,1) \\\\ 1+2(x-1), & \mathrm{ha} & x\in [1,2] \end{matrix}\right\}=\left\{\begin{matrix}x, & \mathrm{ha} & x\in [0,1) \\\\ 2x-1, & \mathrm{ha} & x\in [1,2] \end{matrix}\right.](/upload/math/9/5/4/9549a45ddcebb273339d1fd2d656ae7f.png)
![T'=f|_{[0,1)\cup(1,2]}](/upload/math/5/5/8/5581144dddd6d5c01260374f851b3ad2.png)
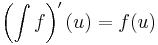
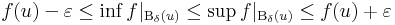
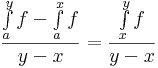
![f(u)- \varepsilon\leq\inf f|_{[x,y]}=\frac{\inf f|_{[x,y]}\cdot (y-x)}{y-x}\leq\frac{\int\limits_{x}^yf}{y-x}\leq \frac{\sup f|_{[x,y]}\cdot (y-x)}{y-x}\sup f|_{[x,y]}\leq f(u)+ \varepsilon](/upload/math/c/b/c/cbc5a59eb88d4357370874d682a9d864.png)
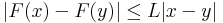
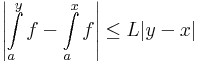
![\left|\int\limits_{a}^y f-\int\limits_{a}^x f\right|\leq \left|\int\limits_{x}^y f\right|\leq \int\limits_{x}^y|f|\leq \sup |f|\,|_{[x,y]}\cdot |y-x|\leq\sup |f|\cdot |y-x|](/upload/math/3/3/b/33be882988814546252b83732f4bbe64.png)
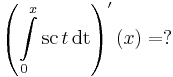
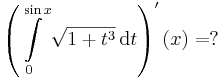
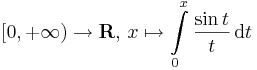
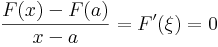
![F(a)=F(x)\,\quad\quad (x\in [a,b])](/upload/math/8/8/5/8854a00d6bd4ec6a3b6b485cea6de8be.png)
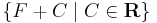
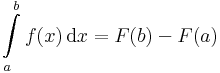
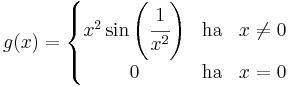
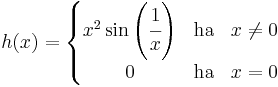
![\left|\sum\limits_{i=1}^nf(\eta([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})-\int\limits_a^b f\right|< \varepsilon](/upload/math/9/d/3/9d3672f524d1f0e21ec0854ac80d8050.png)
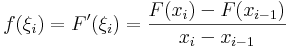
![\sum\limits_{i=1}^nf(\xi([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})=\sum\limits_{i=1}^n\frac{F(x_i)-F(x_{i-1})}{x_i-x_{i-1}}\cdot (x_i-x_{i-1})=\sum\limits_{i=1}^n F(x_i)-F(x_{i-1})=F(b)-F(a)\,](/upload/math/1/a/8/1a8ec296fefab6f2f32b5b9ee9e0c93b.png)
![\left|\sum\limits_{i=1}^nf(\eta([x_i,x_{i-1}]))\cdot (x_i-x_{i-1})-\int\limits_a^b f\right|=\left|F(b)-F(a)-\int\limits_a^b f\right|< \varepsilon](/upload/math/5/9/a/59a5c1421b3b99f2c12e7a7c576d5323.png)
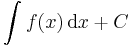
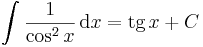
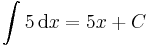
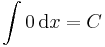
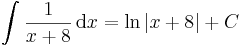
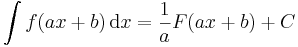
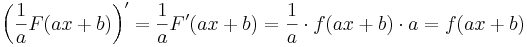
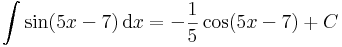
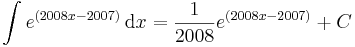
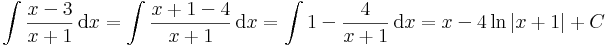
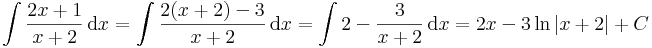
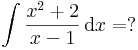
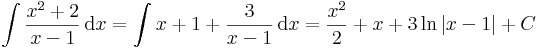
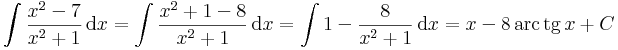
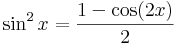
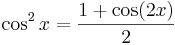
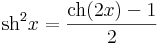
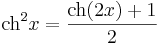
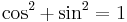
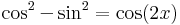
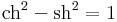
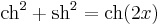
![\int\limits_{0}^{\pi}\sin^2 x\mathrm{d}x=\int\limits_{0}^{\pi}\frac{1-\cos(2x)}{2}\mathrm{d}x=\left[\frac{1}{2}x-\frac{1}{4}\sin(2x)\right]_0^\pi=\frac{\pi}{2}](/upload/math/b/b/1/bb1ac1a5fc003d49e4d0b180372d7001.png)
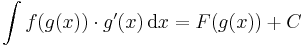
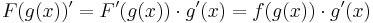
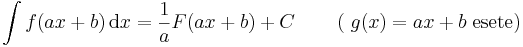
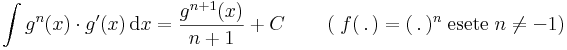
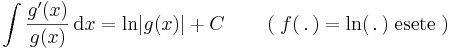
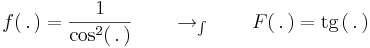
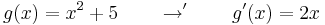
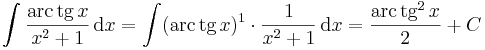
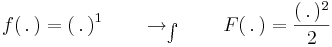
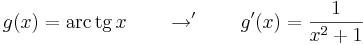
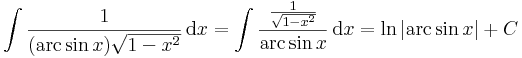
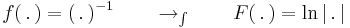
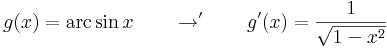
![\int x^2\sqrt[2008]{\mathrm{sh}\,x^3}\cdot \mathrm{ch}\,(x^3)\,\mathrm{d}x= \frac{1}{3}\int \sqrt[2008]{\mathrm{sh}\,x^3}\cdot (3x^2\mathrm{ch}\,(x^3))\,\mathrm{d}x=\frac{2008}{3\cdot 2009}(\mathrm{sh}\,x^3)^{\frac{2009}{2008}}+C](/upload/math/1/b/3/1b3c959834da02ddb24710fafb3e3b3e.png)