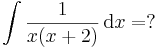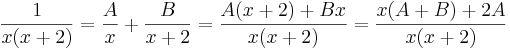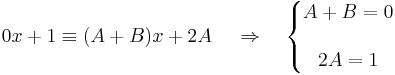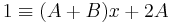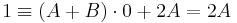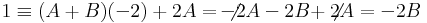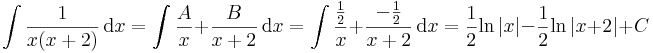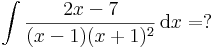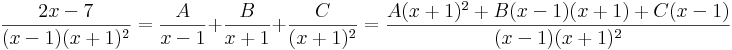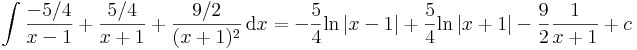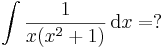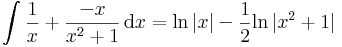Matematika A1a 2008/12. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) ({) |
Mozo (vitalap | szerkesztései) (→A nevező egyszeres gyökökkel rendelkező elsőfokúak szorzata) |
||
| 22. sor: | 22. sor: | ||
Végül visszahelyettesítve a felbontott alakba: | Végül visszahelyettesítve a felbontott alakba: | ||
:<math>\int\frac{1}{x(x+2)}\,\mathrm{d}x=\int\frac{A}{x}+\frac{B}{x+2}\,\mathrm{d}x=\int\frac{\frac{1}{2}}{x}+\frac{-\frac{1}{2}}{x+2}\,\mathrm{d}x=\frac{1}{2}\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x+2|+C</math> | :<math>\int\frac{1}{x(x+2)}\,\mathrm{d}x=\int\frac{A}{x}+\frac{B}{x+2}\,\mathrm{d}x=\int\frac{\frac{1}{2}}{x}+\frac{-\frac{1}{2}}{x+2}\,\mathrm{d}x=\frac{1}{2}\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x+2|+C</math> | ||
| + | |||
| + | ===A nevező többszörös gyökökkel rendelkező elsőfokúak szorzata=== | ||
| + | :<math>\int\frac{2x-7}{(x-1)(x+1)^2}\,\mathrm{d}x=?</math> | ||
| + | ::<math>\frac{2x-7}{(x-1)(x+1)^2}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x+1)^2}=\frac{A(x+1)^2+B(x-1)(x+1)+C(x-1)}{(x-1)(x+1)^2}</math> | ||
| + | Ekkor a gyökmódszerrel: | ||
| + | x=-1-re: -2C=2(-1)-7=-9, azaz C=9/2. | ||
| + | x=1-re 4A=-5, A=-5/4 | ||
| + | és egy szabadon válaztott egyszerű: x=0-ra: A-B-C=-7, ahonnan B=A-C+7, azaz B=-5/4-18/4+28/4= 5/4 | ||
| + | |||
| + | Az integrál: | ||
| + | :<math>\int\frac{-5/4}{x-1}+\frac{5/4}{x+1}+\frac{9/2}{(x+1)^2}\,\mathrm{d}x=-\frac{5}{4}\mathrm{ln}\,|x-1|+\frac{5}{4}\mathrm{ln}\,|x+1|-\frac{9}{2}\frac{1}{x+1}+c</math> | ||
| + | |||
| + | ===A nevező egyszeres multiplicitású irreducibilis tényezők szorzata=== | ||
| + | :<math>\int\frac{1}{x(x^2+1)}\,\mathrm{d}x=?</math> | ||
| + | Itt a keresendő alak: | ||
| + | <math>\frac{1}{x(x^2+1)}=\frac{A}{x}+\frac{Bx+C}{x^2+1}=\frac{A(x^2+1)+Bx^2+Cx}{x(x^2+1)}</math> | ||
| + | vegyes módszerrel: | ||
| + | x=0: A=1 | ||
| + | C=0, mert nincs a bal oldalon elsőfokú | ||
| + | B=-A, mert másodfokú sincs. | ||
| + | :<math>\int\frac{1}{x}+\frac{-x}{x^2+1}\,\mathrm{d}x=\mathrm{ln}\,|x|-\frac{1}{2}\mathrm{ln}\,|x^2+1|</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
[[Kategória:Matematika A1]] | [[Kategória:Matematika A1]] | ||
A lap 2008. december 10., 11:28-kori változata
Tartalomjegyzék |
Integrálás parciális törtekre bontással
A nevező egyszeres gyökökkel rendelkező elsőfokúak szorzata
Két polinom azonos, akkor és csak akkor, ha a megfelelő együtthatók rendre egyenlők:
ahonnan: A=1/2, B=-1/.
Az egyenletrendszer megoldásán kívül van egy másik módszer is:
-ben először tegyük x-be az egyik gyököt, az 0-t:
innen A=1/2, majd a másik gyököt:
azaz B=-1/2.
Végül visszahelyettesítve a felbontott alakba:
A nevező többszörös gyökökkel rendelkező elsőfokúak szorzata
Ekkor a gyökmódszerrel: x=-1-re: -2C=2(-1)-7=-9, azaz C=9/2. x=1-re 4A=-5, A=-5/4 és egy szabadon válaztott egyszerű: x=0-ra: A-B-C=-7, ahonnan B=A-C+7, azaz B=-5/4-18/4+28/4= 5/4
Az integrál:
A nevező egyszeres multiplicitású irreducibilis tényezők szorzata
Itt a keresendő alak:
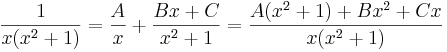 vegyes módszerrel:
x=0: A=1
C=0, mert nincs a bal oldalon elsőfokú
B=-A, mert másodfokú sincs.
vegyes módszerrel:
x=0: A=1
C=0, mert nincs a bal oldalon elsőfokú
B=-A, mert másodfokú sincs.