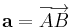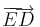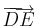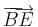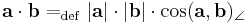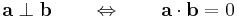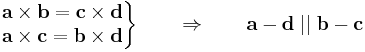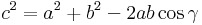Matematika A1a 2008/2. gyakorlat
Mozo (vitalap | szerkesztései) (→Koordináta reprezentációk) |
Mozo (vitalap | szerkesztései) (→Összeadás, számmal való szorzás) |
||
| (egy szerkesztő 8 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | [[Matematika A1a 2008|<Matematika A1a 2008]] | + | <sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub> |
| − | + | A vektoralgebra felépítésére vonatkozóan lásd: ([http://members.chello.hu/molnar.zoltan13/Main/vektoralgebra.pdf pdf]) | |
| − | A vektoralgebra felépítésére vonatkozóan lásd: ([http:// | + | |
==Vektorok== | ==Vektorok== | ||
| − | Irányított egyenes szakaszok között definiálunk egy "azonosság" relációt, lényegben | + | Irányított egyenes szakaszok között definiálunk egy "azonosság" relációt, lényegben azzal, hogy az egyenlő nagyságú, egymással párhuzamos, azonos irányú egyenes szakaszokat azonosnak vesszük. Egymással azonosok egy halmazát nevezzük vektornak, elemeit a vektor egy reprezentánsának. Jelben: ha '''a''' vektor, akkor |
:<math>\mathbf{a}=\overrightarrow{AB}</math> | :<math>\mathbf{a}=\overrightarrow{AB}</math> | ||
jelöli, hogy <math>\overrightarrow{AB}\in \mathbf{a}</math>. | jelöli, hogy <math>\overrightarrow{AB}\in \mathbf{a}</math>. | ||
| 37. sor: | 36. sor: | ||
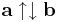
Az '''a''' ''ellentett vektora'' az a -'''a''' vektor, melyre |-'''a'''| = |'''a'''|, <math>\mathbf{a}\uparrow\downarrow(-\mathbf{a})</math>. | Az '''a''' ''ellentett vektora'' az a -'''a''' vektor, melyre |-'''a'''| = |'''a'''|, <math>\mathbf{a}\uparrow\downarrow(-\mathbf{a})</math>. | ||
| − | ( | + | (Olyan tulajdonságú, mint a valós számok összeadása: kommutatív, asszociatív, '''0''' -t bármihez adva, amaz nem változik, ellentettjét a vektorhoz adva '''0'''-t kapunk.) |
'''Számmal való szorzás.''' Legyen '''a''' vektor, λ valós szám. Ekkor | '''Számmal való szorzás.''' Legyen '''a''' vektor, λ valós szám. Ekkor | ||
| 84. sor: | 83. sor: | ||
'''3. Feladat.''' Legyen ABC háromszög, S a súlypontja, F az AB felezéspontja. Határozzuk meg, hogy az ABC háromszög területének hanyadrésze az AFS háromszog területe. | '''3. Feladat.''' Legyen ABC háromszög, S a súlypontja, F az AB felezéspontja. Határozzuk meg, hogy az ABC háromszög területének hanyadrésze az AFS háromszog területe. | ||
| + | |||
| + | vagy | ||
| + | |||
| + | Igazoljuk, hogy az egyenlőszárú háromszög magassága felezi az alapot! | ||
'''4. Feladat.''' Igazoljuk, hogy | '''4. Feladat.''' Igazoljuk, hogy | ||
| 90. sor: | 93. sor: | ||
\mathbf{a}\times\mathbf{c}=\mathbf{b}\times\mathbf{d} | \mathbf{a}\times\mathbf{c}=\mathbf{b}\times\mathbf{d} | ||
\end{matrix}\right\}\quad\quad | \end{matrix}\right\}\quad\quad | ||
| − | \Rightarrow\quad\quad \mathbf{a}-\mathbf{ | + | \Rightarrow\quad\quad \mathbf{a}-\mathbf{d}\;||\;\mathbf{b}-\mathbf{c}</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Házi feladatok== | ==Házi feladatok== | ||
A lap jelenlegi, 2014. február 17., 22:14-kori változata
A vektoralgebra felépítésére vonatkozóan lásd: (pdf)
Tartalomjegyzék |
Vektorok
Irányított egyenes szakaszok között definiálunk egy "azonosság" relációt, lényegben azzal, hogy az egyenlő nagyságú, egymással párhuzamos, azonos irányú egyenes szakaszokat azonosnak vesszük. Egymással azonosok egy halmazát nevezzük vektornak, elemeit a vektor egy reprezentánsának. Jelben: ha a vektor, akkor
jelöli, hogy 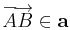 .
.
Az a vektor hossza
- |a|
nem más, mint mely bármely reprezentánsának hossza.
Nullvektor az aminek a hossza 0.
Két vektor párhuzamos:
- a || b
ha van egy-egy reprezentánsuk, melyek egyenese párhuzamos. 0 || a minden a vektorra definíció szerint.
Két párhuzamos vektor azonos állású vagy irányítású
ha a reprezentánsaik azonos irányításúak; a 0 mindennek azonos irányú. Ellenkező esetben:
Tétel. a = b, akkor és csak akkor, ha
- |a| = |b| és
- a || b és
-
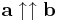
Vektorműveletek
Összeadás, számmal való szorzás
Összeadás. Legyen a és b két vektor és 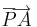 ,
, 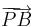 rendre a két vektor azonos kezdőpontból felmért reprezentánsa, legyen továbbá PACB paralelogramma (P-vel szemközt: C). Ekkor a + b vektor definíció szerint az a c vektor, melyet
rendre a két vektor azonos kezdőpontból felmért reprezentánsa, legyen továbbá PACB paralelogramma (P-vel szemközt: C). Ekkor a + b vektor definíció szerint az a c vektor, melyet 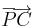 reprezentál.
reprezentál.
Kivonás: a - b =def a + (-b)
Az a ellentett vektora az a -a vektor, melyre |-a| = |a|, 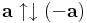 .
.
(Olyan tulajdonságú, mint a valós számok összeadása: kommutatív, asszociatív, 0 -t bármihez adva, amaz nem változik, ellentettjét a vektorhoz adva 0-t kapunk.)
Számmal való szorzás. Legyen a vektor, λ valós szám. Ekkor
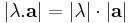 ,
,
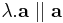 ,
,
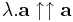 , ha λ > 0 és
, ha λ > 0 és 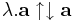 , ha λ < 0
, ha λ < 0
(Széttagolja a valós és a vektorösszeget, felcserélhető a valós szorzással, az 1-gyel való szorzás azonos az identitással.)
1. Feladat. ABCDEF egy szabályos hatszög. Fejezzük ki az a = 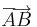 és b =
és b = 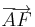 vektorok összegével/számszorosával a
vektorok összegével/számszorosával a
vektorokat!
Skaláris szorzás
Az a és b vektorok skaláris szorzata az
szám.
(Széttagolja az összeget, felcserélhető a számmal való szorzással (mindkét változójában)).
e egységvektor, ha |e| = 1.
Geometriai tulajdonsága.
- Ha e egységvektor, akkor v
 e a v-nek az e egyenesére eső merőleges vetületének előjeles hossza.
e a v-nek az e egyenesére eső merőleges vetületének előjeles hossza.
- a, b nem nullvektorok, akkor
-
2. Feladat. Legyen ABCD egy téglalap, melynek AB oldala 5 egység, AD oldala 4 egység. Legyen a az 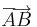 irányú egységvektor, és b az
irányú egységvektor, és b az 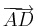 irányú egységvektor. Legyen továbbá E az AD felezéspontja, G az AB B-hez közelebbi ötödölőpontja és az egyel beljebbi az F. Igazolja, hogy GE merőleges FC-re!
irányú egységvektor. Legyen továbbá E az AD felezéspontja, G az AB B-hez közelebbi ötödölőpontja és az egyel beljebbi az F. Igazolja, hogy GE merőleges FC-re!
Vektoriális szorzás
Az a és b térvektorok vektoriális szorzata az a c = a × b vektor, melyre
-
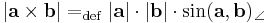
- merőleges az a és b által kifeszített síkra,
- irányítása olyan, hogy (a, b, a × b) ilyen sorrendben jobbrendszert alkot, azaz a jobb kéz hüvelyk, mutató és középső ujját kifeszíthetjük "fájdalommentesen" úgy, hogy rendre a a, b, a × b vektorok irányát kapjuk.
Széttagolja az összeget, felcserélhető a számmal való szorzással, de nem asszociatív és nem kommutatív, bár antikommutatív, azaz a szorzat ellenkezőjébe megy át a két tényező felcserélésével kapott szorzat.
Geometriai tulajdonsága.
- |a × b| az a és b által kifeszített paralelogramma területe.
-
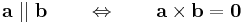
3. Feladat. Legyen ABC háromszög, S a súlypontja, F az AB felezéspontja. Határozzuk meg, hogy az ABC háromszög területének hanyadrésze az AFS háromszog területe.
vagy
Igazoljuk, hogy az egyenlőszárú háromszög magassága felezi az alapot!
4. Feladat. Igazoljuk, hogy
Házi feladatok
- Igazolja, hogy az paralelogramma átlóinak felezőpontjai egybeesnek!
- Igaz-e:
- ha ab = 0, akkor a és b közül legalább az egyik nulla.
- ha ab = ac, és a ≠ 0, akkor b = c
- ha ab = ac, akkor vagy b - c || a, vagy b - c
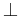 a
a
- Igaz-e:
- ha a×b = 0, akkor a és b közül legalább az egyik nulla.
- ha a×b = a×c, és a ≠ 0, akkor b = c
- ha a + b + c = 0, akkor a×b = b×c = c×a
-
- Igazolja a Thalész-tételt (azaz, hogy ha egy szakasz fölé, mint átmérő fölé kört rajzolunk, akkor a kör bármely (szakaszon kívüli) pontjából a szakasz két végpontja derékszög alatt látszik)!
- Igazolja a koszinusztételt, azaz hogy az a,b,c oldalú háromszögben (γ a c-hez tartozó szög)