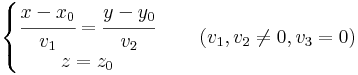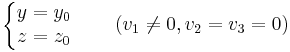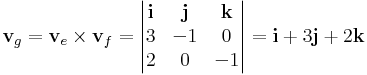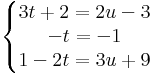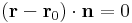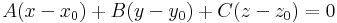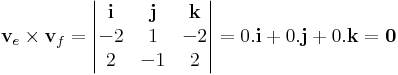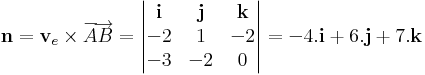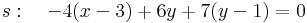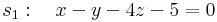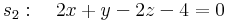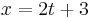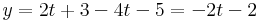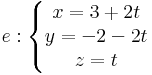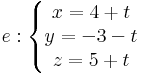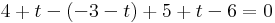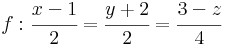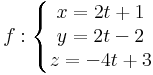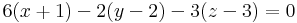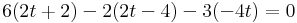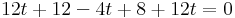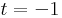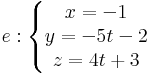Matematika A1a 2008/3. gyakorlat
Tartalomjegyzék |
Koordináta reprezentációk
Lineáris kombinációnak nevezzük a
alakú kifejezéseket, ahol a λ-k számok, az a-k vektorok.
Tétel.
- Ha b1 és b2 két nempárhuzamos vektor a síkban, akkor a sík minden vektora egyértelműen előáll ezek lineáris kombinációjaként:
- Ha b1, b2 és b3 három, nem egy síkban lévő vektor, akkor a tér minden vektora egyértelműen előáll ezek lineáris kombinációjaként:
Síkban két nempárhuzamos vektor halmazát, térben három nem egysíkban lévő vektor halmazát bázisnak nevezünk. Ha ezek egységhosszúságúak és páronként merőlegesen egymásra, akkor ortonormált bázist alkotnak. A jobbsodrású (v.ö.: jobbcsvarszabály) ortonormált bázis a térben az (i, j, k).
Egy v térvektornak B = (b1, b2, b3) bázisra vonatkozó koordinátareprezentációja az az oszlopmátrix, melynek elemei rendre az előző tételbeli egyértelműen létező λ-k:
A vektorműveletek a koordinátareprezentációban a következők lesznek.
Külön fontos a vektoriális szorzat esetén megemlíteni a
"szimbolikus" determinánssal történő kiszámolási módot és a skaláris szorzást, mint mátrixszorzást:
Egyenes
Legyen r0 az e egyenes egy pontjának helyvektora, v az irányvektora. Ekkor az egyenes bármely r pontja előáll (alkalmas t valós paraméterrel)
alakban, hiszen az r - r0 vektor párhuzamos az egyenessel (sőt: az egyesben van), így a v irányvektor skalárszorosa. A t jelölés az "időre" utal. Ha feltételezzük, hogy egy pont sebessége az egyenesen v, akkor t azt jelenti, hogy az r0-végpontából az r végpontjába mennyi idő alatt jutunk el.
A fenti egyenletet az e egyenes paraméteres vektoregyenletének nevezzük. Ha felírjuk koordinátareprezentációban, akkor a
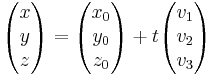 vagyis a
vagyis a 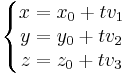
egyenletrendszert kapjuk, melyet az e egyenes paraméteres egyenletrendszerének nevezünk. Persze itt [r0]=(x0,y0, z0), [r]=(x,y, z) és [v]=(v1,v2, v3). <-- Kiküszöbölhetjük t-t, ha minden egyenletetből kivonjuk az adott pont megfelelő komponensét és ezután elosztunk az irányvektor megfelelő komponensével, feltéve, hogy ezek nem nullák:
Ezt nevezzük az egyenes paramétermentes egyenletrendszerének. Ha valamelyik nulla, akkor a következő típusokkal van dolgunk:
illetve
!--> 1. Feladat. Írjuk fel annak az egyenesnek az egyenletrendszerét, mely merőleges mind az e, mind az f egyenesre és áthalad a P0 = (1,2,0) ponton.
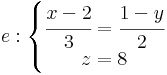 és
és 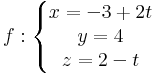
Megoldás. Olvassuk le az irányvektorokat! ve = (3,-1,0) és vf = (2,0,-1). Ezekre merőleges vektort vektoriális szorzattal készítünk:
Azaz:
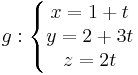
Két egyenes kölcsönös helyzetével kapcsolatban a következő lehetőségek vannak:
- e | | f (ennek kritériuma
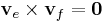 ) ekkor
) ekkor
- vagy egybeesnek (amikoris van közös pontjuk),
- vagy különbözőek (ha nincs)
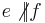 (ennek kritériuma
(ennek kritériuma 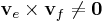 ) ekkor:
) ekkor:
- vagy metszőek (amikoris van közös pontjuk),
- vagy kitérőek (ha nincs)
2. Feladat. Határozzuk meg az
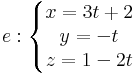 és
és 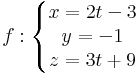
egyenletrendszerekkel megadott egyenesek kölcsönös helyzetét!
Megoldás. Két egyenes pontosan akkor párhuzamos, ha irányvektoraik párhuzamosak. Ezek: (3,-1,-2) és (2,0, 3), azaz biztosan nem párhuzamosak, mert a komponens, amelyik 0, nem áll elő nemnullák szorzataként. Közös pontot az egyenletrendszer megoldásával találhatunk (ha egyáltalán van).
három egyenlet, két ismeretlen, ezért a feladat túlhatározott, azaz általában nincs megoldása. Most tényleg nincs, mert ha t=1, akkor 3u=-10 és 2u=8, ami lehetetlen.
Sík
Legyen r0 az s sík egy pontjának helyvektora, n a normálvektora, azaz egy olyan nemnulla vektor, mely merőleges a síkra (azaz a sík minden pontjára merőleges). Ekkor a sík bármely r pontjára igaz lesz:
hiszen az r - r0 vektor merőleges a sík mormálvektorára, így skaláris szorzatuk 0.
Ha felírjuk koordinátákkal, ahol legyen n = (A,B,C), akkor az
egyenlehez jutunk, melyet az s sík egyenletének nevezünk.
3. Feladat. Írjuk fel annak a síknak az egyenletét, mely áthalad a P = (3,0,1) ponton és párhuzamos az e és f egyenesek által kifeszített síkkal, ha van ilyen.
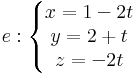 és
és 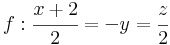
Megoldás. Olvassuk le az irányvektorokat! ve = (-2,1,-2) és vf = (2,-1,2). A sík számára normálvektort úgy kapunk, ha ezekre merőleges vektort készítünk:
ami azonban nem alkalmas normálvektornak. Világos, hogy ez a jelenség amiatt lépett föl, mert a két egyenes párhuzamos egymással. Készítsünk tehát a síkjukban lévő nempárhuzamos vektorokat!
Az e-n egy pont az A = (1,2,0), az f-en: B = (-2,0,0), melyek a t = 0 értékadás által lettek kiválasztva. Legyen u az A-ból B-be menő vektor, mely a (-3,-2,0). Ekkor jó lesz normálvektornak a
A sík így:
4. Feladat. Írjuk fel az alábbi egyenletekkel megadott síkok metszésvonalának egyenletét!
Megoldás. A metszésvonal pontjai kielégítik mindkét egyenletet, így az összegüket is:
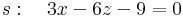 illetve
illetve 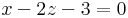
Most gyakorlatilag azt csináltuk, hogy felíruk az n1 + n2 normálvektorú, a metszésvonalon áthaladó sík egyenletét. Ha keresünk ezen egy olyan pontot, mely az s1-en is rajta van, akkor találtunk egy közös pontoto. Kettő ilyen kéne. Válasszuk ki például a z = t síkon egy s-beli pontot, ehhez ugyanis ekkor
tartozik. Ehhez pedig az s1 miatt:
De t helyett bármi állhat, így megkaptuk a metszésvonal összes pontját:
ahol a paraméter a z = t.
5. Feladat. Tükrözzük a P = (4,-3,5) pontot az s: x - y + z - 6 = 0 egyenletű síkra!
Megoldás. A P-ből s-re bocsátott merőleges D döféspontját kell meghatározni, majd kiszámítani a p + 2.(d-p) vektort. Az s-re merőleges e egyenes irányvektora nem más, mint a sík normálvektora:
- n = (1,-1,1)
így a P adott ponttal:
A döféspont ennek a sík egyenletébe helyettesítésével adódik:
innen:
- 6t=-6 és t=-1
Ekkor a döféspont koordinátáit a t=-1 helyettesítéssel nyerjük az egyenletrendszerből: D = (3,-2,4)
- P' = p + 2.(d-p) = (4,-3,5) + 2.(-1,1,-1)=(2,-1,3)
6. Feladat. Határozzuk meg annak az e egyenesnek az egyenletét, mely illeszkedik a P = (-1,2,3) pontra, merőleges az a = (6,-2,-3) vektorra és metszi az
egyenest.
Megoldás. Tudjuk, hogy vektor akkor és csak akkor merőleges egy síkra, ha a sík minden egyenesére merőleges. Ha tehát felírjuk az a normálvektorú, P-n áthaladó s síkot, akkor abban benne lesz e. Hogy merre lesz, azt f árulja el, mert ahol döfi a síkot f, ott lesz e és f metszéspontja. Ez azért van, mert e rajta van s-en, így metszéspontja f-fel szintén s-ben van. Ám, pont ebben a pontban döfi f az s-t.
f paraméteres egyenletrendszere:
s egyenlete:
A döféspont:
Azaz D = (-1,-3,7).
e irányvektora a PD vektor: (0,-5,4)
e paraméteres egyenletrendszere:
Házi feladatok
- Határozza meg annak a síknak az egyenletét, mely tartalmazza az e: x=1-2t, y=2+t, z=-1-t egyenletrendszerű egyenest és a P = (0,1,-2) pontot!
- Határozza meg a 3x+2y-z=3 és x-y+3z=1 egyenletű síkok metszésvonalával párhuzamos, a P = (1,2,3) ponton áthaladó egynenes egyenletét.
További feladatok. A megoldásoknál ajánlott a (pdf) segédlet utolsó oldalát áttanulmányozni.
- Határozzuk meg a 2. és 3. feladatban említett egynespárok távolságát!
- Határozzuk meg a 2. feladatban említett egynespárok szögét!
- Határozzuk meg a 4. feladatban említett síkpárok szögét!
- Határozzuk meg az 5. feladatban említett P és s távolságát!
- Határozzuk meg a 4. feladatban említett síkpárok esetén az "s1 + s2" és a z irányba 5-tel eltolt másának távolságát!
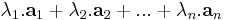
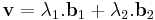
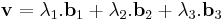
![[\mathbf{v}]_B=\begin{bmatrix}\lambda_1\\ \lambda_2\\ \lambda_3
\end{bmatrix}](/upload/math/1/e/7/1e7cb0a7c3153ae8f3dfd1122069609b.png)
![[\mathbf{a}+\mathbf{b}]=\left[
\begin{matrix}
a_1+b_1\\
a_2+b_2\\
a_3+b_3
\end{matrix}
\right],\quad\quad[\lambda.\mathbf{a}]=\left[
\begin{matrix}
\lambda\cdot a_1\\
\lambda\cdot a_2\\
\lambda\cdot a_3
\end{matrix}
\right],](/upload/math/8/c/1/8c13a007ed640a0e01dd1112186b0430.png)
![\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3,\quad\quad[\mathbf{a}\times\mathbf{b}]=\left[
\begin{matrix}
\;\;a_2b_3-b_2a_3\\
-a_1b_3+b_1a_3\\
\;\; a_1b_2-b_1a_2
\end{matrix}
\right]](/upload/math/4/8/f/48ff379df1c0ffd1a82918295614b029.png)
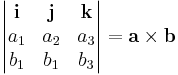
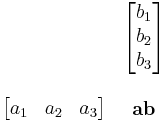
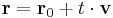
![\frac{x-x_0}{v_1}=\frac{y-y_0}{v_2}=\frac{z-z_0}{v_3}\quad[=t], \quad\quad v_1,v_2,v_3\ne 0](/upload/math/6/3/d/63d398c7d1b5c45bea221988eef68f5b.png)