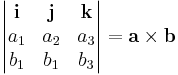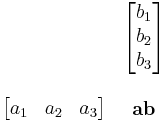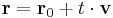Matematika A1a 2008/3. gyakorlat
Koordináta reprezentációk
Lineáris kombinációnak nevezzük a
alakú kifejezéseket, ahol a λ-k számok, az a-k vektorok.
Tétel.
- Ha b1 és b2 két nempárhuzamos vektor a síkban, akkor a sík minden vektora egyértelműen előáll ezek lineáris kombinációjaként:
- Ha b1, b2 és b3 három, nem egy síkban lévő vektor, akkor a tér minden vektora egyértelműen előáll ezek lineáris kombinációjaként:
Síkban két nempárhuzamos vektor halmazát, térben három nem egysíkban lévő vektor halmazát bázisnak nevezünk. Ha ezek egységhosszúságúak és páronként merőlegesen egymásra, akkor ortonormált bázist alkotnak. A jobbsodrású (v.ö.: jobbcsvarszabály) ortonormált bázis a térben az (i, j, k).
Egy v térvektornak B = (b1, b2, b3) bázisra vonatkozó koordinátareprezentációja az az oszlopmátrix, melynek elemei rendre az előző tételbeli egyértelműen létező λ-k:
A vektorműveletek a koordinátareprezentációban a következők lesznek.
Külön fontos a vektoriális szorzat esetén megemlíteni a
determnánssal történő kiszámolási módot és a skaláris szorzást, mint mátrixszorzást:
Egyenes és sík
Legyen r0 az e egyenes egy pontjának helyvektora, v az irányvektora. Ekkor az egyenes bármely r pontja előáll (alkalmas t valós paraméterrel)
alakban, hiszen az r - r0 vektor párhuzamos az egyenessel (sőt: az egyesben van), így a v irányvektor skalárszorosa. A t jelölés az "időre" utal. Ha feltételezzük, hogy egy pont sebessége az egyenesen v, akkor t azt jelenti, hogy az r0-végpontából az r végpontjába mennyi idő alatt jutunk el.
A fenti egyenletet az e egyenes paraméteres vektoregyenletének nevezzük. Ha felÍrjuk koordinátareprezetnációban, akkor a
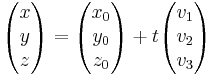 vagyis a
vagyis a 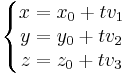
egyenletrendszert kapjuk, melyet az e egyenes paraméteres egyenletrendszerének nevezünk.
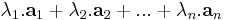
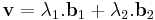
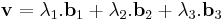
![[\mathbf{v}]_B=\begin{bmatrix}\lambda_1\\ \lambda_2\\ \lambda_3
\end{bmatrix}](/upload/math/1/e/7/1e7cb0a7c3153ae8f3dfd1122069609b.png)
![[\mathbf{a}+\mathbf{b}]=\left[
\begin{matrix}
a_1+b_1\\
a_2+b_2\\
a_3+b_3
\end{matrix}
\right],\quad\quad[\lambda.\mathbf{a}]=\left[
\begin{matrix}
\lambda\cdot a_1\\
\lambda\cdot a_2\\
\lambda\cdot a_3
\end{matrix}
\right],](/upload/math/8/c/1/8c13a007ed640a0e01dd1112186b0430.png)
![\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3,\quad\quad[\mathbf{a}\times\mathbf{b}]=\left[
\begin{matrix}
\;\;a_2b_3-b_2a_3\\
-a_1b_3+b_1a_3\\
\;\; a_1b_2-b_1a_2
\end{matrix}
\right]](/upload/math/4/8/f/48ff379df1c0ffd1a82918295614b029.png)