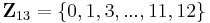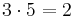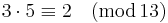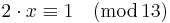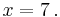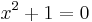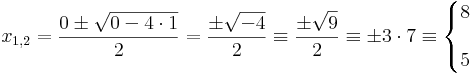Matematika A1a 2008/4. gyakorlat

_{<Matematika A1a 2008}

Bevezetés

Mielőtt a komplex számokra rátérnénk nézzünk példát olyan számkörben való számolásra, mely bár még kommutatív, de eltérést mutat a megszokott számkörökben történő számolástól.

Legyen Z₁₃ az egész számok 13-mal történő osztása maradékainak halmaza. Eszerint a fenti halmaz lényegében a következő:

$\mathbf{Z}_{13}=\{0,1,3,...,11,12\}\,$

Például Z₁₃-ban

$3\cdot 5=2\,$

abban az értelemben, hogy 13-mal 3-mat maradékul adót 5-öt maradékul adóval szorozva 2-t maradékul adót kapunk. Azért a félreértések elkerülése érdekében a fenti egyenlőséget így jelöljük:

$3\cdot 5\equiv 2\quad(\mathrm{mod}\,13)\,$

Vagy egy másik érdekes példa: milyen x Z₁₃-beli esetén lesz

$2\cdot x\equiv 1\quad(\mathrm{mod}\,13)\,$

Világos, hogy ez nem az 1/2, mert az nem egész. Csak 13 lehetőséget kell kipróbálnunk, hogy megtudjuk, van-e és ha igen, mi lesz:

$x=7\,.$

1. Feladat. Oldjuk meg Z₁₃-ban a következő egyenletet:

$x^2+1=0\,$

Megoldás. Ez egy másodfokú egyenlet (és a számkör egy kommutatív test, ahol használható a megoldóképlet), így:

$x_{1,2}=\frac{0\pm \sqrt{0-4\cdot 1}}{2}=\frac{\pm\sqrt{-4}}{2}\equiv\frac{\pm\sqrt{9}}{2}\equiv\pm 3\cdot 7\equiv\left\{\begin{matrix}8\\ \\ 5 \end{matrix}\right.$

Ellenőrzéssel meggyőződhetünk arról, hogy ezek valóban megoldások. (Megjegyezzük, hogy a fenti gondolatmenet ebben a formájában csak egy intuitív gondolatkísérlet, ám utánagondolva módszertanilag szigorúvá tehető.)