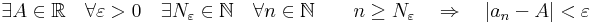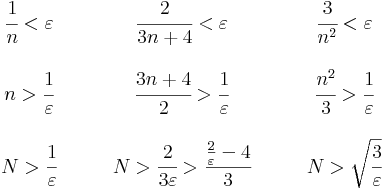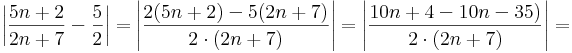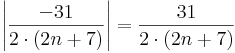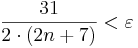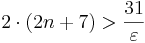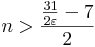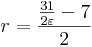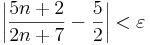Matematika A1a 2008/5. gyakorlat

_{<Matematika A1a 2008}

Definíció – Konvergens sorozat – Azt mondjuk, hogy az (a_n) számsorozat konvergens, ha létezik olyan A ∈ R szám, hogy minden ε pozitív szám esetén megadható olyan N_ε természetes szám, hogy minden az N-nél nagyobb vagy egyenlő n természetes számra |a_n - A| < ε. Illetve szimbolikusan:

$\exists A\in\mathbb{R}\quad\forall\varepsilon>0\quad\exists N_\varepsilon\in\mathbb{N}\quad\forall n\in\mathbb{N}\quad\quad n\geq N_\varepsilon\quad\Rightarrow\quad|a_n-A|<\varepsilon$

Példák. Az 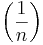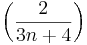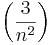$\left(\frac{1}{n}\right)$, $\left(\frac{2}{3n+4}\right)$, $\left(\frac{3}{n^2}\right)$ sorozatok konvergensek.

Ugyanis, Előzetes ismereteink szerint a sorozatok infimuma a 0 és csökkenőek, így A-ra alkalmas értéknek látszik a 0.

Legyen ε > 0. Mindegyikre keresünk olyan N-t, amire teljesül, hogy ha n > N, akkor |a_n| < ε. Rendezve az egyenlőtlenségeket:

$\begin{matrix} \cfrac{1}{n}<\varepsilon \quad\quad & \cfrac{2}{3n+4}<\varepsilon \quad\quad & \cfrac{3}{n^2}<\varepsilon \\ & & \\ n>\cfrac{1}{\varepsilon} \quad\quad & \cfrac{3n+4}{2}>\cfrac{1}{\varepsilon} \quad\quad & \cfrac{n^2}{3}>\cfrac{1}{\varepsilon}\\ & & \\ N>\cfrac{1}{\varepsilon} \quad\quad & N>\cfrac{2}{3\varepsilon}>\cfrac{\frac{2}{\varepsilon}-4}{3} \quad\quad & N>\sqrt{\cfrac{3}{\varepsilon}} \end{matrix}$

Ha tehát N a fenti tulajdonságú, akkor |a_n| < ε mindháromnál teljesül minden n > N-re. Ez pedig azért van, mert minden valós számnál van nagyobb természetes szám (Archimédeszi axióma).

Feladat. Konvergens-e az $a_n=\frac{5n+2}{2n+7}$ általános tagú sorozat?

(Útmutatás: képezzük az |a_n - 5/2| különbséget és becsüljük felül egy 1/n szerű sorozattal, ebből az előző példa gondolatmenetével következtessünk vissza az ε-hoz szükséges N-re.)

Konvergens, ugyanis az A = 5/2 olyan szám, hogy a sorozatnak az A minden környezetén kívül csak véges sok tagja van. A konvergensséget (a definíció alapján) a következőképpen látjuk be. Rögzítsünk tetszőlegesen egy ε pozitív számot. Legyen egyelőre n tetszőleges természetes szám, és vizsgáljuk meg, hogy az |a_n - A| szám felülbecsülhető-e olyan sorozattal, melynek infimuma a 0. A becsléshez

$\left|\frac{5n+2}{2n+7}-\frac{5}{2}\right|=\left|\frac{2(5n+2)-5(2n+7)}{2\cdot(2n+7)}\right|=\left|\frac{10n+4-10n-35)}{2\cdot(2n+7)}\right|=$

$\left|\frac{-31}{2\cdot(2n+7)}\right|=\frac{31}{2\cdot(2n+7)}$

Ahol az utolsó lépésben kapott eredményről kell igazolnunk, hogy egy N indextől kezdve ε-nál kisebb. Ehhez oldjuk meg a

$\frac{31}{2\cdot(2n+7)}<\varepsilon$

egyenlőtlenséget! Reciprokot véve mindkét oldalon (és a reláció érvényességének fenntartására figyelve)

$2\cdot(2n+7)>\frac{31}{\varepsilon}$

$n>\frac{\frac{31}{2\varepsilon}-7}{2}$

Azt kaptuk tehát, hogy minden n-re, mely nagyobb az

$r=\frac{\frac{31}{2\varepsilon}-7}{2}$

számnál, teljesül a kívánt ε-ra vonatkozó egyenlőtlenség. Azaz N-et választhatjuk akármilyen, az r valós számnál nagyobb természetes számra, mert akkor az n > N természetes számokra biztosan igaz lesz a kívánt egyenlőtlenség. r-nél nagyobb N természetes szám pedig van, mert minden valós számnál van nagyobb természetes szám. Tehát összefoglalva, tetszőleges ε pozitív számra, ha

$n>N=\left[\frac{\frac{31}{2\varepsilon}-7}{2}\right]$,

ahol [.] jelöli az „egészrész”t, akkor

$\left|\frac{5n+2}{2n+7}-\frac{5}{2}\right|<\varepsilon$

Megjegyzés. Némiképp indoklásra szorul, hogy honnan az 5/2. Egyrészt később belátjuk, hogy azonos fokszámú polinomok hányadosának határértéke a főegyütthatók hányadosa. Másrészt a sorozat konvergenciájának vizsgálatánál célszerű nagy n értékekre elképzelni mi történik a sorozattal. Ez nem egyszerű dolog, hisz legtöbb esetben a számítás elvégzése nagy nehézséget okoz, valamint naiv elképzeléseink gyakran megcsalhatnak etekinteben (amelyre példát is hozunk később). Ez esetben könnyű kitalálni a megfelelő A számot: helyettesítsünk n helyébe 1.000.000-t. Ekkor a hányados nagyjából 5.000.000 és 2.000.000 hányadosa, azaz 5/2 és ez a közelítés tovább javul, ha n helyébe nagyobb számot gondolunk. Hangsúlyozzuk, hogy más esetekben elhamarkodott következtetésekre juthatunk a kiszámoláson alapuló módszerrel, melyet nevezhetünk akár naiv módszernek is.