Matematika A1a 2008/6. gyakorlat
Tartalomjegyzék |
Monoton, korlátos sorozatok
A konvergencia alábbi, gyakran alkalmazott, elégséges feltétele a sorozatok monoton tulajdonságát helyezi előtérbe. Mindezekhez elevenítsük fel a monoton sorozat definícióját.
Monoton sorozat
Definíció – Azt mondjuk, hogy az (an) valós számsorozat
- monoton növekvő, ha minden n természetes számra teljesül:
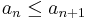
- szigorúan monoton növekvő, ha minden n természetes számra teljesül:
- monoton csökkenő vagy monoton fogyó, ha minden n természetes számra teljesül:
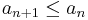
- szigorúan monoton csökkenő, ha minden n természetes számra teljesül:
- monoton, ha monoton növekvő vagy monoton csökkenő
- szigorúan monoton, ha szigorúan monoton növekvő vagy szigorúan monoton csökkenő
Megjegyzés. A monotonitást, például a szigorú monoton növekedést még úgy is megfogalmazhatjuk, hogy tetszőleges n > m természetes számokra: an > am
Feladat. Igazoljuk, hogy az
általános tagú sorozatot szigorúan monoton csökken!
(Útmutatás: használjuk fel, hogy a sin függvény a (0,π/2) intervallumon szigorúan monoton nő.)
Világos:
ezért reciprokot véve
és mivel a sin függvény a (-π/2;+π/2) intervallumon szigorúan monoton növekszik, ezért a fenti egyenlőtlenséget megtartja:
Tétel – a konvergencia monoton korlátossággal megfogalmazott elégséges feltétele – Monoton, korlátos sorozat konvergens.
Megjegyzés. A konvergencia lokalitásából következik, hogy a tétel állítása olyan korlátos sorozatokra is érvényes, melyek csak egy indextől kezdve monotonak.
Bizonyítás. Legyen (an) monoton, korlátos valós számsorozat. Az általánosság megszorítása nélkül feltehető, hogy az (an) monoton növekvő. Világos, hogy a sorozat szuprémuma véges. Belátjuk, hogy a sorozat konvergál a sup(an) számhoz.
Legyen ε > 0 tetszőleges. Ekkor a szuprémum egyenlőtlenségekkel történő jellemzése alapján sup(an)–ε már nem felső korlátja (an)-nek, így létezik N természetes szám, hogy
Mivel (an) monoton növekvő, ezért minden n > N természetes számra
így minden n > N-re
ami azt jelenti, hogy az N+1 indextől kezdve a sorozat minden tagja benne van a sup(an) szám ε sugarú környezetében.
Rendőr elv
Tétel – Közrefogási elv – Ha (an) illetve (bn) az A számhoz konvergáló sorozatok, és (cn) olyan sorozat, hogy egy N természetes számtól kezdve minden n-re
akkor (cn) is konvergens és határértéke A.
Nevezetes határértékek
Állítás – Ha 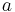 > 0, akkor
> 0, akkor ![\lim\left(\sqrt[n]{a}\,\right)=1](/upload/math/c/a/d/cad48fd4370062236ea8595b4bc052a7.png)
Állítás ![\lim\left(\sqrt[n]{n}\,\right)=1](/upload/math/a/7/7/a77ed16425cb985902fb9369414b1c36.png)
Állítás – Ha pn > 0 általános tagú sorozat polinomrendű, azaz létezik k természetes szám és A pozitív szám, hogy
akkor
1. Konvergens-e az alábbi sorozat és ha igen, adjuk meg a határértékét!
(Útmutatás: közvetlenül rendőrelvvel, vagy a polinom n-edik gyökének határértékére vonatkozó állítással.)
2. Konvergens-e az alábbi sorozat és ha igen, adjuk meg a határértékét!
(Útmutatás: a legmagasabb fokú tag felével becsüljük felül (vagy alul, ha kell) a kisebb fokú tagokat, majd alkalmazzuk a rendőrelvet.)
Itt ![\scriptstyle{\left(\sqrt[n^4]{n^4}\right)}](/upload/math/e/f/b/efba4c08f17d0f3d21646f121b165759.png) az
az ![\scriptstyle{\left(\sqrt[n]{n}\right)}](/upload/math/6/f/8/6f81b1f345ff5049f5122ce8d1e62fe7.png) sorozat
sorozat 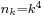 indexsorozattal képezett részsorozata, így az 1-hez tart.
indexsorozattal képezett részsorozata, így az 1-hez tart.
Ahol felhasználtuk, az előző egyenlőtlenség végén kiszámolt határértéket.
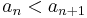
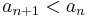
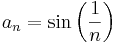
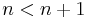
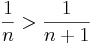
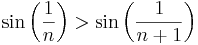
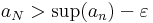
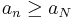
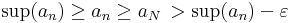
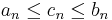
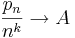
![\lim\left(\sqrt[n]{p_n}\,\right)=1](/upload/math/d/f/c/dfc5922d6010b85811cf6cffe8b40597.png)
![\sqrt[n]{n^2+2n+4}](/upload/math/c/a/6/ca6dbcd6faa4d83237c5565b9c3e8097.png)
![\sqrt[n]{n^2+2n+4}\underset{\scriptstyle{1\leq n\leq n^2}}{\leq}\sqrt[n]{n^2+2n^2+4n^2}=\sqrt[n]{7n^2}=\sqrt[n]{7}\cdot\sqrt[n]{n^2}=\underset{\underset{1}{\downarrow}}{\underbrace{\sqrt[n]{7}}}\cdot\underset{\underset{1}{\downarrow}}{\underbrace{\left(\sqrt[n]{n}\right)^2}}\to 1](/upload/math/5/9/1/591cda753d7dc455dc3203ce706f62cb.png)
![\sqrt[n]{n^2+2n+4}\geq\sqrt[n]{4}\to 1](/upload/math/d/d/1/dd1747643a169b478678e5664c60763e.png)
![\sqrt[n^4]{n^3-3n}](/upload/math/b/6/7/b67cdd587c82e92ffc8c4ce0e5ec5143.png)
![\sqrt[n^4]{n^3-3n}\leq\sqrt[n^4]{n^3}=\underset{\underset{1}{\downarrow}}{\underbrace{\left(\sqrt[n^4]{n^4}\right)}}\,^{\frac{3}{4}}\to 1](/upload/math/b/e/a/bea4e10753dc5886d03158314c894e1e.png)
![\sqrt[n^4]{n^3-3n}\underset{ \underset{\scriptstyle{(n>2)}}{3n\leq\frac{n^3}{2}} }{\geq}\sqrt[n^4]{n^3-\cfrac{n^3}{2}}=\sqrt[n^4]{\frac{n^3}{2}}=\sqrt[n^4]{\frac{1}{2}}\cdot\sqrt[n^4]{n^3}\to 1\cdot 1=1](/upload/math/2/9/e/29ea7e20f6638ed6d2a9bef373c8f2c4.png)