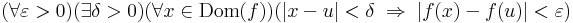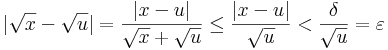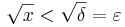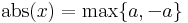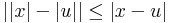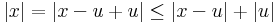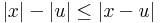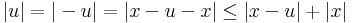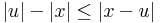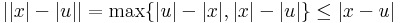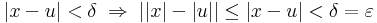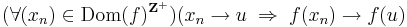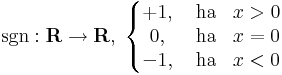|
|
| 1. sor: |
1. sor: |
| | <sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub> | | <sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub> |
| | | | |
| − | ==Végtelen határérték==
| |
| | | | |
| − | Ehhez először definiálnunk kell a végtelen környezeteit.
| |
| − |
| |
| − | '''Definíció.''' Tetszőleges ε>0 számra az ( 1/ε , +∞ ) nyílt intervallumokat a +∞ ε sugarú kipontozott környezetének tekintjük és B<sub>ε</sub>(+∞)-vel jelöljük. Ugyanígy tetszőleges ε>0 számra az ( -∞ , -1/ε) nyílt intervallum a -∞ elem ε sugarú kipontozott környezetének tekintendő és B<sub>ε</sub>(-∞)-vel jelöljük.
| |
| − |
| |
| − | A valós számok halmazát az -∞ +∞ "ideális" elemekkel kibővítve
| |
| − | :<math>\overline{\mathbf{R}}\, </math>
| |
| − | jelöli. Ebben értelmes a sorozathatárérték definíciója a következő formában:
| |
| − |
| |
| − | '''Definíció.''' Legyen ''A'' ∈ '''R''' U {+∞,-∞} és (''a''<sub>n</sub>) egy '''R'''-ben haladó sorozat. Azt mondjuk, hogy az ''A'' határértéke az (''a''<sub>n</sub>)-nek (ekkor ''A'' = +∞ vagy -∞ esetén a konvergencia helyett a divergencia szót használjuk), ha
| |
| − | :tetszőleges ε>0 számra az létezik ''N'' természetes szám, hogy minden ''N''-nél nagyobb ''n'' természetes számra
| |
| − | ::<math>a_n\in \mathrm{B}_{\varepsilon}(A)</math>
| |
| − |
| |
| − | Ekkor ''A'' az egyetlen ilyen és ezt lim(''a''<sub>n</sub>)-nel jelöljük.
| |
| − |
| |
| − | ===Határozatlan esetek===
| |
| − | Konvergens sorozatok esetén láttuk, hogy a határértékképzés felcserélhető a sorozatokkal végzett műveletek elvégzésére, azaz ha * egy alapművelet és
| |
| − | # ''a''<sub>n</sub> <math>\to</math> ''a'' ∈ '''R''' és ''b''<sub>n</sub> <math>\to</math> ''b'' ∈ '''R''',
| |
| − | # (''a''<sub>n</sub> * ''b''<sub>n</sub>) értelmezett és
| |
| − | # ''a'' * ''b'' is értelmezett,
| |
| − | akkor ''a''<sub>n</sub> * ''b''<sub>n</sub> <math>\to</math> ''a'' * ''b''.
| |
| − |
| |
| − | Az alapműveletek között csak a nullával való osztás nincs értelmezve. Ez az előzőek fényében azt jelenti, hogy például a fenti tétel nem alkalmazható az alábbi példára:
| |
| − | # ''a''<sub>n</sub> <math>\equiv</math> 1 <math>\to</math> 1 és ''b''<sub>n</sub> = 1/n <math>\to</math> 0,
| |
| − | # ''a''<sub>n</sub>/''b''<sub>n</sub> <math>\equiv</math> 1/(1/n) értelmezett, de
| |
| − | # 1/0 nem értelmezett
| |
| − | és nem is konvergens a hányadossorozat, bár a határértéke a plusz végtelen.
| |
| − |
| |
| − | Nem mondhatjuk azonban, hogy az 1/0 alakú határértéket mutató sorozatok határértéke mindig a +∞, hiszen az 1/(-1/n) sorozat ugyanilyen módon keletkezett, de a -∞-be tart. Ezt csak abban az esetben mondhatnánk, ha minden ''a''<sub>n</sub> <math>\to</math> 1, és ''b''<sub>n</sub> <math>\to</math> 0 sorozat esetén ''a''<sub>n</sub>/''b''<sub>n</sub> <math>\to</math> +∞ lenne, feltéve, hogy a sorozatok hányadosa létezik.
| |
| − |
| |
| − | Ezt a gondolatot fogjuk használni a végtelen határértékű sorozatokkal végzett műveletekre vonatkozó állítás megfogalmazásánál:
| |
| − | :Ha ''A'' és ''B'' valamelyike a +∞ vagy -∞ szimbólum (a másik, ha nem ilyen, akkor valós szám), akkor az ''A'' * ''B'' alapműveletet akkor értelmezzük a ''C'' szimbólumként (mely szintén vagy valós szám, vagy a +∞, -∞ egyike), ha ''minden'', az ''A''-hoz tartó (''a''<sub>n</sub>) sorozatra és ''minden'', a ''B''-hez tartó (''b''<sub>n</sub>) sorozatra az (''a''<sub>n</sub> * ''b''<sub>n</sub>) sorozat ''szükségszerűen'' a ''C''-hez tart. Ekkor mondjuk tehát, hogy az
| |
| − | ::''A'' * ''B'' = ''C''
| |
| − | :definíció jó.
| |
| − | Például a (+∞) + (+∞) művelet feltétlenül értelmezett és értéke a +∞, mert könnyen látható, hogy ''bármely'' két, a +∞-hez tartó sorozat összege is a +∞-hez tart. Ellenben például a 0<math>\cdot</math>(+∞) művelet nem értelmezhető, mert van két sorozatpár, mely ilyen alakú, de a szorzatuk máshoz tart: (1/n) <math>\cdot</math> n <math>\to</math> 1, de (1/n) <math>\cdot</math> n<sup>2</sup> <math>\to</math> +∞.
| |
| − |
| |
| − | '''Definíció''' – ''Végtelen értékek és alapműveletek'' – Az alábbi műveleti szabályokat vezetjük be a +∞, -∞ szimbólumokra vonatkozóan, az alábbiakban ''r'' tetszőleges valós szám, ''p'' tetszőleges ''pozitív'' szám:
| |
| − | # <math>(\pm\infty)+(\pm\infty)=\pm\infty, \quad\quad(\pm\infty)+r=\pm\infty </math>,
| |
| − | # <math>(\pm\infty)-(\mp\infty)=\pm\infty, \quad\quad(\pm\infty)-r=\pm\infty, \quad\quad r-(\pm\infty)=\mp\infty</math>,
| |
| − | # <math>(\pm\infty)\cdot(\pm\infty)=+\infty, \quad\quad (+\infty)\cdot(-\infty)=-\infty, \quad\quad (\pm\infty)\cdot (\pm p)=+\infty, \quad\quad (\pm\infty)\cdot (\mp p)=-\infty</math>,
| |
| − | # <math>\frac{r}{\pm \infty}=0 \quad\quad \frac{\pm \infty}{\pm p}=+\infty, \quad\quad \frac{\pm \infty}{\mp p}=-\infty</math>,
| |
| − | és a szorzás és az összeadás kommutatív.
| |
| − |
| |
| − |
| |
| − | '''Definíció''' – ''Határozatlan esetek'' – Az alábbi alapműveletek nem értelmezhetők:
| |
| − | # <math>(\pm\infty)-(\pm\infty)</math>,
| |
| − | # <math>0\cdot(\pm\infty), \quad\quad (\pm\infty)\cdot 0</math>,
| |
| − | # <math>\frac{\pm\infty}{\pm \infty}, \quad\quad \frac{\pm\infty}{\mp \infty}, \quad\quad \left(\;\frac{r}{0}\;\right)</math>.
| |
| − |
| |
| − |
| |
| − | Továbbá értelmezhetjük a 0+ és 0- értékeket és a velük való műveletvégzést úgy, hogy
| |
| − | ''a''<sub>n</sub> <math>\to</math> 0+ kifejezésen azt értjük, hogy az (''a''<sub>n</sub>) sorozat egy indextől kezdve pozitív értékeket vesz fel és határértéke a 0, valamint a ''b''<sub>n</sub> <math>\to</math> 0+ kifejezésen azt értjük, hogy az (''a''<sub>n</sub>) sorozat egy indextől kezdve negatív értékeket vesz fel és határértéke a 0. Ekkor minden művelet azt, ami a 0-ra vonatkozik ugyanaz, valamint értelmezhető az alábbi művelet:
| |
| − | :<math>\frac{p}{0\pm}=\pm\infty, \quad\quad \frac{-p}{0\pm}=\mp\infty,</math>.
| |
| − | de 0/0+ és 0/0- természetesen itt sincs.
| |
| − |
| |
| − | '''Tétel''' – ''Végtelen határérték és alapműveletek, a fenti definíciók jók'' – Ha az (''a''<sub>n</sub>) és (''b''<sub>n</sub>) sorozatoknak létezik határértéke, az (''a''<sub>n</sub> * ''b''<sub>n</sub>) sorozat létezik a * alapművelettel és a lim(''a''<sub>n</sub>) * lim(''b''<sub>n</sub>) alapművelet elvégezhető, akkor az (''a''<sub>n</sub> * ''b''<sub>n</sub>) sorozatnak is van határértéke és ez:
| |
| − | :<math> \lim(a_n\,\mbox{*}\, b_n)=\lim(a_n)\,\mbox{*}\, \lim(b_n) \,</math>
| |
| − | Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, a műveletsorozatok határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
| |
| − |
| |
| − | A hatványozással kapcsoltban is vannak határozatlan esetek, ilyen az
| |
| − | :<math>1^{\infty},\quad\quad 0^0,\quad\quad \infty^0</math>
| |
| − | alakú határértékek. Az elsőre példa az Euler-féle határérték, a harmadikra a pozitív szám n-edik gyökökeiből álló sorozat határértéke.
| |
| − |
| |
| − | '''1. feladat.''' Konvergensek-e az alábbi sorozatok? Ha van, mi a határértékük?
| |
| − | : <math>\left(1+\frac{1}{n^2}\right)^{n}, \quad\quad \left(1+\frac{1}{n}\right)^{n^2}</math>
| |
| − | ''(Útmutatás: Alakítsuk át nevezetes alakúvá őket és használjuk a rendőrelvet illetve a majoráns kritériumot.)''
| |
| − |
| |
| − | :<math>
| |
| − | \left(1+\frac{1}{n^2}\right)^{n}=\left(\left(1+\frac{1}{n^2}\right)^{n^2}\right)^{\frac{1}{n}}=\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }
| |
| − | </math>
| |
| − | itt a gyök alatti sorozat az e-hez tart mert a nevezetes sorozat ''n''<sub>''k''</sub> = ''k''<sup>2</sup> indexsorozattal adott részsorozata. Tudjuk, hogy a gyök alatti sorozatnak a 4 felső korlátjam így a rendőrelvvel:
| |
| − | :<math>
| |
| − | 1\leftarrow\sqrt[n]{1}\leq\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }\leq\sqrt[n]{4}\to 1
| |
| − | </math>
| |
| − | Tehát a sorozat az 1-hez tart.
| |
| − |
| |
| − | A másik sorozat esetén az átalakítás:
| |
| − | :<math>
| |
| − | \left(1+\frac{1}{n}\right)^{n^2}=\left(\left(1+\frac{1}{n}\right)^{n}\right)^n
| |
| − | </math>
| |
| − | itt a gyök alatti sorozat az e-hez tart emiatt egy indextől kezdve egy 1-nél nagyobb konstanssal alulbecsülhető. Ugyanis 2-höz (pontosabban az ''ε'' = (e–2)-höz) létezik ''N'', hogy minden ''n'' > ''N''-re a sorozat tagjai nagyobbak 2-nél.
| |
| − | :<math>
| |
| − | +\infty\leftarrow 2^n\leq\left(\left(1+\frac{1}{n}\right)^{n}\right)^n
| |
| − | </math>
| |
| − | Tehát ez a sorozat nem konvergens, de a +∞-hez tart.
| |
| − |
| |
| − |
| |
| − | '''2. feladat.''' Konvergense-e az alábbi sorozat? Ha van, mi a határértéke?
| |
| − | : <math>\left(\frac{n^2-7}{n^2+2n}\right)^{n^2}</math>
| |
| − | ''(Útmutatás: Alakítsuk át nevezetes alakúvá.)''
| |
| − |
| |
| − | :<math>
| |
| − | \left(\frac{n^2+2n}{n^2-7}\right)^{n^2}=\left(\frac{ \cfrac{n^2+2n}{n^2} }{ \cfrac{n^2-7}{n^2} }\right)^{n^2}=\frac{ \left(1+ \cfrac{2}{n}\right)^{n^2} }{ \left(1+ \cfrac{-7}{n^2} \right)^{n^2} }\to +\infty
| |
| − |
| |
| − | </math>
| |
| − | A határértékek indoklása az előző feladat megoldásában lévőhöz hasonló.
| |
| | ==Pontbeli folytonosság== | | ==Pontbeli folytonosság== |
| | | | |
Folytonos egy függvény, ha az értelmezési tartománya minden pontjában folytonos.
tehát az ε-hoz a δ=ε/(\|u)-t kell választanunk.
Ebből kapjuk azt a rendkívül hasznos eszközt, mellyel a nemfolytonosságot jellemezni tudjuk:
Nem folytonos a 0-ban.
nem folytonos a 0-ban.
Emiatt minden polinomfüggvény és racionális törtfüggvény folytonos.
A feltételek nem hagyhatók el. Pl. sin periodikus és így nem injektív, bár folytonos. Pl. sgn(x)(|x|+1) szig. mon. nő, de nem folytonos.
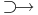 R függvény folytonos az értelmezési tartománya egy u pontjában, ha
R függvény folytonos az értelmezési tartománya egy u pontjában, ha

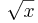 folytonos.
folytonos.
 |x| folytonos. Ezt azzal látjuk be, hogy az abszolútérték következő megadását tekintjük:
|x| folytonos. Ezt azzal látjuk be, hogy az abszolútérték következő megadását tekintjük:
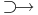 R függvény folytonos az értelmezési tartománya egy u pontjában, ha
R függvény folytonos az értelmezési tartománya egy u pontjában, ha
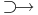 R függvény nem folytonos az értelmezési tartománya egy u pontjában, ha
R függvény nem folytonos az értelmezési tartománya egy u pontjában, ha
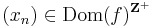 sorozat, hogy bár
sorozat, hogy bár  , de
, de 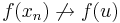 .
.
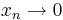 a pozitívok felől, de
a pozitívok felől, de
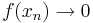 ).
).
 R injektív és folytonos, akkor f szigorúan monoton.
R injektív és folytonos, akkor f szigorúan monoton.