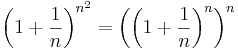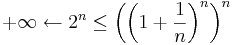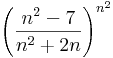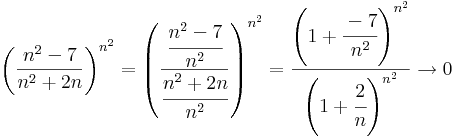Matematika A1a 2008/7. gyakorlat
1. feladat. Konvergensek-e az alábbi sorozatok? Ha van, mi a határértékük?
(Útmutatás: Alakítsuk át nevezetes alakúvá őket és használjuk a rendőrelvet illetve a majoráns kritériumot.)
itt a gyök alatti sorozat az e-hez tart mert a nevezetes sorozat nk = k2 indexsorozattal adott részsorozata. Tudjuk, hogy a gyök alatti sorozatnak a 4 felső korlátjam így a rendőrelvvel:
Tehát a sorozat az 1-hez tart.
A másik sorozat esetén az átalakítás:
itt a gyök alatti sorozat az e-hez tart emiatt egy indextől kezdve egy 1-nél nagyobb konstanssal alulbecsülhető. Ugyanis 2-höz (pontosabban az ε = (e–2)-höz) létezik N, hogy minden n > N-re a sorozat tagjai nagyobbak 2-nél.
Tehát ez a sorozat nem konvergens, de a +∞-hez tart.
2. feladat. Konvergense-e az alábbi sorozat? Ha van, mi a határértéke?
(Útmutatás: Alakítsuk át nevezetes alakúvá.)
A határértékek indoklása az előző feladat megoldásában lévőhöz hasonló.
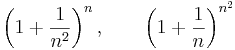
![\left(1+\frac{1}{n^2}\right)^{n}=\left(\left(1+\frac{1}{n^2}\right)^{n^2}\right)^{\frac{1}{n}}=\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }](/upload/math/4/f/d/4fdd89da8789f25184f9172782aa1794.png)
![1\leftarrow\sqrt[n]{1}\leq\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }\leq\sqrt[n]{4}\to 1](/upload/math/a/0/b/a0b8956f5b4ec365555b22e034ed852e.png)