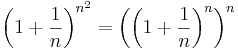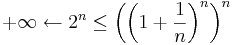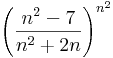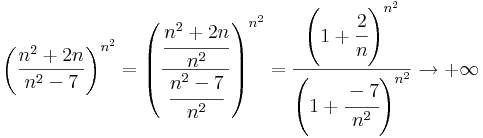Matematika A1a 2008/7. gyakorlat
Végtelen határérték
Ehhez először definiálnunk kell a végtelen környezeteit.
Definíció. Tetszőleges ε>0 számra az ( 1/ε , +∞ ) nyílt intervallumokat a +∞ ε sugarú kipontozott környezetének tekintjük és Bε(+∞)-vel jelöljük. Ugyanígy tetszőleges ε>0 számra az ( -∞ , -1/ε) nyílt intervallum a -∞ elem ε sugarú kipontozott környezetének tekintendő és Bε(-∞)-vel jelöljük.
A valós számok halmazát az -∞ +∞ "ideális" elemekkel kibővítve
jelöli. Ebben értelmes a sorozathatárérték definíciója a következő formában:
Definíció. Legyen A ∈ R U {+∞,-∞} és (an) egy R-ben haladó sorozat. Azt mondjuk, hogy az A határértéke az (an)-nek (ekkor A = +∞ vagy -∞ esetén a konvergencia helyett a divergencia szót használjuk), ha
- tetszőleges ε>0 számra az létezik N természetes szám, hogy minden N-nél nagyobb n természetes számra
Ekkor A az egyetlen ilyen és ezt lim(an)-nel jelöljük.
Határozatlan esetek
Konvergens sorozatok esetén láttuk, hogy a határértékképzés felcserélhető a sorozatokkal végzett műveletek elvégzésére, azaz ha * egy alapművelet és
- an
 a ∈ R és bn
a ∈ R és bn  b ∈ R,
b ∈ R,
- (an * bn) értelmezett és
- a * b is értelmezett,
akkor an * bn  a * b.
a * b.
Az alapműveletek között csak a nullával való osztás nincs értelmezve. Ez az előzőek fényében azt jelenti, hogy például a fenti tétel nem alkalmazható az alábbi példára:
- an
 1
1  1 és bn = 1/n
1 és bn = 1/n  0,
0,
- an/bn
 1/(1/n) értelmezett, de
1/(1/n) értelmezett, de
- 1/0 nem értelmezett
és nem is konvergens a hányadossorozat, bár a határértéke a plusz végtelen.
Nem mondhatjuk azonban, hogy az 1/0 alakú határértéket mutató sorozatok határértéke mindig a +∞, hiszen az 1/(-1/n) sorozat ugyanilyen módon keletkezett, de a -∞-be tart. Ezt csak abban az esetben mondhatnánk, ha minden an  1, és bn
1, és bn  0 sorozat esetén an/bn
0 sorozat esetén an/bn  +∞ lenne, feltéve, hogy a sorozatok hányadosa létezik.
+∞ lenne, feltéve, hogy a sorozatok hányadosa létezik.
Ezt a gondolatot fogjuk használni a végtelen határértékű sorozatokkal végzett műveletekre vonatkozó állítás megfogalmazásánál:
- Ha A és B valamelyike a +∞ vagy -∞ szimbólum (a másik, ha nem ilyen, akkor valós szám), akkor az A * B alapműveletet akkor értelmezzük a C szimbólumként (mely szintén vagy valós szám, vagy a +∞, -∞ egyike), ha minden, az A-hoz tartó (an) sorozatra és minden, a B-hez tartó (bn) sorozatra az (an * bn) sorozat szükségszerűen a C-hez tart. Ekkor mondjuk tehát, hogy az
- A * B = C
- definíció jó.
Például a (+∞) + (+∞) művelet feltétlenül értelmezett és értéke a +∞, mert könnyen látható, hogy bármely két, a +∞-hez tartó sorozat összege is a +∞-hez tart. Ellenben például a 0 (+∞) művelet nem értelmezhető, mert van két sorozatpár, mely ilyen alakú, de a szorzatuk máshoz tart: (1/n)
(+∞) művelet nem értelmezhető, mert van két sorozatpár, mely ilyen alakú, de a szorzatuk máshoz tart: (1/n)  n
n  1, de (1/n)
1, de (1/n)  n2
n2  +∞.
+∞.
Definíció – Végtelen értékek és alapműveletek – Az alábbi műveleti szabályokat vezetjük be a +∞, -∞ szimbólumokra vonatkozóan, az alábbiakban r tetszőleges valós szám, p tetszőleges pozitív szám:
-
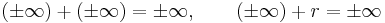 ,
,
-
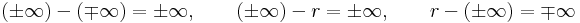 ,
,
-
 ,
,
-
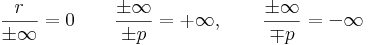 ,
,
és a szorzás és az összeadás kommutatív.
Definíció – Határozatlan esetek – Az alábbi alapműveletek nem értelmezhetők:
-
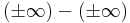 ,
,
-
 ,
,
-
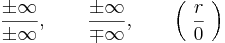 .
.
Továbbá értelmezhetjük a 0+ és 0- értékeket és a velük való műveletvégzést úgy, hogy
an  0+ kifejezésen azt értjük, hogy az (an) sorozat egy indextől kezdve pozitív értékeket vesz fel és határértéke a 0, valamint a bn
0+ kifejezésen azt értjük, hogy az (an) sorozat egy indextől kezdve pozitív értékeket vesz fel és határértéke a 0, valamint a bn  0+ kifejezésen azt értjük, hogy az (an) sorozat egy indextől kezdve negatív értékeket vesz fel és határértéke a 0. Ekkor minden művelet azt, ami a 0-ra vonatkozik ugyanaz, valamint értelmezhető az alábbi művelet:
0+ kifejezésen azt értjük, hogy az (an) sorozat egy indextől kezdve negatív értékeket vesz fel és határértéke a 0. Ekkor minden művelet azt, ami a 0-ra vonatkozik ugyanaz, valamint értelmezhető az alábbi művelet:
 .
.
de 0/0+ és 0/0- természetesen itt sincs.
Tétel – Végtelen határérték és alapműveletek, a fenti definíciók jók – Ha az (an) és (bn) sorozatoknak létezik határértéke, az (an * bn) sorozat létezik a * alapművelettel és a lim(an) * lim(bn) alapművelet elvégezhető, akkor az (an * bn) sorozatnak is van határértéke és ez:
Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, a műveletsorozatok határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
A tétel minden nehézség nélkül bizonyítható, de minden részletre kiterjedő bizonyítása rendkívül hosszadalmas és triviális lépések egymásutánjából áll. Ellenben az olvasó feladata lehet, hogy az összes határozatlan esetre találjon az értelmezhetetlenséget igazoló példát.
1. feladat. Konvergensek-e az alábbi sorozatok? Ha van, mi a határértékük?
(Útmutatás: Alakítsuk át nevezetes alakúvá őket és használjuk a rendőrelvet illetve a majoráns kritériumot.)
itt a gyök alatti sorozat az e-hez tart mert a nevezetes sorozat nk = k2 indexsorozattal adott részsorozata. Tudjuk, hogy a gyök alatti sorozatnak a 4 felső korlátjam így a rendőrelvvel:
Tehát a sorozat az 1-hez tart.
A másik sorozat esetén az átalakítás:
itt a gyök alatti sorozat az e-hez tart emiatt egy indextől kezdve egy 1-nél nagyobb konstanssal alulbecsülhető. Ugyanis 2-höz (pontosabban az ε = (e–2)-höz) létezik N, hogy minden n > N-re a sorozat tagjai nagyobbak 2-nél.
Tehát ez a sorozat nem konvergens, de a +∞-hez tart.
2. feladat. Konvergense-e az alábbi sorozat? Ha van, mi a határértéke?
(Útmutatás: Alakítsuk át nevezetes alakúvá.)
A határértékek indoklása az előző feladat megoldásában lévőhöz hasonló.
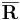
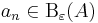
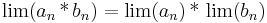
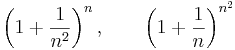
![\left(1+\frac{1}{n^2}\right)^{n}=\left(\left(1+\frac{1}{n^2}\right)^{n^2}\right)^{\frac{1}{n}}=\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }](/upload/math/4/f/d/4fdd89da8789f25184f9172782aa1794.png)
![1\leftarrow\sqrt[n]{1}\leq\sqrt[n]{ \left(1+\frac{1}{n^2}\right)^{n^2} }\leq\sqrt[n]{4}\to 1](/upload/math/a/0/b/a0b8956f5b4ec365555b22e034ed852e.png)