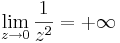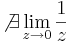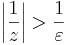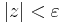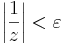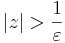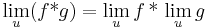Matematika A1a 2008/8. gyakorlat
Mozo (vitalap | szerkesztései) (→Néhány topologikus fogalom) |
Mozo (vitalap | szerkesztései) (→Néhány topologikus fogalom) |
||
| 4. sor: | 4. sor: | ||
*'''torlódási pontjának''' nevezzük, ha minden ''r'' > 0 esetén B<sub>r</sub>(''u'')\{u} ∩ ''A'' nem üres (vagy ekvivalens módon: végtelen) | *'''torlódási pontjának''' nevezzük, ha minden ''r'' > 0 esetén B<sub>r</sub>(''u'')\{u} ∩ ''A'' nem üres (vagy ekvivalens módon: végtelen) | ||
* '''izolált pontjának''' nevezzük, ha ''u'' ∈ ''A'', de nem torlódási pontja ''A''-nak. | * '''izolált pontjának''' nevezzük, ha ''u'' ∈ ''A'', de nem torlódási pontja ''A''-nak. | ||
| + | * '''belső pontjának''' nevezzük, ha van olyan környzete, mely benne van ''A''-ban. | ||
| + | |||
| + | Emellett ''U'' '''nyílt halmaz''', ha minden pontja belső pont és '''zárt''', ha komplementere nyílt. | ||
==Függvényhatárérték=== | ==Függvényhatárérték=== | ||
A lap 2008. október 27., 17:24-kori változata
Néhány topologikus fogalom
Ha A ⊆ R valós számhalmaz, akkor az u ∈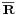 
pontot az A
- torlódási pontjának nevezzük, ha minden r > 0 esetén Br(u)\{u} ∩ A nem üres (vagy ekvivalens módon: végtelen)
- izolált pontjának nevezzük, ha u ∈ A, de nem torlódási pontja A-nak.
- belső pontjának nevezzük, ha van olyan környzete, mely benne van A-ban.
Emellett U nyílt halmaz, ha minden pontja belső pont és zárt, ha komplementere nyílt.
Függvényhatárérték=
Legyen f egy az A ⊆ R halmazon értelmezett, R-be képező függvény. Legyen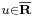 
az A torlódási pontja. Azt mondjuk, hogy az f-nek a 
elem határértéke az u-ban, ha
- minden ε > 0 esetén létezik olyan δ > 0, hogy minden z ∈ A ∩ Bδ(u)\{u}-re f(z) ∈ Bε(v)
ahol természetesen a +∞ és -∞ környezetei a már említett módon értendők.
Feladat. Igazoljuk definíció szerint, hogy
1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| < δ esetén, hogy a függvényérték a ∞ ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
2. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| > 1/δ esetén, hogy a függvényérték a 0-nak ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| > 1/δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
Tétel – Végtelen határérték és alapműveletek – Ha az f és g valós függvényeknek létezik határértékük az 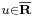helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:
Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
