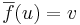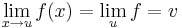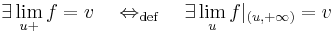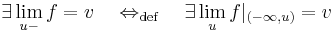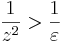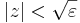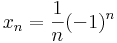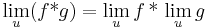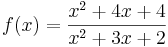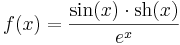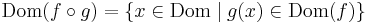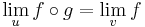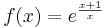Matematika A1a 2008/8. gyakorlat

A MathWikiből
(Változatok közti eltérés)
(→Határérték és függvénykompozíció)
(→Határérték és függvénykompozíció)
85. sor: 85. sor:
 
:<math>f(x)=e^{\frac{x+1}{x}}\,</math>
 
:<math>f(x)=e^{\frac{x+1}{x}}\,</math>
 
függvény határértékeit az értelmezési tartománya határpontjaiban!
 
függvény határértékeit az értelmezési tartománya határpontjaiban!
 +
 +
===Folytonosság és határérték kapcsolta===
 +
A folytonosságot, csak az értelmezési tartomány pontjaiban nézhetünk, hisz a definícióban f(u) is szerepel. Ellenben határértéket akár azon kívüli is nézhetünk (sőt!). Mégis, a két fogalom között szörös kapcsolt van:
 +
 +
'''1. Tétel.''' Legyen az ''u'' az ''f'' értelmezési tartományában. Ekkor a következők ekvivalensek egymással:
 +
# ''f'' folytonos ''u''-ban
 +
# ''u'' izolált pontja Dom(''f'')-nek, vagy ''u'' torlódási pontja Dom(''f'')-nek, létezik ''u''-an határértéke és lim<sub>u</sub>f = f(''u'')
 +
 +
'''2. Tétel.''' Legyen ''u'' a Dom(''f'') véges torlódási pontja és ''v'' véges ('''R'''-beli) szám. Ekkor a következők ekvivalensek.
 +
# <math>\exists\lim\limits_{u}f=v\,</math>
 +
# létezik az ''f''-nek olyan <math>\scriptstyle{\overline{f}}</math> ''u''-ban folytonos kiterjeszétse (vagy módosítása), hogy
 +
#<math>\overline{f}|_{\mathrm{Dom}(f)\setminus \{\u}}=f|_{\mathrm{Dom}(f)\setminus \{\u}}</math> és <math>\overline{f}(u)=v\,</math>
 +
==Szakadási pontok és azok osztályozása==
 
[[Kategória:Matematika A1]]
 
[[Kategória:Matematika A1]]

A lap 2008. október 29., 10:30-kori változata

<Matematika A1a 2008

Tartalomjegyzék

Néhány topologikus fogalom

Ha A ⊆ R valós számhalmaz, akkor az u ∈ 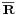\scriptstyle{\overline{\mathbf{R}}} pontot az A

  • torlódási pontjának nevezzük, ha minden r > 0 esetén Br(u)\{u} ∩ A nem üres (vagy ekvivalens módon: végtelen)
  • izolált pontjának nevezzük, ha u ∈ A, de nem torlódási pontja A-nak.
  • belső pontjának nevezzük, ha van olyan környzete, mely benne van A-ban.
  • határpontjának nevezzük, ha torlódási pontja mind a halmaznak, mind a komplementerének.

Emellett U nyílt halmaz, ha minden pontja belső pont és zárt, ha komplementere nyílt.

Például egy nemelfajuló (nem egypontú, nem üres) intervallum végpontjai határpontjai az intervallumnak.

Függvényhatárérték

Legyen f egy az A ⊆ R halmazon értelmezett, R-be képező függvény. Legyen 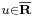\scriptstyle{u\in \overline{\mathbf{R}}} az A torlódási pontja. Azt mondjuk, hogy az f-nek a \scriptstyle{v\in \overline{\mathbf{R}}} elem határértéke az u-ban, ha

minden ε > 0 esetén létezik olyan δ > 0, hogy minden x ∈ A ∩ Bδ(u)\{u}-re f(x) ∈ Bε(v)

ahol természetesen a +∞ és -∞ környezetei a már említett módon értendők.

Ebben az esetben a határérték egyértelmű és jelölése:

\lim\limits_{x\to u}f(x)=\lim\limits_{u}f=v\,

Bal és jobboldali határérték:

\exists\lim\limits_{u+}f=v\quad\Leftrightarrow_{\mathrm{def}}\quad \exists\lim\limits_{u}f|_{(u,+\infty)}=v
\exists\lim\limits_{u-}f=v\quad\Leftrightarrow_{\mathrm{def}}\quad \exists\lim\limits_{u}f|_{(-\infty,u)}=v

Ugyanúgy, ahogy a folytonosság esetén itt is van átviteli elv:

Tétel. Legyen f egy az A ⊆ R halmazon értelmezett, R-be képező függvény. Legyen 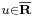\scriptstyle{u\in \overline{\mathbf{R}}} az A torlódási pontja és 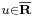\scriptstyle{u\in \overline{\mathbf{R}}}. Ekkor az alábbiak ekvivalensek:

  1. f-nek a v határértéke az u-ban,
  2. minden az A\{u}-ban haladó, az u-hoz konvergáló (xn) sorozat esetén az (f(xn)) a v-hez konvergál.

Ennek a segítségével egy rendkívül hatékony eszközt kapunk arra, hogy a határérték nemlétezését igazoljuk:

Állítás. f-nek pontosan akkor nincs határértéke u-ban, ha van olyan A\{u}-ban haladó, az u-hoz konvergáló (xn) sorozat, mely esetén az az (f(xn)) nem tart egyetlen elemhez sem.

Feladat. Igazoljuk definíció szerint, hogy

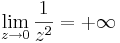
  1. \lim\limits_{z\to 0}\frac{1}{z^2}=+\infty
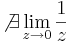  2. \not\exists\lim\limits_{z\to 0}\frac{1}{z} de létezik mindkét egyoldali határértéke.

1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| < δ esetén, hogy a függvényérték a +∞ ε sugarú környezetébe esik, azaz:

\frac{1}{z^2}>\frac{1}{\varepsilon}

Világos, hogy ezt azt jelenti, hogy

|z|<\sqrt{\varepsilon}

amit reciprokvonással kaptunk. Ha tehát δ := négyzetgyök ε és |z| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.

2. Megadunk egy nullsorozatot, mely függvényértékeinek sorozatának semmiképpen nincs határértéke:

x_n=\frac{1}{n}(-1)^n\,

Ekkor x2n \to +∞ és x2n+1 \to -∞, holott ezeknek egyenlőknek kellene lenniők (ha létezik határérték, akkor minden részsorozat határértéke ugyanaz).

Határérték és műveletek

Tétel – Végtelen határérték és alapműveletek – Ha az f és g valós függvényeknek létezik határértékük az 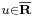\scriptstyle{u\in \overline{\mathbf{R}}} helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:

\lim\limits_u(f\mbox{*}g)=\lim\limits_u f\,\mbox{*}\, \lim\limits_u g \,

Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).

Feladat. Vizsgáljuk meg határérték szempontjából az

f(x)=\frac{x^2+4x+4}{x^2+3x+2}\,

függvényt.

Határérték és rendezés

Két elvet használunk gyakran. Az egyik a "korlátos szor nullához tartó az nullához tart" , a másik a minorálás: ha g(x) az u-ban a + végtelenbe tart és f(x) az u környzetében nagyobb mint g(x), akkor f(x) is a végtelenbe tart.

A rendőr elv megfogalmazása házi feladat.

Feladat. Vizsgáljuk meg, hogy a

f(x)=\frac{\sin(x)\cdot \mathrm{sh}(x)}{e^x}\,

függvénynek létezik-e és ha igen mi a határértéke az értelmezési tartományai határpontjaiban!

Határérték és függvénykompozíció

Definíció. Ha f és g függvények, akkor az f 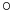\circ g (függvénykompozíció vagy összetett függvény) hozzárendelési utasítása:

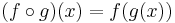(f\circ g)(x)=f(g(x))\, másként: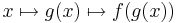 x\mapsto g(x)\mapsto f(g(x))\,

értelmezési tartománya pedig:

\mathrm{Dom}(f\circ g)=\{x\in \mathrm{Dom} \mid g(x)\in \mathrm{Dom}(f)\}

Összetett függvények esetén a leggyakrabban használt, a határértékre vonatkozó állítás:

Tétel. Ha u torlódási pontja a Dom( f 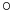\circ g) halmaznak, g injektív az u egy környzetén, létezik határértéke és f-nek létezik határértéke v = limu g-ben, akkor f \circ g-nek is létezik határértéke u-ban és

\lim\limits_{u}f\circ g=\lim\limits_{v}f\,

Feladat. Határozzuk meg az

f(x)=e^{\frac{x+1}{x}}\,

függvény határértékeit az értelmezési tartománya határpontjaiban!

Folytonosság és határérték kapcsolta

A folytonosságot, csak az értelmezési tartomány pontjaiban nézhetünk, hisz a definícióban f(u) is szerepel. Ellenben határértéket akár azon kívüli is nézhetünk (sőt!). Mégis, a két fogalom között szörös kapcsolt van:

1. Tétel. Legyen az u az f értelmezési tartományában. Ekkor a következők ekvivalensek egymással:

  1. f folytonos u-ban
  2. u izolált pontja Dom(f)-nek, vagy u torlódási pontja Dom(f)-nek, létezik u-an határértéke és limuf = f(u)

2. Tétel. Legyen u a Dom(f) véges torlódási pontja és v véges (R-beli) szám. Ekkor a következők ekvivalensek.

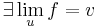
  1. \exists\lim\limits_{u}f=v\,
  2. létezik az f-nek olyan 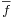\scriptstyle{\overline{f}} u-ban folytonos kiterjeszétse (vagy módosítása), hogy
  3. Értelmezés sikertelen (ismeretlen függvény\u): \overline{f}|_{\mathrm{Dom}(f)\setminus \{\u}}=f|_{\mathrm{Dom}(f)\setminus \{\u}} 
és \overline{f}(u)=v\,

Szakadási pontok és azok osztályozása

A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_A1a_2008/8._gyakorlat&oldid=4385”
Személyes eszközök