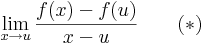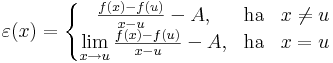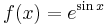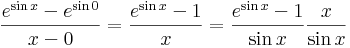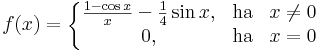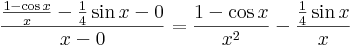Matematika A1a 2008/9. gyakorlat
Mozo (vitalap | szerkesztései) (→Differenciálhatóság) |
Mozo (vitalap | szerkesztései) (→Differenciálhatóság) |
||
| 20. sor: | 20. sor: | ||
ahol ''A'' az ''m''-et jelöli, ha 1)-et tudjuk és 2)-t igazoljuk és lim<sub>x <math>\to</math> u</sub> (f(x)-f(u)/(x-u))-t, ha fordított a helyzet. | ahol ''A'' az ''m''-et jelöli, ha 1)-et tudjuk és 2)-t igazoljuk és lim<sub>x <math>\to</math> u</sub> (f(x)-f(u)/(x-u))-t, ha fordított a helyzet. | ||
| − | Világos, hogy a (*) határérték egy úgy nevezett határozatlan kifejezés, hisz mindig 0/0 alakú. | + | Világos, hogy a (*) határérték egy úgy nevezett határozatlan kifejezés, hisz mindig 0/0 alakú. Ez a a szelők meredekségének határértéke, |
| + | Az első definíció is szemléletes. Itt arról van szó, hogy a függvény felírható ''u'' körül egy lineárisan eltűnő és egy magasabb rendben eltűnű tag összegeként: | ||
| + | :<math>\ell(x)=f(u)+m(x-u)</math>, a lineáris és <math>\varepsilon(x)(x-u)</math> a nemlineáris | ||
'''Példa.''' Igazoljuk, hogy | '''Példa.''' Igazoljuk, hogy | ||
:<math>f(x)=e^{\sin x}\,</math> | :<math>f(x)=e^{\sin x}\,</math> | ||
| 33. sor: | 35. sor: | ||
'''Példa.''' Igazoljuk, hogy | '''Példa.''' Igazoljuk, hogy | ||
| − | :<math>f(x)=\left\{\begin{matrix}\frac{1-\cos x }{x}-\sin x, & \mathrm{ha} & x\ne 0\\ 0, & \mathrm{ha} & x=0\end{matrix}\right.</math> | + | :<math>f(x)=\left\{\begin{matrix}\frac{1-\cos x }{x}-\frac{1}{4}\sin x, & \mathrm{ha} & x\ne 0\\ 0, & \mathrm{ha} & x=0\end{matrix}\right.</math> |
| − | differenciálható a 0-ban és deriváltja 1. | + | differenciálható a 0-ban és deriváltja 1/4. |
''Megoldás.'' Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x≠0. Ekkor | ''Megoldás.'' Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x≠0. Ekkor | ||
:<math> | :<math> | ||
| − | \frac{\frac{1-\cos x }{x}-\sin x -0}{x-0}=\frac{1-\cos x}{x^2}-\frac{\sin x}{x}</math> | + | \frac{\frac{1-\cos x }{x}-\frac{1}{4}\sin x -0}{x-0}=\frac{1-\cos x}{x^2}-\frac{\frac{1}{4}\sin x}{x}</math> |
| − | Ha most ''x'' <math>\to</math> 0, akkor az utolsó egyenlőség után az első tényező és a második | + | Ha most ''x'' <math>\to</math> 0, akkor az utolsó egyenlőség után az első tényező és a második tag, mint nevezetes határérték az 1/2-hez tart, míg a második tag az 1/4-hez. Emiatt a határérték 1/4. |
A lap 2008. november 24., 22:03-kori változata
Differenciálhatóság
Legyen f valós-valós függvény, u ∈ Dom(f)∩Dom(f)'. Az f függvény differenciálható az u pontban, ha
1. Definíció -- létezik olyan ε: Dom(f) 
R függvény és olyan m ∈ R szám, hogy:
- minden x ∈ Dom(f)-re
- f(x) = f(u) + m(x - u) + ε(x)(x - u) és
- ε(u) = 0 és ε az u-ban folytonos.
Ebben az esetben az f függvény u-beli deriváltja m és jele f'(u)
2. Definíció -- létezik és véges a következő határérték:
Ekkor f'(u) maga a fenti határérték.
A két definíció ekvivalens, amit a következő egyenlőséggel lehet igazolni:
ahol A az m-et jelöli, ha 1)-et tudjuk és 2)-t igazoljuk és limx u (f(x)-f(u)/(x-u))-t, ha fordított a helyzet.
Világos, hogy a (*) határérték egy úgy nevezett határozatlan kifejezés, hisz mindig 0/0 alakú. Ez a a szelők meredekségének határértéke,
Az első definíció is szemléletes. Itt arról van szó, hogy a függvény felírható u körül egy lineárisan eltűnő és egy magasabb rendben eltűnű tag összegeként:
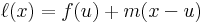, a lineáris és 
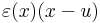a nemlineáris
Példa. Igazoljuk, hogy
differenciálható a 0-ban és deriváltja 1.
Megoldás. Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x≠0. Ekkor
Ha most x 0, akkor az utolsó egyenlőség után az első tényező és a második tényező is az 1-hez tart, minthogy ezek nevezetes határértékek.
Példa. Igazoljuk, hogy
differenciálható a 0-ban és deriváltja 1/4.
Megoldás. Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x≠0. Ekkor
Ha most x 0, akkor az utolsó egyenlőség után az első tényező és a második tag, mint nevezetes határérték az 1/2-hez tart, míg a második tag az 1/4-hez. Emiatt a határérték 1/4.
