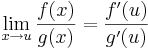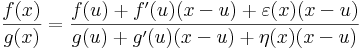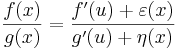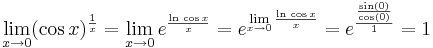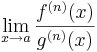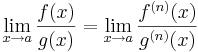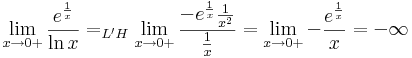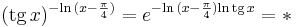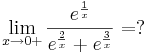Matematika A1a 2008/9. gyakorlat

A MathWikiből

(Változatok közti eltérés)

Ugrás: navigáció, keresés

A lap 2009. április 22., 09:57-kori változata

_{<Matematika A1a 2008}

Differenciálási szabályok

lásd bárhol, pl: http://en.wikibooks.org/wiki/Calculus/Differentiation

.

L'Hospital-szabályok

Tétel -- Gyenge L'Hospital-szabály -- Legyenek f és g: A $\to$ R valós-valós függvények, u ∈ A ∩ A ', f(u)=g(u)=0, mindkettő differenciálható u-ban és g'(u) ≠ 0. Ekkor létezik a lim_u(f/g), és

$\lim\limits_{x\to u}\frac{f(x)}{g(x)}=\frac{f'(u)}{g'(u)}$

Ugyanis,' írjuk fel az 1. definíciónak megfelelően a határértéket. Létezik az u-hoz olyan ε, η: A $\to$ R, hogy minden x ∈ A ∩ Dom(f/g)-ra

$\frac{f(x)}{g(x)}=\frac{f(u)+f'(u)(x-u)+\varepsilon(x)(x-u)}{g(u)+g'(u)(x-u)+\eta(x)(x-u)}$

és ∃lim_uε=ε(u)=0, ∃lim_uη=η(u)=0. Emiatt és f(u)=g(u)=0 miatt

$\frac{f(x)}{g(x)}=\frac{f'(u)+\varepsilon(x)}{g'(u)+\eta(x)}$

Aminek a határéttéke, ha x tart u-hoz a kívánt hányados, amennyiben ellenőrizük, hogy g'(u) + η nem lesz nulla egy elég szűk környzeteben. Ekkor ugyanis a hányadosnak nem lenne értelme. Nos, |η| egy elég kis környzetben a nulla |g'(u)|/2 sugarú környzetében lesz, így ez a veszély nem fenyeget.

1. Feladat. a.

$\lim\limits_{x\to 0} (\cos x)^{\frac{1}{x}}=\lim\limits_{x\to 0} e^{\frac{\mathrm{ln}\,\cos x}{x}}= e^{\lim\limits_{x\to 0}\frac{\mathrm{ln}\,\cos x}{x}}=e^{\frac{\frac{\sin(0)}{\cos (0)}}{1}}=1$

Tétel -- Erős L'Hospital-szabály -- Legyenek f és g: (a,b) $\to$ R az (a,b)-ben differenciálható függvények,

lim_a f=lim_a g=0, vagy ∞,

lim_a f '=lim_a g '=0, vagy ∞,

$\vdots\,$

de lim_a g⁽ⁿ⁾ ≠ 0 és létezzen a

$\lim\limits_{x\to a}\frac{f^{(n)}(x)}{g^{(n)}(x)}$

Ekkor létezik a lim_a(f/g), és

$\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f^{(n)}(x)}{g^{(n)}(x)}$

Bizonyítás a Cauchy-féle középérték tétellel, illetve ennek általánosításával.

1. Feladat. b.

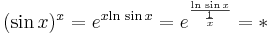
$(\sin x)^{x}= e^{x\mathrm{ln}\,\sin x}= e^{\frac{\mathrm{ln}\,\sin x}{\frac{1}{x}} }=*$

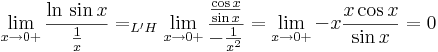
$\lim\limits_{x\to 0+ }\frac{\mathrm{ln}\,\sin x}{\frac{1}{x}} =_{L'H}\lim\limits_{x\to 0+ }\frac{\frac{\cos x}{\sin x}}{-\frac{1}{x^2}}=\lim\limits_{x\to 0+ }-x\frac{x\cos x}{\sin x}=0$

* = e 0 = 1

1. Feladat. c.

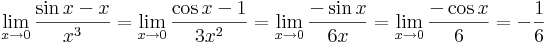
$\lim\limits_{x\to 0}\frac{\sin x-x}{x^3}=\lim\limits_{x\to 0}\frac{\cos x -1}{3x^2}=\lim\limits_{x\to 0}\frac{-\sin x}{6x}=\lim\limits_{x\to 0}\frac{-\cos x}{6}=-\frac{1}{6}$

1. Feladat. d.

$\lim\limits_{x\to 0+}\frac{e^{\frac{1}{x}}}{\mathrm{ln}\,x }=_{L'H} \lim\limits_{x\to 0+} \frac{ -e^{\frac{1}{x}} \frac{1}{x^2 } }{\frac{1}{x}}= \lim\limits_{x\to 0+}-\frac{e^{\frac{1}{x}}}{x}=- \infty$

1. Feladat. e. x $\to$ π/4

$(\mathrm{tg}\, x)^{-\mathrm{ln}\,(x-\frac{\pi}{4})}= e^{-\mathrm{ln}\,(x-\frac{\pi}{4})\mathrm{ln}\,\mathrm{tg}\, x}=*$

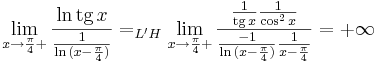
$\lim\limits_{x\to \frac{\pi}{4}+ }\frac{\mathrm{ln}\,\mathrm{tg}\, x}{\frac{1}{\mathrm{ln}\,(x-\frac{\pi}{4})}} =_{L'H}\lim\limits_{x\to \frac{\pi}{4}+ }\frac{ \frac{1}{\mathrm{tg}\, x}\frac{1}{\cos^2 x}}{\frac{-1}{\mathrm{ln}\,(x-\frac{\pi}{4}) }\frac{1}{ x-\frac{\pi}{4}} }=+\infty$

* = 0

1. Feladat. f. -- amikor nem működik az ismételt L'Hospitálás --

$\lim\limits_{x\to 0}\frac{1}{x}-\frac{1}{1-\cos x}=?$

1. Feladat. g. -- amikor nem működik az ismételt L'Hospitálás --

$\lim\limits_{x\to 0+}\frac{e^{\frac{1}{x}}}{e^{\frac{2}{x}}+e^{\frac{3}{x}}}=?$

Fermat-féle szélsőértéktétel

Tétel -- Differenciálható függvény belső pontbeli szélsőértéke létezésének szükséges feltétele -- Ha f valós-valós függvény és f differenciálható az u ∈ int Dom(f) pontban és f-nek u-ban lokális szélsőértéke van, akkor

f'(u) = 0,

Tipikus átvitelielves tétel, hisz a "határérték" létezését tudjuk, csak az értékét kell kiszámolnunk. Tegyük fel, hogy u-ban minimum van. Legyen (δ_n) az 0-hoz tartó pozitív sorozat, mely minden n-re δ_n + u, u- δ_n ∈ Dom(f). Ekkor

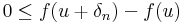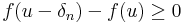
$0\leq f(u+\delta_n)-f(u)\,$ és $f(u-\delta_n)-f(u)\geq 0\,$

Most az elsőt osszuk le &deta;_n-nel, a másodikat -&deta;_n-nel. Ekkor:

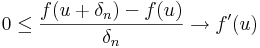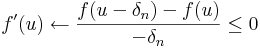
$0\leq\frac{f(u+\delta_n)-f(u)}{\delta_n}\to f'(u)\,$ és $f'(u)\leftarrow\frac{f(u-\delta_n)-f(u)}{-\delta_n}\leq 0\,$

S mivel, ha egy sorozat csupa nemnegatív (nempozitív), akkor a határértéke is ilyen, ezért:

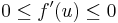$0\leq f'(u)\leq 0\,$ azaz $f'(u)=0\,$

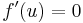
2. Feladat. Igaz-e?

Ha f differenciálható az u ∈ int Dom(f)-ben és f'(u)=0, akkor ott szélsőértéke van.
Ha f differenciálható az u ∈ Dom(f)-ben és ott szélső értéke van, akkor f'(u)=0.
Ha f: [a,b] $\to$ R monoton és létezik f'(b) és = 0, akkor ott lokális szélsőértéke van (itt f'(b)-n a baloldali deriváltat értjük).
Ha f-nek az u ∈ int Dom(f)-ben szélsőértéke van, akkor f'(u)=0.

Megoldás.

Nem igaz. Ellenpélda: f(x)=x³ és u = 0. Itt ugyanis u ∈ int Dom(f), f'(0)=0, de nincs szélsőértéke f-nek. A derivált zárushelye ugyanis nem elégséges feltétele a szélsőértéknek.
Nem igaz. [0,1] zárton az f(x)=x-nek szélsőértéke a 0, de 0-ban a jobboldali derivált 1.
Igaz. Még akkor is, ha f'(b) nem nulla, pusztán a monotonitás következménye.
Nem igaz, mert még az se biztos, hogy létezik a derivált. Ellenpélda: f(x)=|x|, u=0

@@ 1. sor: / 1. sor: @@
 <sub>[[Matematika A1a 2008|<Matematika A1a 2008]]</sub>
-==Differenciálhatóság==
-Legyen ''f'' valós-valós függvény, ''u'' &isin; Dom(''f'')&cap;Dom(''f'')'. Az ''f'' függvény differenciálható az ''u'' pontban, ha
-'''1. Definíció''' -- létezik olyan &epsilon;: Dom(''f'') <math>\to</math> '''R''' függvény és olyan ''m'' &isin; '''R''' szám, hogy:
-# minden ''x'' &isin; Dom(''f'')-re
-#:''f''(''x'') = ''f''(''u'') + ''m''(''x'' - ''u'') + &epsilon;(''x'')(''x'' - ''u'') és
-# &epsilon;(''u'') = 0 és &epsilon; az ''u''-ban folytonos.
-Ebben az esetben az ''f'' függvény ''u''-beli deriváltja ''m'' és jele f'(''u'')
-'''2. Definíció''' -- létezik és véges a következő határérték:
-:<math>\lim\limits_{x\to u}\frac{f(x)-f(u)}{x-u}\quad\quad(*)</math>
-Ekkor f'(''u'') maga a fenti határérték.
-A két definíció ekvivalens, amit a következő egyenlőséggel lehet igazolni:
-:<math>\varepsilon(x)=\left\{\begin{matrix}\frac{f(x)-f(u)}{x-u}-A, & \mathrm{ha} & x\ne u\\
-\lim\limits_{x\to u}\frac{f(x)-f(u)}{x-u}-A, & \mathrm{ha} & x=u\end{matrix}\right.</math>
-ahol ''A'' az ''m''-et jelöli, ha 1)-et tudjuk és 2)-t igazoljuk és lim<sub>x <math>\to</math> u</sub> (f(x)-f(u)/(x-u))-t, ha fordított a helyzet.
-Világos, hogy a (*) határérték egy úgy nevezett határozatlan kifejezés, hisz mindig 0/0 alakú. Ez a  a szelők meredekségének határértéke,
-Az első definíció is szemléletes. Itt arról van szó, hogy a függvény felírható ''u'' körül egy lineárisan eltűnő és egy magasabb rendben eltűnű tag összegeként:
-:<math>\ell(x)=f(u)+m(x-u)</math>, a lineáris és <math>\varepsilon(x)(x-u)</math> a nemlineáris
-'''Példa.''' Igazoljuk, hogy
-:<math>f(x)=e^{\sin x}\,</math>
-differenciálható a 0-ban és deriváltja 1.
-''Megoldás.'' Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x&ne;0. Ekkor
-:<math>
-\frac{e^{\sin x}-e^{\sin 0}}{x-0}=\frac{e^{\sin x}-1}{x}=\frac{e^{\sin x}-1}{\sin x}\frac{x}{\sin x}</math>
-Ha most ''x'' <math>\to</math> 0, akkor az utolsó egyenlőség után az első tényező és a második tényező is az 1-hez tart, minthogy ezek nevezetes határértékek.
-'''Példa.''' Igazoljuk, hogy
-:<math>f(x)=\left\{\begin{matrix}\frac{1-\cos x }{x}-\frac{1}{4}\sin x, & \mathrm{ha} & x\ne 0\\ 0, & \mathrm{ha} & x=0\end{matrix}\right.</math>
-differenciálható a 0-ban és deriváltja 1/4.
-''Megoldás.'' Definíció szerint igazoljuk, azaz a pontbeli derivált (*) képletével. Legyen x&ne;0. Ekkor
-:<math>
-\frac{\frac{1-\cos x }{x}-\frac{1}{4}\sin x -0}{x-0}=\frac{1-\cos x}{x^2}-\frac{\frac{1}{4}\sin x}{x}</math>
-Ha most ''x'' <math>\to</math> 0, akkor az utolsó egyenlőség után az első tényező és a második tag, mint nevezetes határérték az 1/2-hez tart, míg a második tag az 1/4-hez. Emiatt a határérték 1/4.
 ==Differenciálási szabályok==

Matematika A1a 2008/9. gyakorlat

A lap 2009. április 22., 09:57-kori változata

Differenciálási szabályok

L'Hospital-szabályok

Fermat-féle szélsőértéktétel

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök