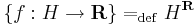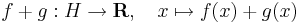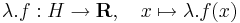Matematika A2a 2008/1. gyakorlat
Mozo (vitalap | szerkesztései) (→Függvénytér) |
Mozo (vitalap | szerkesztései) (→Példák) |
||
| 14. sor: | 14. sor: | ||
:<math>f=\lambda_1</math><math>f_1</math> + <math>\lambda_2</math><math>f_2</math> + ...+ <math> \lambda_n</math><math>f_n</math>, | :<math>f=\lambda_1</math><math>f_1</math> + <math>\lambda_2</math><math>f_2</math> + ...+ <math> \lambda_n</math><math>f_n</math>, | ||
ahol f<sub>1</sub>, ..., f<sub>n</sub> ∈ ''B''. ''B'' elemszáma a dimenzió. | ahol f<sub>1</sub>, ..., f<sub>n</sub> ∈ ''B''. ''B'' elemszáma a dimenzió. | ||
| + | A lineáris tér egy részhalmaza altér, ha zárt az összeadásra és a számmal való szorzásra. | ||
===Példák=== | ===Példák=== | ||
| − | '''1.''' <math>\mathbf{R}^{\mathbf{R}}</math>, melynek elemeit koordinátarendszerben is tudjuk ábrázolni. | + | '''1.''' |
| + | :<math>\mathbf{R}^{\mathbf{R}}</math>, | ||
| + | melynek elemeit koordinátarendszerben is tudjuk ábrázolni. Természetesen ez végtelen dimenziós. | ||
| + | |||
| + | '''2.''' Az intervallumon korlátos függvények B(I) halmaza altere az előzőnek. | ||
| + | |||
| + | '''3.''' A zárt intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b] | ||
| + | |||
| + | '''4.''' | ||
<!-- Az első gyakorlaton a '''R'''<sup>n</sup> topologikus tulajdonságait beszéljük meg, különös tekintettel, az '''R'''<sup>n</sup> egy részhalmazából '''R'''<sup>m</sup>-be ható folytonos leképezésekre. A meghatározottság kedvéért '''R'''<sup>n</sup>-en a | <!-- Az első gyakorlaton a '''R'''<sup>n</sup> topologikus tulajdonságait beszéljük meg, különös tekintettel, az '''R'''<sup>n</sup> egy részhalmazából '''R'''<sup>m</sup>-be ható folytonos leképezésekre. A meghatározottság kedvéért '''R'''<sup>n</sup>-en a | ||
A lap 2010. február 5., 11:29-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Függvénytér
A félév során gyakran fogunk találkozni olyan lineáris terekkel (a lineáris tér fogalmát az előadáson tanuljuk meg), melyek elemi függvények. Ezeknek alaptípusa a következő. Legyen H tetszőleges halmaz. Ekkor a
halmazt, azaz a H-n értelmezett R-be képező függvények halmazát függvénytérnek nevezzük. A függvénytér lineáris tér a pontonként műveletekkel, azaz a következőkkel:
ha λ valós szám, akkor
Függvénytér lineáris alterét is függvénytérnek nevezzük. Lineáris altér egy lineáris tér részhalmaza, ha a fenti műveletekre zárt.
Az F függvénytér B részhalmaza bázis, ha B-beli elemek lineáris kombinációjával a tér összes eleme egyértelműen előáll, azaz ha minden f ∈ F-re léteznek egyértelműen olyan λ1, ..., λn számok, hogy
- f = λ1f1 + λ2f2 + ...+ λnfn,
ahol f1, ..., fn ∈ B. B elemszáma a dimenzió. A lineáris tér egy részhalmaza altér, ha zárt az összeadásra és a számmal való szorzásra.
Példák
1.
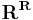 ,
,
melynek elemeit koordinátarendszerben is tudjuk ábrázolni. Természetesen ez végtelen dimenziós.
2. Az intervallumon korlátos függvények B(I) halmaza altere az előzőnek.
3. A zárt intervallumon folytonos függvények C[a,b] tere része az a B[a,b]-nek. Ugyanígy a Riemann integrálható függvények is R[a,b]
4.
| 2. gyakorlat |