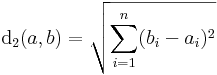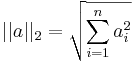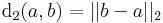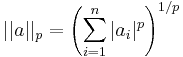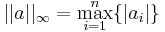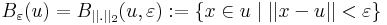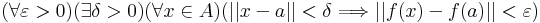Matematika A2a 2008/1. gyakorlat
Mozo (vitalap | szerkesztései) (→Topologikus alapfogalmak) |
Mozo (vitalap | szerkesztései) |
||
| 3. sor: | 3. sor: | ||
:<math>\left\{\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}:x_1,x_2,...,x_n\in \mathbf{R}\right\}</math> | :<math>\left\{\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}:x_1,x_2,...,x_n\in \mathbf{R}\right\}</math> | ||
halmazt, azaz az n emeletes valós értékű oszlopvektorkat értjük. (Mások azt mondanák, hogy '''R''' saját magával vett n-szeres Descartes-szorzata, ami azonban később elfedné a "sorvektor" és az "oszlopvektor" különbséget, ami a lineéris algebra szempontjából nem kerülendő.) | halmazt, azaz az n emeletes valós értékű oszlopvektorkat értjük. (Mások azt mondanák, hogy '''R''' saját magával vett n-szeres Descartes-szorzata, ami azonban később elfedné a "sorvektor" és az "oszlopvektor" különbséget, ami a lineéris algebra szempontjából nem kerülendő.) | ||
| − | + | ||
| − | + | ==Vektorfüggvények ábrázolása== | |
:''Egyelőre görbére és felületre elég a hétköznapi értelemben gondolni. Ezekkel számolni (vonal és felületi intagrál) csak az A3-ba fogunk.'' | :''Egyelőre görbére és felületre elég a hétköznapi értelemben gondolni. Ezekkel számolni (vonal és felületi intagrál) csak az A3-ba fogunk.'' | ||
'''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> függvények két legjellegzetesebb, legjobban szemléltethető típusa az | '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> függvények két legjellegzetesebb, legjobban szemléltethető típusa az | ||
| 27. sor: | 27. sor: | ||
:<math>f:[-2\pi,2\pi]\to\mathbf{R}^3;\quad t\mapsto\begin{pmatrix}1+\cos t\\ \sin t\\ 2\sin\left(\frac{1}{2}t\right)\end{pmatrix}</math> | :<math>f:[-2\pi,2\pi]\to\mathbf{R}^3;\quad t\mapsto\begin{pmatrix}1+\cos t\\ \sin t\\ 2\sin\left(\frac{1}{2}t\right)\end{pmatrix}</math> | ||
függvény által van meghatározva. | függvény által van meghatározva. | ||
| − | + | ==Topologikus alapfogalmak== | |
| + | ===Metrika és norma=== | ||
'''R'''<sup>n</sup>-ben értelmezzük két pont euklidészi távolságát (ez az euklideszi metrika). Ha a és b az '''R'''<sup>n</sup> két tetszőleges pontja, akkor | '''R'''<sup>n</sup>-ben értelmezzük két pont euklidészi távolságát (ez az euklideszi metrika). Ha a és b az '''R'''<sup>n</sup> két tetszőleges pontja, akkor | ||
:<math>\mathrm{d}_2(a,b)=\sqrt{\sum\limits_{i=1}^n(b_i-a_i)^2}</math> | :<math>\mathrm{d}_2(a,b)=\sqrt{\sum\limits_{i=1}^n(b_i-a_i)^2}</math> | ||
| 36. sor: | 37. sor: | ||
Az már a matematikusokra tartozik, hogy absztrakt módon definiálják a metrika és a norma fogalmát és belátják, hogy tetszőleges ''p'' pozitív számra | Az már a matematikusokra tartozik, hogy absztrakt módon definiálják a metrika és a norma fogalmát és belátják, hogy tetszőleges ''p'' pozitív számra | ||
:<math>||a||_p=\left(\sum\limits_{i=1}^{n}|a_i|^p\right)^{1/p}</math> | :<math>||a||_p=\left(\sum\limits_{i=1}^{n}|a_i|^p\right)^{1/p}</math> | ||
| − | szintén norma (p=2-re az euklidészi). | + | szintén norma (p=2-re az euklidészi). Hasznos sokszor a szuprémum vagy maximumnorma is: |
| − | === | + | :<math>||a||_\infty=\max\limits_{i=1}^{n}\{|a_i|\}</math> |
| + | ===Nyílt, zárt és kompakt halmazok=== | ||
| + | Az u ∈ '''R'''<sup>n</sup> pont ε sugarú gömbi környezetén értjük a | ||
| + | :<math>B_\varepsilon(u)=B_{||.||_2}(u,\varepsilon):=\{x\in u\mid ||x-u||<\varepsilon\}</math> | ||
| + | halmazt ||.||<sub>2</sub> az euklideszi normát jelenti, ekkor egy gömb '''R'''<sup>3</sup>-ban tényleg gömb lesz. | ||
| + | ==Folytonosság== | ||
Azt mondjuk, hogy az '''R'''<sup>n</sup> egy ''A'' részhalmazán értelezett és '''R'''<sup>m</sup>-be ható ''f'' leképezés folytonos az értelmezési tartománya egy ''a'' ∈ ''A'' pontjában | Azt mondjuk, hogy az '''R'''<sup>n</sup> egy ''A'' részhalmazán értelezett és '''R'''<sup>m</sup>-be ható ''f'' leképezés folytonos az értelmezési tartománya egy ''a'' ∈ ''A'' pontjában | ||
:<math>(\forall\varepsilon>0)(\exists\delta>0)(\forall x\in A)(||x-a||<\delta\Longrightarrow||f(x)-f(a)||<\varepsilon)</math> | :<math>(\forall\varepsilon>0)(\exists\delta>0)(\forall x\in A)(||x-a||<\delta\Longrightarrow||f(x)-f(a)||<\varepsilon)</math> | ||
A lap 2008. február 2., 21:30-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Az első gyakorlaton a Rn topologikus tulajdonságait beszéljük meg, különös tekintettel, az Rn egy részhalmazából Rm-be ható folytonos leképezésekre. A meghatározottság kedvéért Rn-en a
halmazt, azaz az n emeletes valós értékű oszlopvektorkat értjük. (Mások azt mondanák, hogy R saját magával vett n-szeres Descartes-szorzata, ami azonban később elfedné a "sorvektor" és az "oszlopvektor" különbséget, ami a lineéris algebra szempontjából nem kerülendő.)
Tartalomjegyzék |
Vektorfüggvények ábrázolása
- Egyelőre görbére és felületre elég a hétköznapi értelemben gondolni. Ezekkel számolni (vonal és felületi intagrál) csak az A3-ba fogunk.
Rn  Rm függvények két legjellegzetesebb, legjobban szemléltethető típusa az
Rm függvények két legjellegzetesebb, legjobban szemléltethető típusa az
- R2
 R típusú felületek (kétváltozós, számértékű) és az
R típusú felületek (kétváltozós, számértékű) és az
- R
 R3 típusú tér- vagy R
R3 típusú tér- vagy R  R2 típusú síkgörbék (egyváltozós, vektorértékű).
R2 típusú síkgörbék (egyváltozós, vektorértékű).
Persze ezek is csak akkor személetesek, ha viszonlag egyszerűek (mondjuk polinomiálisak vagy elemi függvényekből vannak összerakva) vagy kevéssé változtatják a függvényérékeiket (simák).
1) Példa R2  R ábrázolására az
R ábrázolására az
egyenletű majomnyereg felület:
Itt az [xy] sík minden egyes pontja felett egy olyan z koordinátájú pontot ábrázolunk, melynek z koordinátája F(x,y).
2) Szintvonalak. Az R2  R ill. R3
R ill. R3  R típusú függvények másik ábrázolási módja a szintvonalakkal és szintfelületekkel történő ábrázolás. Példák:
R típusú függvények másik ábrázolási módja a szintvonalakkal és szintfelületekkel történő ábrázolás. Példák:
- Domborzati térkép. A térkép minden pontjához hozzá van rendelve, hogy milyen magasan van az adott hely, így ez egy R2
 R típusú függvény. Az azonos magasságú pontok (igaz csak 10 vagy 100 méterenként) görbével vannak összekötve:
R típusú függvény. Az azonos magasságú pontok (igaz csak 10 vagy 100 méterenként) görbével vannak összekötve:
- Térbeli hőtérkép. Mondjuk egy szobában van egy radiátor. A radiátor körül nagy a hőmérséklet. Egy tágabb gömbfelületen már kevesebb, a szoba átellenes pontján még kisebb. A térben az azonos hőmérsékletű pontok felületet rajzolnak ki.
3) Térgörbére vegyünk egy henger és egy gömb alkalmas metszetét, melyet a
ábra mutat és amely a
függvény által van meghatározva.
Topologikus alapfogalmak
Metrika és norma
Rn-ben értelmezzük két pont euklidészi távolságát (ez az euklideszi metrika). Ha a és b az Rn két tetszőleges pontja, akkor
Azt is mondhatjuk, hogy definiálunk egy általános vektorhosszat, amit euklidészi normának nevezünk:
majd vesszük a különbség hosszát távolságnak:
Az már a matematikusokra tartozik, hogy absztrakt módon definiálják a metrika és a norma fogalmát és belátják, hogy tetszőleges p pozitív számra
szintén norma (p=2-re az euklidészi). Hasznos sokszor a szuprémum vagy maximumnorma is:
Nyílt, zárt és kompakt halmazok
Az u ∈ Rn pont ε sugarú gömbi környezetén értjük a
halmazt ||.||2 az euklideszi normát jelenti, ekkor egy gömb R3-ban tényleg gömb lesz.
Folytonosság
Azt mondjuk, hogy az Rn egy A részhalmazán értelezett és Rm-be ható f leképezés folytonos az értelmezési tartománya egy a ∈ A pontjában
Itt ||x-a|| az x-a Rn-beli euklideszi normája, ||f(x)-f(a)|| pedig az f(x)-f(a) Rm-beli euklideszi normája.
- 1. feladat: Igazoljuk, hogy az
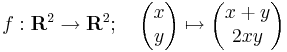
leképezés folytonos a 0 pontban.
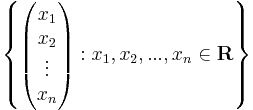
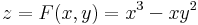
![f:[-2\pi,2\pi]\to\mathbf{R}^3;\quad t\mapsto\begin{pmatrix}1+\cos t\\ \sin t\\ 2\sin\left(\frac{1}{2}t\right)\end{pmatrix}](/upload/math/a/1/b/a1b13849fc54d335b56a736e1128a6c2.png)