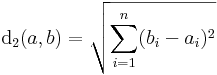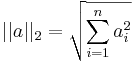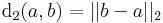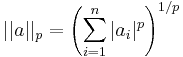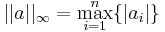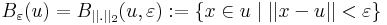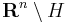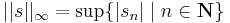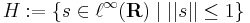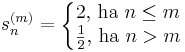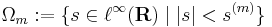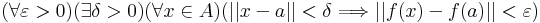Matematika A2a 2008/1. gyakorlat
Mozo (vitalap | szerkesztései) (→Bolzano-Weierstrass-tételkör) |
Mozo (vitalap | szerkesztései) (→Bolzano-Weierstrass-tételkör) |
||
| 74. sor: | 74. sor: | ||
:<math>H:=\{s\in\ell^{\infty}(\mathbf{R})\mid ||s||\leq 1\}</math> | :<math>H:=\{s\in\ell^{\infty}(\mathbf{R})\mid ||s||\leq 1\}</math> | ||
"gömb" nem kompakt. Minden egyes m természetes számre legyen az s<sup>(m)</sup> sorozat a következő: | "gömb" nem kompakt. Minden egyes m természetes számre legyen az s<sup>(m)</sup> sorozat a következő: | ||
| − | :<math>s^{(m)}_n=\left\{\begin{matrix}2\mbox{, ha }n\leq m\\\frac{1}{2}\mbox{, ha }n> m\end{matrix}</math> | + | :<math>s^{(m)}_n=\left\{\begin{matrix}2\mbox{, ha }n\leq m\\\frac{1}{2}\mbox{, ha }n> m\end{matrix}\right.</math> |
ez egy olyan függvénysorozat (igaziból sorozatsorozat, ún. kettős indexű sorozat), mely egy jobbra haladó "hullámfrontot" formáz, 2 és 1/2 a fornt előtti és utáni magasság. Világos, hogy a | ez egy olyan függvénysorozat (igaziból sorozatsorozat, ún. kettős indexű sorozat), mely egy jobbra haladó "hullámfrontot" formáz, 2 és 1/2 a fornt előtti és utáni magasság. Világos, hogy a | ||
:<math>\Omega_m:=\{s\in\ell^{\infty}(\mathbf{R})\mid |s|<s^{(m)}\}</math> | :<math>\Omega_m:=\{s\in\ell^{\infty}(\mathbf{R})\mid |s|<s^{(m)}\}</math> | ||
A lap 2008. február 3., 09:07-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Az első gyakorlaton a Rn topologikus tulajdonságait beszéljük meg, különös tekintettel, az Rn egy részhalmazából Rm-be ható folytonos leképezésekre. A meghatározottság kedvéért Rn-en a
halmazt, azaz az n emeletes valós értékű oszlopvektorkat értjük. (Mások azt mondanák, hogy R saját magával vett n-szeres Descartes-szorzata, ami azonban később elfedné a "sorvektor" és az "oszlopvektor" különbséget, ami a lineéris algebra szempontjából nem kerülendő.)
Tartalomjegyzék |
Vektorfüggvények ábrázolása
- Egyelőre görbére és felületre elég a hétköznapi értelemben gondolni. Ezekkel számolni (vonal és felületi intagrál) csak az A3-ba fogunk.
Rn  Rm függvények két legjellegzetesebb, legjobban szemléltethető típusa az
Rm függvények két legjellegzetesebb, legjobban szemléltethető típusa az
- R2
 R típusú felületek (kétváltozós, számértékű) és az
R típusú felületek (kétváltozós, számértékű) és az
- R
 R3 típusú tér- vagy R
R3 típusú tér- vagy R  R2 típusú síkgörbék (egyváltozós, vektorértékű).
R2 típusú síkgörbék (egyváltozós, vektorértékű).
Persze ezek is csak akkor személetesek, ha viszonlag egyszerűek (mondjuk polinomiálisak vagy elemi függvényekből vannak összerakva) vagy kevéssé változtatják a függvényérékeiket (simák).
1) Példa R2  R ábrázolására az
R ábrázolására az
egyenletű majomnyereg felület:
Itt az [xy] sík minden egyes pontja felett egy olyan z koordinátájú pontot ábrázolunk, melynek z koordinátája F(x,y).
2) Szintvonalak. Az R2  R ill. R3
R ill. R3  R típusú függvények másik ábrázolási módja a szintvonalakkal és szintfelületekkel történő ábrázolás. Példák:
R típusú függvények másik ábrázolási módja a szintvonalakkal és szintfelületekkel történő ábrázolás. Példák:
- Domborzati térkép. A térkép minden pontjához hozzá van rendelve, hogy milyen magasan van az adott hely, így ez egy R2
 R típusú függvény. Az azonos magasságú pontok (igaz csak 10 vagy 100 méterenként) görbével vannak összekötve:
R típusú függvény. Az azonos magasságú pontok (igaz csak 10 vagy 100 méterenként) görbével vannak összekötve:
- Térbeli hőtérkép. Mondjuk egy szobában van egy radiátor. A radiátor körül nagy a hőmérséklet. Egy tágabb gömbfelületen már kevesebb, a szoba átellenes pontján még kisebb. A térben az azonos hőmérsékletű pontok felületet rajzolnak ki.
3) Térgörbére vegyünk egy henger és egy gömb alkalmas metszetét, melyet a
ábra mutat és amely a
függvény által van meghatározva.
Topologikus alapfogalmak
Metrika és norma
Rn-ben értelmezzük két pont euklidészi távolságát (ez az euklideszi metrika). Ha a és b az Rn két tetszőleges pontja, akkor
Azt is mondhatjuk, hogy definiálunk egy általános vektorhosszat, amit euklidészi normának nevezünk:
majd vesszük a különbség hosszát távolságnak:
Az már a matematikusokra tartozik, hogy absztrakt módon definiálják a metrika és a norma fogalmát és belátják, hogy tetszőleges p pozitív számra
szintén norma (p=2-re az euklidészi). Hasznos sokszor a szuprémum vagy maximumnorma is:
Nyílt és zárt halmazok
Az u ∈ Rn pont ε sugarú gömbi környezetén értjük a
halmazt ||.||2 az euklideszi normát jelenti, ekkor egy gömb R3-ban tényleg gömb lesz.
u belső pontja H-nak, ha van olyan (gömbi) környezete u-nak, mely teljes egészében H-beli. H nyílt halmaz, ha minden pontja belső pont. H zárt, ha komplementere, azaz az
halmaz nyílt.
Világos, hogy Rn nyílt halmaz, így ennek komplementere, az üres halmaz zárt. Ám, az üres halmaz nyílt is, hiszen minden pontja belső pont. Ha ugyanis lenne olyan pontja, ami nem belső pontja, akkor lenne egyáltalán pontja, ami lehetetlen, lévén az üres halmaz üres. Így komplementere, azaz Rn zárt halmaz is. Tanulság: vannak nyílt-zárt halmazok (clopen in English) és vannak se nem nyílt, se nem zárt halmazok, például a [0,1) intervallum. Vagyis "a halmaz nem ajtó, ami vagy nyílt, vagy zárt"!
Véges sok nyílt halmaz metszete nyílt, akármennyi nyílt halmaz uniója nyílt. A zártakra a duális állítás igaz: véges sok zárt halmaz uniója zárt, akárhány zárt halmaz metszete zárt. Adjunk végtelen ellenpéldákat!
Bolzano-Weierstrass-tételkör
Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine-Borel-tétel. Korlátos és zárt halmaz kompakt.
Sorozatkompakt egy K halmaz, ha minden benne haladó sorozatból kiválasztható K-beli határértékű konvergens részsorozat.
Bolzano-Weierstrass-tétel. Korlátos és zárt halmaz sorozatkompakt.
Rn-ben tehát a kompaktság ugyanaz, mint a sorozatkompaktság.
Bolzano-Weierstrass-féle kiválasztási tétel. Korlátos sorozatnak van konvergens részsorozata.
Ha még azt a tényt is hozzávesszük, hogy egy H halmaz pontosan akkor zárt, ha minden benne haladó konvergens sorozatnak a határértéke is benne van, akkor világos, hogy mi a kapcsolat a két utóbbi tétel között.
Rn véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 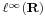 a korlátos sorozatok tere. A téren a norma a suprémum:
a korlátos sorozatok tere. A téren a norma a suprémum:
Ekkor a
"gömb" nem kompakt. Minden egyes m természetes számre legyen az s(m) sorozat a következő:
ez egy olyan függvénysorozat (igaziból sorozatsorozat, ún. kettős indexű sorozat), mely egy jobbra haladó "hullámfrontot" formáz, 2 és 1/2 a fornt előtti és utáni magasság. Világos, hogy a
halmazok nyíltak és uniójuk lefedik H-t. Ám, akárhány sok véges ilyen halmazt veszünk, biztos, hogy a H-beli konstans 1 sorozatot nem fedi le. Konstruálható H-ban haladó (korlátos), de konvergens részsorozattal nem rendelkező sorozat is. Mutassunk ilyet!
Folytonosság
Azt mondjuk, hogy az Rn egy A részhalmazán értelezett és Rm-be ható f leképezés folytonos az értelmezési tartománya egy a ∈ A pontjában
Itt ||x-a|| az x-a Rn-beli euklideszi normája, ||f(x)-f(a)|| pedig az f(x)-f(a) Rm-beli euklideszi normája.
- 1. feladat: Igazoljuk, hogy az
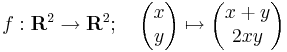
leképezés folytonos a 0 pontban.
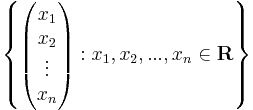
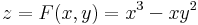
![f:[-2\pi,2\pi]\to\mathbf{R}^3;\quad t\mapsto\begin{pmatrix}1+\cos t\\ \sin t\\ 2\sin\left(\frac{1}{2}t\right)\end{pmatrix}](/upload/math/a/1/b/a1b13849fc54d335b56a736e1128a6c2.png)